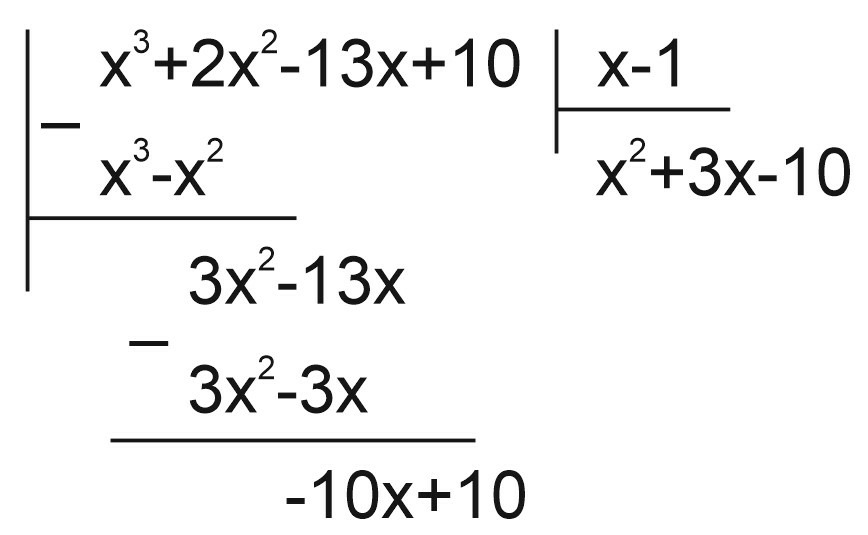ЕГЭ-2022 Вариант 6, решения

Видеоразбор: https://www.youtube.com/watch?v=vHRkJiQvnIw\&t=11679s

Часть 1. Задания с кратким ответом

1. Анна Малкова В прямоугольном треугольнике АВС катеты АС и ВС равны $\sqrt{6}$ и $2\sqrt{3}$ соответственно. Найдите высоту, проведенную к гипотенузе.

Решение:

По теореме Пифагора найдем гипотенузу треугольника АВС: ${AB}^2={AC}^2+{BC}^2\Rightarrow AB=\sqrt{{\left(\sqrt{6}\right)}^2+{\left(2\sqrt{3}\right)}^2}=\sqrt{6+12}=\sqrt{18}$

Найдем высоту, проведенную к гипотенузе, через площадь треугольника

$S_{\triangle ABC}=\displaystyle \frac{1}{2}AC\cdot BC=\displaystyle \frac{1}{2}AB\cdot h\Rightarrow$

$h=\displaystyle \frac{AC\cdot BC}{AB}=\displaystyle \frac{2\sqrt{3}\cdot \sqrt{6}}{\sqrt{18}}=\displaystyle \frac{2\sqrt{18}}{\sqrt{18}}=2$

Ответ: 2

2. Анна Малкова

Найдите объем детали, изображенной на рисунке, если диаметр основания цилиндра равен 10, высота равна $\displaystyle \frac{4}{\pi }$ , а диаметр цилиндрического отверстия равен 4.

Решение:

Так как диаметр основания равен 10, его радиус равен 5. Радиус цилиндрического отверстия равен 2.

Объем цилиндра V = $\pi R^2h$ .

Мы видим, что из большого цилиндра вырезан меньший, и объем детали равен

$V = \pi R^2h- \pi r^2h=\ \pi h\left(5^2-2^2\right)=\pi \frac{4\cdot 21}{\pi}=84$ .

Разделив на $\pi$ , получим ответ.

Ответ: 84

3. Арлен Близаров

Каждый вечер Хуан Гарсия играет на гитаре под окном неприступной красавицы Сесилии Кончиты. Вероятность того, что она в знак любви бросит ему красную розу, равна 0,1 в отдельно взятый вечер. Какие шансы, что Хуан Гарсия завоюет сердце Сесилии Кончиты, если её соседи согласны терпеть его бренчание только четыре вечера?

Решение:

Вероятность получить красную розу в отдельно взятый вечер равна 0,1. Хуан Гарсия, если повезет, получит ее в первый вечер. Тогда он приглашает Кончиту на свидание и больше под окном не бренчит. Хуан Гарсия может получить красную розу во второй, в третий или в четвертый вечер, причем вероятности каждого из этих событий разные.

Вероятность того, что Хуан Гарсия так и не добился взаимности Сесилии Кончиты, равна

$P_1=0,9\cdot 0,9\cdot 0,9\cdot 0,9=0,6561.$

Вычитая из единицы это число, получим вероятность благоприятного исхода для Хуана Гарсии: $1-0,6561=0,3439.$

Ответ: 0,3439

4. Татьяна Сиротина

Барон Мюнхгаузен в 80% случаев рассказывает небылицу. Если его рассказ — выдумка, то в 60% случаев ему не верят. А, если его рассказ правдив, то ему верят в 95% случаев.

Однажды Барон рассказал историю о том, как он первый раз влюбился. Слушатели не поверили. С какой вероятностью эта история была правдой? Ответ округлите до сотых.

Решение:

Ситуация, при которой слушатели не поверят Барону Мюнхгаузену, может сложиться в результате следующих событий: рассказ действительно небылица и слушатели не поверили рассказчику или рассказ — правда, но слушатели не поверили.

Вероятности этих событий равны соответственно $0,8\cdot 0,6=0,48\$ и $0,2\cdot 0,05=0,01.$

События «слушатели поверили Барону Мюнхгаузену» и «слушатели ему не поверили» образуют полную группу (они несовместны, и одно из них непременно происходит), поэтому можно применить формулу полной вероятности. Получим: $P=0,48+0,01=0,49$

Вероятность того, что слушатели не поверили Барону Мюнхгаузену, равна 0,49. Это мы нашли в пункте (а).

Обозначим за х вероятность того, что рассказ Мюнхгаузена о его первой влюбленности был правдив при условии, что слушатели ему не поверили.

Тогда 0,49 х — вероятность того, что слушатели не поверили, но при этом рассказ был правдой.

С другой стороны, эта вероятность равна $0,2\cdot 0,05$ . Получим: $0,2\cdot 0,05=0,49x;\ \ x=\displaystyle \frac{1}{49}\ \approx 0,02.$

Ответ: 0,02

5. Татьяна Сиротина

Решите уравнение:

${\left(\displaystyle \frac{1}{2}\right)}^{-x^2-\displaystyle \frac{3}{2}}=\displaystyle \frac{\sqrt{2}}{4^x}$

Решение:

$2^{x^2+\displaystyle \frac{3}{2}}=2^{-2x+\displaystyle \frac{1}{2}}$

$x^2+\displaystyle \frac{3}{2}=-2x+\displaystyle \frac{1}{2}$

$x^2+2x+1=0$

${\left(x+1\right)}^2=0$

$x=-1$

6. Анна Малкова

Вычислите: $\sqrt{{1013}^2-16{\cdot 253}^2}$

Решение:

Применяем формулу разности квадратов $a^2-b^2=\left(a-b\right)\cdot \left(a+b\right)$

$\sqrt{{1013}^2-16\cdot {253}^2}=\sqrt{{1013}^2-{\left(4\cdot 253\right)}^2}=$

$=\sqrt{\left(1013-1012\right)\left(1013+1012\right)}=\sqrt{2025}=45$

Ответ: 45

7. Анна Малкова

Прямая $y=7x+b$ касается графика функции $f\left(x\right)=2x^3-x^2+3x-4$ , причем абсцисса точки касания положительна. Найдите b.

Запишем условие касания:

$\left\{ \begin{array}{c}f\left(x\right)=kx+b \\f$

$\left\{ \begin{array}{c}2x^3-x^2+3x-4=7x+b \\6x^2-2x+3=7 \end{array}\right.$

Начнем со второго уравнения

$6x^2-2x-4=0$

$D=b^2-4ac=4+4\cdot 6\cdot 4=4\cdot 25={10}^2x_{1,2}=\displaystyle \frac{-b\pm \sqrt{D}}{2a}=\displaystyle \frac{2\pm 10}{12}$

$x_1=1;\ \ x_2=-\displaystyle \frac{2}{3}$

Т.к. $x_0\textgreater 0$ , то $x_0=1$ .

Найдем $b,$ подставив $x_0\$ в первое уравнение:

$2x^3-x^2+3x-4=7x+b,$ отсюда

$b=-7.$

Ответ: -7.

8. ФИПИ

Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием $f=30\$ см.

Расстояние $d_1$ от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние $d_2$ от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение $\displaystyle \frac{1}{d_1 }+\displaystyle \frac{1}{d_2 }=\displaystyle \frac{1}{f}$ Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.

Решение:

Фокусное расстояние линзы известно. Но какое же значение $d_2$ (расстояние от линзы до экрана) надо подставлять в формулу? Нам надо найти наименьшее расстояние от лампочки до линзы $d_1$ . Если $d_1$ — наименьшее, то обратная величина $\displaystyle \frac{1}{d_1}$ будет наибольшей. Поскольку $\displaystyle \frac{1}{f}$ — константа, второе слагаемое $\displaystyle \frac{1}{d_2\ }\$ в формуле линзы должно быть наименьшим, а обратная ему величина $d_2$ — наибольшей, то есть равной 180. Подставим данные в формулу:

$\displaystyle \frac{1}{d_1}+\displaystyle \frac{1}{180}=\displaystyle \frac{1}{30},$

$d_1=36.$

Ответ: 36.

9. Александра Антонова

Василий поссорился с Машей, и они с одинаковыми скоростями пошли по улице в противоположных направлениях. Через 10 минут Василий повернул назад и, увеличив скорость в три раза, стал догонять Машу (чтобы помириться). Через сколько минут Василий догнал Машу?

Решение:

Пусть x — скорости Василия и Маши, когда они двигались в противоположных направлениях. За 10 минут расстояние между Василием и Машей стало равно 10x + 10x = 20x.

Затем Василий повернул назад со скоростью 3x. За время, равное t, Василий смог догнать Машу. Составим таблицу:

	v	t	S
Маша	x	t	xt
Василий	3x	t	3xt

С того момента, как Василий повернул назад, до момента их встречи Василий прошел на 20х больше, чем Маша, то есть $3xt-xt=20x.\$

Отсюда $2xt=20x,\; t=10$ минут.

Ответ: 10.

10. Графики функций $\ f\left(x\right)=3{\left(x+1\right)}^2$ и g(x) пересекаются в точках А и В. По данным рисунка найдите абсциссу точки В.

Решение:

Запишем формулу функции $y=g(x)$ .

Ее график — квадратичная парабола $g\left(x\right)=a_{\ }x^2+b_{\ }x+c_{\ };$

$g\left(-2\right)=3;$

$g\left(-4\right)=-5,$ то есть

$\left\{ \begin{array}{c}a_{\ }\cdot {\left(-2\right)}^2+b_{\ }\cdot \left(-2\right)+c_{\ }=3 \\a_{\ }\cdot {\left(-4\right)}^2+b_{\ }\cdot \left(-4\right)+c_{\ }=-5 \end{array}\right.$

$\left\{ \begin{array}{c}4a_{\ }-2b_{\ }+c_{\ }=3 \\16a_{\ }-4b_{\ }+c_{\ }=-5 \end{array}\right.$

Вычитаем из первого уравнения второе:

$-12a_{\ }+2b_{\ }=8,$ то есть.

$-6a_{\ }+b_{\ }=4.$

Так как $x=-4$ — абсцисса вершины параболы,

$-\displaystyle \frac{b_{\ }}{2a_{\ }}=-4,$

$b_{\ }=8a_{\ .}$

Получим:

$\left\{ \begin{array}{c}-6a_{\ }+8a_{\ }=4 \\b_{\ }=8a_{\ } \end{array}\right.$

$\left\{ \begin{array}{c}a_{\ }=2 \\b_{\ }=16 \end{array}\right.$

Подставив в уравнение $4a_{\ }-2b_{\ }+c_{\ }=3,$ получаем:

$8-32+c_{\ }=3;$

$c_{\ }=27.$

Значит, $y=2x^2+16x+27.$

Найдем точки пересечения графиков $f(x)$ и $g(x)$ .

Для этих точек: $f\left(x\right)=g(x)$

$3x^2+6x+3=2x^2+16x+27;$

$x^2-10x-24=0;$

$D=100+96=196;$

$\sqrt{D}=14$

$x=-2$ или $x=12.$

Абсцисса точки A равна -2 (как и показано на рисунке). Тогда абсцисса точки B равно 12.

Ответ: 12.

11. Найдите наименьшее значение функции $y=3{cos x-\pi x+\pi ^2\ }$ на отрезке $\left[-2\pi ;\ \pi \right]$ .

Решение:

$y$

$y$ ; $-3{sin x\ }=\pi \Leftrightarrow \ \ {sin x\ }=-\displaystyle \frac{\pi }{3}\ \Leftrightarrow x\in \emptyset$ , так как $-\displaystyle \frac{\pi }{3}\textless -1$

$-3{sin x\ }-\pi \textless 0$ при любом x, то есть $y$ , а это означает, что $y\left(x\right)$ - убывает, наименьшее значение функции достигается в правом конце отрезка $\left[-2\pi ;\ \pi \right]$ .

$y_{min}=y\left(\pi \right)=-3$

Ответ: -3

Часть 2. Задания с развернутым ответом

12. Анна Малкова

а) Решите уравнение: $2{{sin^3 x\ }}^{\ }-5{sin x+3=cos^2 x\ }$

б) Найдите все его корни на отрезке [-3 $\pi$ ; 1]

Решение:

Из основного тригонометрического тождества: ${cos}^2x=1-{sin}^2x$ .

$2sin^3x -5sinx+3=1-{sin}^2x$

Замена: $sinx=t;\ \ \left|t\right|\le 1$

$2t^3+t^2-5t+2=0.$

Разложим левую часть на множители.

Подберем целый корень уравнения среди делителей свободного члена, то есть среди делителей числа 2.

Целые делители числа 2 — это $\pm 1;\pm 2.$

$t=1$ подходит.

$t=1$ — корень уравнения $2t^3+t^2-5$ $t+2=0.$

Это означает, что многочлен $2t^3+t^2-5t+2$ делиться на $\left(t-1\right)$ без остатка.

Можно разделить уголком:

или можно вынести $\left(t-1\right)$ за скобки.

$2t^3+t^2-5t+2=2t^3-2t^2+3t^2-3t-2t+2=$

$=2t^2\left(t-1\right)+3t\left(t-1\right)-2\left(t-1\right)=\left(t-1\right)\left(2t^2+3t-2\right)$

Получили: $\left(t-1\right)\left({2t}^2+3t-2\right)=0\Leftrightarrow \left(t-1\right)\left(t-0,5\right)\left(t+2\right).$

$t=-2\ \$ - не подходит т.к. $\left|t\right|\le 1$ .

Получили: $\left[ \begin{array}{c}t=1 \\t=0,5 \end{array}\right.$ .

Вернемся к переменной $x.$

$\left[ \begin{array}{c}sinx=1 \\sinx=\displaystyle \frac{1}{2} \end{array}\right.$

Получили: $\displaystyle \frac{\pi }{2}+2\pi k;\ \ \displaystyle \frac{\pi }{6}+2\pi k;\ \displaystyle \frac{5\pi }{6}+2\pi k;\ k\in Z.$

$\left[ \begin{array}{c}x=\displaystyle \frac{\pi }{2}+2\pi k \\x=\displaystyle \frac{\pi }{6}+2\pi k \\x=\displaystyle \frac{5\pi }{6}+2\pi k \end{array}\ k\in Z\right.$

б). Отберём корни уравнения на отрезке $\left[-3\pi ;1\right]$ c помощью единичной окружности. Для этого отметим на единичной окружности данный отрезок и найденные серии решений.

Нарисуем две окружности. На одной отметим отрезок $\left[-3\pi ;-\pi \right]$ , на другой $\left[-\pi ;1\right]$ .

Вспомним, что 1рад = $57{}^\circ \textgreater \displaystyle \frac{\pi }{6}$ .

Мы видим, что отрезку $\left[-3\pi ;1\right]$ принадлежат корни:

$x_1=-2\pi +\displaystyle \frac{\pi }{6}=-\displaystyle \frac{11\pi }{6}; x_2=-2\pi +\displaystyle \frac{\pi }{2}=-\displaystyle \frac{3\pi }{2}$

$x_3=-2\pi +\displaystyle \frac{5\pi }{6}=-\displaystyle \frac{7\pi }{6}; x_4=\displaystyle \frac{\pi }{6} .$

Ответ: а) $\displaystyle \frac{\pi }{2}+2\pi k;\ \ \displaystyle \frac{\pi }{6}+2\pi k;\ \displaystyle \frac{5\pi }{6}+2\pi k;\ k\in Z\ \ \$

б) $-\displaystyle \frac{11\pi }{6}$ ; $\ -\displaystyle \frac{3\pi }{2};-\displaystyle \frac{7\pi }{6};\ \ \displaystyle \frac{\pi }{6}\ .\ \ \ \ \$

13. Анна Малкова

В треугольной пирамиде АВСS с вершиной S боковые ребра равны 12, углы АSB и ВSC равны 45 ${}^\circ$ , угол ASC равен 60 ${}^\circ$ .

Точки Е, F, K лежат на ребрах AS, BS, CS так, что SE = 6, SF = 8, SK = 4.

а) Докажите, что плоскость EFK делит пирамиду на многогранники, объемы которых относятся как 1 : 8.

б) Найдите угол между плоскостями SFE и SFK. Ответ запишите в градусах.

Решение:

$SABC$ - треугольная пирамида, в которой боковые ребра $SA=SB=SC=12$

$AE=ES=6$ т.е. E — середина SA

$\ SF\ =\ 8\Rightarrow FB=4.$

$\ SK\ =\ 4\Rightarrow KC=8.$

Плоскость $\left(EFK\right)$ отрезает от пирамиды «верхушку», и нужно найти отношение объемов полученных частей.

Воспользуемся формулой:

$\displaystyle \frac{V_{SEFK}}{V_{SABC}}=\displaystyle \frac{SE}{SA}\cdot \displaystyle \frac{SF}{SB}\cdot \displaystyle \frac{SK}{SC}=\displaystyle \frac{1}{2}\cdot \displaystyle \frac{8}{12}\cdot \displaystyle \frac{4}{12}=\displaystyle \frac{1}{9}\Rightarrow$

$V_{SEFK}=\displaystyle \frac{1}{9}V_{SABC}\Rightarrow V_{ABCKFE}=\displaystyle \frac{8}{9}V_{SABC}\Rightarrow$

$\displaystyle \frac{V_{SEFK}}{V_{ABCKFE}}=\displaystyle \frac{1}{8}.$

Докажем формулу, с помощь которой нашли это отношение:

Треугольники $SEF$ и $SAB$ имеют по равному углу $\varphi$ , отношение их площадей равно:

$\displaystyle \frac{S_{\triangle SEF}}{S_{\triangle SAB}}=\displaystyle \frac{\displaystyle \frac{1}{2}\cdot SE\cdot SF\cdot sin\varphi }{\displaystyle \frac{1}{2}\cdot SA\cdot SB\cdot sin\varphi }=\displaystyle \frac{SE}{SA}\cdot \displaystyle \frac{SF}{SB}.$

По формуле объема пирамиды,

Пусть h — расстояние от точки $K$ до плоскости $\left(SEF\right)$ .

Пусть $KK_1$ — перпендикуляр из точки К на плоскость $\left(SEF\right).$

$h=KK_1$ — высота пирамиды $SEFK$ , в основании которой лежит $\triangle SEF$ .

Построим прямую $SK_1$ в плоскости $\left(SAB\right)$ .

$SK_1$ - проекция $SK$ на $\left(SAB\right)$ .

Точка С лежит на прямой $SK$ . Тогда её проекция будет лежать на прямой $SK_1$ .

Точка $C_1$ — проекция точки С на плоскость $\left(SAB\right)$ , $C_1\in SK_1,$ значит,

$CC_1\bot \left(SAB\right).\$

Получили:

$\left. \begin{array}{c}KK_1\bot \left(\ SAB\right) \\CC_1\bot \left(SAB\right) \end{array}\right]\Rightarrow CC_1\parallel KK_1.$

Мы получили подобные треугольники.

$\triangle SKK_1\sim \triangle SCC_1$ по двум углам, $\displaystyle \frac{KK_1}{CC_1}=\displaystyle \frac{SK}{SC}$ .

$V_{SABC}=\displaystyle \frac{1}{3}S_{\triangle SAB}\cdot CC_1$

$V_{SEFK}=\displaystyle \frac{1}{3}S_{\triangle SEF}\cdot KK_1$

$\displaystyle \frac{V_{SEFK}}{V_{SABC}}=\displaystyle \frac{\displaystyle \frac{1}{3}S_{\triangle SEF}\cdot KK_1}{\displaystyle \frac{1}{3}S_{\triangle SAB}\cdot CC_1}=\displaystyle \frac{SE}{SA}\cdot \displaystyle \frac{SF}{SB}\cdot \displaystyle \frac{KK_1}{CC_1}=\displaystyle \frac{SE}{SA}\cdot \displaystyle \frac{SF}{SB}\cdot \displaystyle \frac{SK}{SC}$ , что и требовалось доказать.

б). Найдем угол между плоскостями $\left(SFE\right)$ и $\left(SFK\right).\$ Это то же самое, что угол между плоскостями $\left(SAB\right)$ и $\left(SBC\right)$ .

$\triangle SAB=\triangle SBC$ по двум сторонам и углу.

Построим $AH\bot SB$ , соединим $H$ и $C$ .

$\triangle ASH=\triangle CSH$ по двум сторонам и углу. Отсюда $AH=HC,$ значит,

$\angle SHC=90{}^\circ .$

Получили, что $CH\$ — высота $\triangle SBC$ ,

тогда $\angle AHC$ — угол между плоскостями $\ \left(SAB\right)$ И $\left(SBC\right)$ .

$\triangle AHC;$ $AC=12,$ так как $\triangle ASC$ правильный.

$\triangle SAH$ — прямоугольный и равнобедренный $\Rightarrow$

$AH=\displaystyle \frac{12}{\sqrt{2}} .$

$AH=CH=\displaystyle \frac{12}{\sqrt{2}}\ ;\ \ AC=12\ \Rightarrow \triangle AHC$ - равнобедренный и прямоугольный, для него выполняется теорема Пифагора. Получили $\angle H=90{}^\circ$

Ответ: $90{}^\circ$

14. ФИПИ

Решите неравенство:

${{log}_3 \displaystyle \frac{1}{x}\ }+{{log}_3 \left(x^2+3x-9\right)\le {{log}_3 \left(x^2+3x+\displaystyle \frac{1}{x}-10\right).\ }\ }$

Решение.

${{log}_3 \displaystyle \frac{1}{x}\ }+{{log}_3 \left(x^2+3x-9\right)\le {{log}_3 \left(x^2+3x+\displaystyle \frac{1}{x}-10\right)\Leftrightarrow \left\{ \begin{array}{c}x\textgreater 0 \\x^2+3x-9\textgreater 0 \\x^2+3x+\displaystyle \frac{1}{x}-10\textgreater 0 \\0\textless \displaystyle \frac{x^2+3x-9}{x}\le \displaystyle \frac{x^3+3x^2-10+1}{x} \end{array}\right.\ }\ }$

(третье неравенство следует из остальных)

$\Leftrightarrow \left\{ \begin{array}{c}x\textgreater 0 \\x^2+3x-9\textgreater 0 \\x^2+3x-9\le x^3+3x^2-10x+1 \end{array}\Leftrightarrow \left\{ \begin{array}{c}x\textgreater 0 \\x^2+3x-9\textgreater 0 \\x^3+2x^2-13x+10\ge 0 \end{array}\Leftrightarrow \left\{ \begin{array}{c}x\textgreater 0 \\x^2+3x-9\textgreater 0 \\\left(x-1\right)\left(x-2\right)\left(x+5\right)\ge 0 \end{array}\right.\right.\right.$

$x^3+2x^2-13x+10=\left(x-1\right)\left(x-2\right)\left(x+5\right)$

$x=1$ корень

3 неравенства с учётом $x\textgreater 0:$

$\Leftrightarrow \left\{ \begin{array}{c}\left[ \begin{array}{c}0\textless x\le 1 \\x\ge 2 \end{array}\right. \\\left[ \begin{array}{c}x\textless \displaystyle \frac{-3-3\sqrt{5}}{2} \\x\textgreater \displaystyle \frac{3\sqrt{5}-3}{2} \end{array}\right. \end{array}\right.$
$\displaystyle \frac{3\sqrt{5}-3}{2}\textgreater 1;\displaystyle \frac{3\sqrt{5}-3}{2}\textless 2$

Ответ: $\left[2;\ +\infty \right)$

15. В 2015 году Федор взял в кредит сумму S на 6 лет под 25% годовых, причем вначале банк начисляет проценты, затем Федор переводит в банк определенную сумму денег. По условиям кредита, в 2016, 2017, 2018 и 2019 годах после очередной выплаты сумма долга ежегодно уменьшается на 1/10 первоначальной величины, выплаты 2020 и 2021 годов равны. Всего Федор выплатил 250 тысяч рублей. Найдите S.

Решение:

Составим схему погашения кредита в 2016 — 2019 годах

Первые выплаты:

$z_1=kS-0,9S$

$z_2=0,9kS-0,8S$

$z_3=0,8kS-0,7S$

$z_4=0,7kS-0,6S$

Сумма выплат за 4 года:

$z_1+z_2+z_3+z_4=kS\left(1+0,9+0,8+0,7\right)-S\left(0,9+0,8+0,7+0,6\right)=$

$=kS\cdot 3,4-3S$

$k=1+\displaystyle \frac{p}{100}=1,25=\displaystyle \frac{5}{4}$

$z_1+z_2+z_3+z_4=S\cdot \left(3,4\cdot \displaystyle \frac{5}{4}-3\right)=S\cdot \left(\displaystyle \frac{17}{4}-3\right)=\displaystyle \frac{5}{4}S$

Пусть выплаты 2020 и 2021 года равны x

$\left(0,6kS-x\right)\cdot k-x=0$

$0,6k^2S-x\left(k+1\right)=0$

$x=\displaystyle \frac{0,6k^2S}{k+1}=\displaystyle \frac{3\cdot 4\cdot 25}{5\cdot 9\cdot 16}\cdot S=\displaystyle \frac{5}{12}S$

Выплаты за 2020 и 2021 годы: $2x=\displaystyle \frac{5}{6}S$

Всего выплачено:

$B=\left(\displaystyle \frac{5}{4}+\displaystyle \frac{5}{6}\right)S=\displaystyle \frac{5}{2}\left(\displaystyle \frac{1}{2}+\displaystyle \frac{1}{3}\right)S=\displaystyle \frac{25}{12}S$

$\displaystyle \frac{25}{12}S=250$ тыс.рублей

S=120 тыс. рублей

Ответ: 120 тыс. рублей

16. ФИПИ

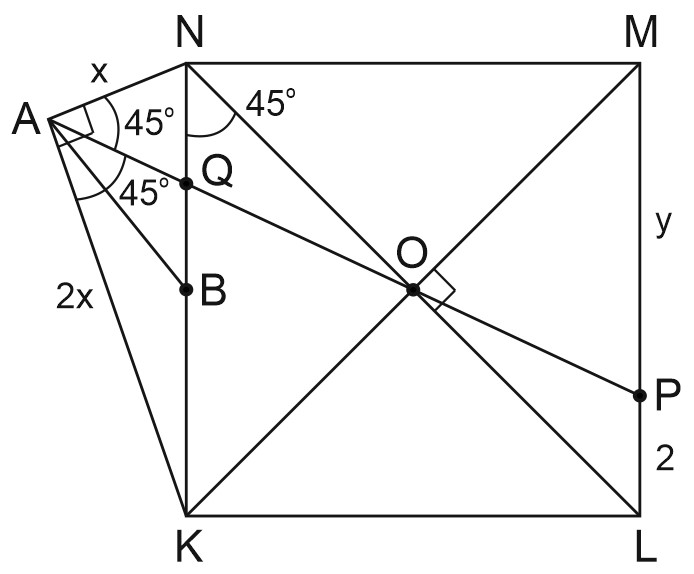
Точка A расположена вне квадрата KLMN с центром O, причём треугольник KAN прямоугольный ( $\angle A=90^\circ$ ) и AK=2AN. Точка B — середина стороны KN.

а) Докажите, что прямая BM параллельна прямой AN.

б) Прямая AO пересекает сторону ML квадрата в точке P, LP = 2. Найдите PM.

Решение:

Дан квадрат $KLNM$ и прямоугольный треугольник $KAN$ .

$\angle A=90{}^\circ ; AK=2AN.$

Точка В — середина $KN$ .

Докажем, что $BM\parallel AN$ .

Точка В — середина $KN\Rightarrow NM=2KB,AK=2AN$ , поэтому $\triangle KAN\sim \triangle MNB$ по прямому углу и двум сторонам.

Отсюда $\angle ANB=\angle NBM$ как соответственные,

Рассмотрим прямые $AN$ и $BM$ и секущую $BN$ .

$\angle ANB=\angle NBM$ - накрест лежащие, значит

$\Rightarrow AN\parallel BM$ , что и требовалось доказать.

б) $AO\cap ML$ =P, LP=2. Найдем PM.

О — точка пересечения диагоналей квадрата $KLNM,$

$\triangle ONK$ прямоугольный и равнобедренный.

$\angle O=90{}^\circ ,\ \angle ONK=45{}^\circ .\$

Четырехугольник $ANOK$ можно вписать в окружность, так как

$\angle A+\angle O=90{}^\circ +90{}^\circ =180{}^\circ .$

Пусть $Q=AO\cap NK,$

$\angle ONK=\angle OAK$ — вписанные, опираются на дугу OK.

$\angle ONK=\angle OAK=45{}^\circ \Rightarrow \angle QAN=90{}^\circ -45{}^\circ =45{}^\circ ,$

$\left. \begin{array}{c}\angle OAK=45{}^\circ \\\angle QAN=45{}^\circ \end{array}\right\}\Rightarrow$ AQ - биссектриса $\triangle KAN$

По свойству биссектрисы угла треугольника,

$\displaystyle \frac{NQ}{KQ}=\displaystyle \frac{1}{2}=\displaystyle \frac{AN}{AK}\Rightarrow KQ=2NQ.$

$\triangle QON=\triangle POL$ (по стороне и двум углам),

$PL=NQ=2, QK=4$

$\triangle QOK=\triangle POM\Rightarrow PM=4.$

Ответ: 4

17. МГУ

При каких значениях параметра а система уравнений

$\left\{ \begin{array}{c}y^2-\left(2a+1\right)y+a^2+a-2=0 \\\sqrt{{\left(x-a\right)}^2+y^2}+\sqrt{{\left(x-a\right)}^2+{\left(y-3\right)}^2}=3 \end{array}\right.$

имеет единственное решение?

Решение:

Решим систему графически в координатах $\left(x;y\right).$

Первое уравнение:

$y^2-\left(2a+1\right)y+a^2+a-2=0;$ раскроем скобки и сгруппируем слагаемые.

$y^2-2ay-y+a^2+a-2=0\Leftrightarrow {\left(y-a\right)}^2-\left(y-a\right)-2=0$

Замена $y-a=z$ ,

$z^2-z-2=0\Leftrightarrow \left[ \begin{array}{c}z=2 \\z=-1 \end{array}\right.$ .

Вернемся к переменный а и у.

$\left[ \begin{array}{c}y-a=2 \\y-a=-1 \end{array}\right.\Leftrightarrow \left[ \begin{array}{c}y=a+2 \\y=a-1 \end{array}\right.$

График первого уравнения — две горизонтальные прямые, расстояние между которыми равно 3.

Второе уравнение — это уравнение отрезка.

Вспомним, что уравнение вида

$\sqrt{{\left(x-a\right)}^2+{\left(x-b\right)}^2}+\sqrt{{\left(x-c\right)}^2+{\left(y-d\right)}^2}=\sqrt{{\left(c-a\right)}^2+{\left(d-b\right)}^2}$ задает отрезок $\left[MN\right].$ Здесь $P\left(x;y\right)$ — любая точка этого отрезка,

$M\left(a;b\right)$ и $N\left(c;d\right)$ - концы отрезка. В нашем случае

$\sqrt{{\left(x-a\right)}^2+y^2}+\sqrt{{\left(x-a\right)}^2+{\left(y-3\right)}^2}=3$

Концы отрезка — точки $A\left(a;0\right)$ и $B\left(a;3\right).$

Второе уравнение задает множество отрезков $\left[AB\right]$ , двигающихся вдоль оси $X$ параллельно оси Y, длиной $\left|AB\right|=3$ .

Система имеет единственное решение, если только одна из горизонтальных прямых $y=a+2;\ \ y=a-1$ пересекает отрезок, а другая прямая не пересекает.

Возможны случаи:

$\left[ \begin{array}{c}\left\{ \begin{array}{c}0\le a-1\le 3 \\a+2\textgreater 3 \end{array}\right. \\\left\{ \begin{array}{c}0\le a+2\le 3 \\a-1\textless 0 \end{array}\right. \end{array}\Leftrightarrow \right.\left[ \begin{array}{c}\left\{ \begin{array}{c}1\le a\le 4 \\a\textgreater 1 \end{array}\right. \\\left\{ \begin{array}{c}-2\le a\le 1 \\a\textless 1 \end{array}\right. \end{array}\Leftrightarrow \right.\left[ \begin{array}{c}1\textless a\le 4 \\-2\le a\textless 1 \end{array}\right.$

Ответ: $a\in [-2;1)\cup (1;4]$ .

18. Студент Василий выбирает для Маши букет в День Святого Валентина. Красная роза стоит 220 рублей, розовая 190 рублей. Василий хочет, чтобы число розовых и красных роз в букете отличалось не больше, чем на 3. Всего у Василия с собой 2900 рублей.

а) Может ли Василий купить для Маши 11 роз?

б) Может ли Василий купить букет из 15 роз?

в) Какое наибольшее количество роз может быть в букете, если это число нечетно?

Решение

Вопросы пунктов а), б) и в) похожи. Поэтому сделаем «заготовку» сразу для всех пунктов задачи.

Пусть x — количество красных роз, y - количество розовых. Тогда

$\ 220x+190y\le 2900$

$22x+19y\le 290$

Число красных роз отличается от числа розовых не больше, чем на 3. Значит,

$| y - x | \leq 3$ , то есть $-3\le y-x\le 3.$

Мы получили систему неравенств

$\left\{ \begin{array}{c}22x+19y\le 290, \\-3\le y-x\le 3 \end{array}\right.$

В каждом из пунктов (а), (б) и (в) задается вопрос о том, сколько всего роз можно купить в данных условиях. Обозначим k = x + y — число роз. Выразим отсюда y = k — x и получим систему неравенств с переменными х и k.

$\left\{ \begin{array}{c}19k+3x\le 290, \\\displaystyle \frac{k-3}{2}\le x\le \displaystyle \frac{k+3}{2} \end{array}\right.$

а) Пусть k = 11. Получим: $\left\{ \begin{array}{c}x\le 27, \\\ 4\le x\le 7, \end{array}\right.$ можно.

Пример: Возьмем x = 7 и y = 4. Букет будет стоить 2300 рублей.

б) Пусть k = 15. Получим: $\left\{ \begin{array}{c}3x\le 5, \\\ 6\le x\le 9. \end{array}\right.$

Эта система не имеет решений. Значит, 15 роз Василий не купит.

в) Мы получили, что 11 роз купить можно, а 15 нельзя, причем число роз нечетно. Проверим, можно ли купить букет из 13 роз.

При k = 13 получим: $\left\{ \begin{array}{c}x\le 14 \frac{1}{3}, \\\ 5\le x\le 8. \end{array}\right.$ , так как $x \in Z$ , то $\left\{\begin{matrix}x\leq 14\\ 5\leq x \leq 8\end{matrix}\right.$

Возьмем x = 8, y =5.

Букет будет стоить: $8 \cdot 220 + 5 \cdot 190 = 2710$ рублей.

Ответ:

а) да

б) нет

в) 13

Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «ЕГЭ-2022 Вариант 6, решения» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена: 06.03.2023

ЕГЭ-2022 Вариант 6, решения

Это полезно