Часть 1. Задания с кратким ответом
Видеоразбор: https://www.youtube.com/watch?v=lFgpirr4MRI\&t=10s
1. Александра Антонова
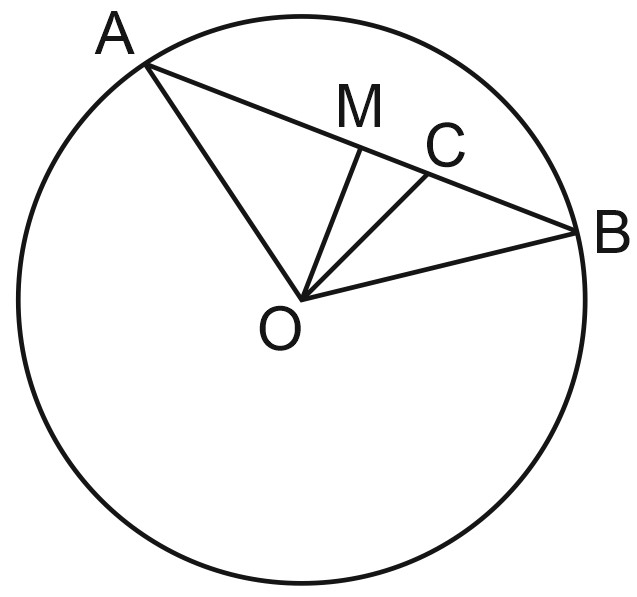
В окружности точка С делит хорду на два отрезка длиной 7 см и 8 см. Найдите расстояние от точки С до центра окружности, если радиус окружности равен 9 см.
Решение:
Пусть \(M\) - середина хорды \(AB,\)
\(\triangle AOB\) равнобедренный, тогда \(OM\bot AB.\)
Треугольники \(AOM\) и \(COM\) прямоугольные,
\(OM\) - их общий катет.
Выразим \(OM\) из обоих треугольников:
\({OM}^2={AO}^2-{AM}^2={OC}^2-{CM}^2,\)
\(AB=8+7=15;\ \ AM=\displaystyle \frac{15}{2}=BM;\ \ CM=\displaystyle \frac{1}{2};OC=x;\)
\(81-{\left(\displaystyle \frac{15}{2}\right)}^2=x^2-{\left(\displaystyle \frac{1}{2}\right)}^2\Leftrightarrow x^2=25;\ x=5.\)
Ответ: 5
2. Анна Малкова
Найдите объем усеченного конуса, высота которого равна \(\displaystyle \frac{8}{\pi }\), радиус большего основания равен 9, радиус меньшего основания равен 3.
Решение:
Достроим усеченный конус до обыкновенного конуса, продлив его образующие. Объем усеченного конуса найдем как разницу объемов большого и маленького конусов.
Пусть \({SO}_1=x\ \) - высота маленького конуса, \(SO_2=H=\) \(x+\displaystyle \frac{8}{\pi }-\ \) высота большого конуса.
\(\triangle SO_1A\sim \triangle SO_2B;\ \ \)
\(\ \displaystyle \frac{{SO}_1}{SO_2}=\displaystyle \frac{r}{R};\)
\(\displaystyle \frac{x}{x+\displaystyle \frac{8}{\pi }}=\displaystyle \frac{3}{9}=\displaystyle \frac{1}{3};\)
\(3x=\displaystyle \frac{8}{\pi }+x;\ \ x=\displaystyle \frac{4}{\pi }\) — высота меньшего конуса.
Объем усеченного конуса найдем как разность двух конусов.
\(V=V_1-V_2=\displaystyle \frac{\pi }{3}\left(R^2H-r^2h\right)=\displaystyle \frac{\pi }{3}\left(81\cdot \displaystyle \frac{12}{\pi }-9\cdot \displaystyle \frac{4}{\pi }\right)=\)
\(=\displaystyle \frac{9\cdot 4}{3}\left(9\cdot 3-1\right)=12\cdot 26=312.\)
Ответ: 312
3. Анна Малкова Перед 8 марта кондитерская «Тортец», находящаяся в городе N, надеется увеличить продажи тортов, для чего дает рекламу на городском телеканале, в газете города N и на сайте объявлений города.
Известно, что рекламу на телеканале увидят 10% жителей города N, рекламу на сайте объявлений — 20% жителей, а рекламу в газете увидят 5% жителей города. С какой вероятностью житель города N увидит рекламу кондитерской «Тортец»?
Решение:
Житель города увидит рекламу кондитерской на телевидении с вероятностью 0,1, а не увидит с вероятностью 0,9. Аналогично, житель не увидит рекламу «Тортеца» в газете с вероятностью 0,95 и не увидит рекламу в интернете с вероятностью 0,8.
Найдем вероятность того, что житель города N не увидит рекламу кондитерской «Тортец» ни на телеканале, ни в газете, ни в интернете. Считая, что эти события независимы, находим произведение вероятностей: \(p_1 = 0,9 \cdot 0,95 \cdot 0,8 = 0,684.\)
Противоположное событие — житель увидит рекламу кондитерской по телевизору, в газете или на сайте. Вероятность этого события \(p = 1 - p_1 = 1 - 0,684 = 0,316.\)
Ответ: 0,316
4. Татьяна Сиротина
Стрелок делает 5 выстрелов по мишени. Вероятность попадания при одном выстреле равна 0,5. Найдите вероятность того, что мишень будет поражена более двух, но менее пяти раз. Результат округлите до сотых.
Решение: Используем формулу Бернулли \(P^n_m=C^n_m\cdot p^nq^{m-n}\)
В данном случае: \(n=5\) — количество выстрелов,
\(p=0,5\) — вероятность поражения мишени при каждом выстреле;
\(q =1-p\)=1-0,5 = 0,5\) — вероятность промаха при каждом выстреле,
m=3 или m=4 — число попаданий. По теореме сложения вероятностей несовместных событий:
\(P_5\left(2\textless m\textless 5\right)=P^3_5+P^4_5=C^3_5{\left(0,5\right)}^3\cdot {\left(0,5\right)}^2+C^4_5{\left(0,5\right)}^4\cdot {\left(0,5\right)}^1=\)
\(=\displaystyle \frac{5!}{3!\left(5-3\right)!}\cdot {\left(0,5\right)}^5+\displaystyle \frac{5^!}{4!\left(5-4\right)!}\cdot {\left(0,5\right)}^5=\)
\(=\displaystyle \frac{4\cdot 5}{2}\cdot {\left(0,5\right)}^5+\displaystyle \frac{5}{1}\cdot {\left(0,5\right)}^5=\displaystyle \frac{10}{32}+\displaystyle \frac{5}{32}=\displaystyle \frac{15}{32}\approx 0,47.\)
Мы нашли вероятность того, что при 5 выстрелах мишень будет поражена более двух, но менее пяти раз.
Ответ: 0,47.
5. Решите уравнение:\(\ \ \ \ \ \displaystyle \frac{2x-3}{7x-3}=\ \displaystyle \frac{2x-3}{13x+4}\)
Если уравнение имеет несколько корней, в ответе запишите больший из них.
Перенесем все в левую часть уравнения и вынесем общий множитель за скобки:
\(\displaystyle \frac{2x-3}{7x-3}-\displaystyle \frac{2x-3}{13x+4}=0\Leftrightarrow \left(2x-3\right)\cdot \left(\displaystyle \frac{1}{7x-3}-\displaystyle \frac{1}{13x+4}\right)=0\Leftrightarrow \)
Произведение двух множителей равно нулю, тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл.
Уравнение равносильно системе:
\(\Leftrightarrow \left\{ \begin{array}{c}
\left[ \begin{array}{c}
2x=3 \\
7x-3=13x+4 \end{array}
\right. \\
7x-3\ne 0 \\
13x+4\ne 0 \end{array}
\right.\Leftrightarrow \left[ \begin{array}{c}
x=1,5 \\
x=-\displaystyle \frac{7}{6} \end{array}
\right.\)
Нам нужен больший корень, а это \(x=1,5\)
Ответ: 1,5
6. Анна Малкова
Вычислите: \(\displaystyle \frac{7 cos \left ( \frac{3 \pi}{2} -x \right ) - 2 sin \left ( -5 \pi - x \right )}{sin \left ( 2022 \pi +x \right )}.\)
Решение:
Воспользуемся формулами приведения.
\(cos\left(\displaystyle \frac{3\pi }{2}-x\right)=-sinx,\)
\(sin\left(-5\pi -x\right)=sinx,\)
\(sin\left(2022\pi +x\right)=sinx.\)
\(\displaystyle \frac{7 cos \left ( \frac{3 \pi}{2} -x \right ) - 2 sin \left ( -5\pi - x \right )}{sin \left ( 2022 \pi +x \right )}=\frac{-7sin x -2 sin x}{sin x}=\frac{-9sinx}{sin x}=-9\)
Ответ: -9
7. Анна Малкова
На рисунке изображён график функции \(y\ =\ F(x)\) — одной из первообразных функции \(f(x),\) определённой на интервале \((-11;\ 11).\)
Найдите количество точек, принадлежащих интервалу \((-11;\ 11)\), в которых функция \(y\ =\ f(x)\) меняет знак с положительного на отрицательный.
Решение:
Так как \(f(x)\) — производная функции \(F(x)\), ее знак меняется с «+» на «минус» в точках максимума функции F(x). Таких точек на интервале \((-\ 11;\ 11)\) семь.
Ответ: 7
8. ФИПИ
Два тела массой m = 2 кг каждое, движутся с одинаковой скоростью v = 10 м/с под углом друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением \(mv^2 sin^2 \alpha \geq 100.\). Под каким наименьшим углом (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 100 джоулей?
Решение:
По условию, \(Q \geq 100\) Дж, то есть \(mv^2 sin^2 \alpha \geq 100.\)
Подставив данные из условия, получим: \(200 sin^2 \alpha \geq 100;\)
Отсюда \(\displaystyle sin ^2 \alpha \geq \frac{1}{2}\)
В ответе нужно записать наименьший угол \(2 \alpha \).
По формуле понижения степени, \({{sin}^2 a=\displaystyle \frac{1-cos2a}{2}\ }\)
Значит, \(1 - cos 2\alpha \geq 1\)
\(cos 2\alpha \leq 0.\)
Согласно условию, \(0{}^\circ \ \le \ 2\alpha \ \le 180{}^\circ \ \)
Наименьший угол \(2\alpha \) на этом отрезке, для которого \(cos\ 2\alpha \ \le \ 0\), это угол \(2\alpha \ =\ 90{}^\circ \), так как
\(cos\ 90{}^\circ \ =\ 0. \)
Ответ: 90
9. Анна Малкова
Из пункта А выехал автомобиль «Ока». В тот же момент из пункта В навстречу ему выехал автомобиль «Пежо» со скоростью на 35 км/ч большей, чем у «Оки», и через 5 часов проехал мимо «Оки». Через час после выезда «Оки» из пункта А стартовал автомобиль «Лада Калина» со скоростью на 4 км/ч большей, чем у «Оки», и достиг пункта В одновременно с «Окой». Найдите скорость автомобиля «Ока». Ответ выразите в км/ч.
Решение:
Пусть x км/ч — скорость «Оки», x + 35 км/ч — скорость «Пежо».
Расстояние между городами:
\(S=x\cdot 5+\left(x+35\right)\cdot 5\)
\(x+4\) — скорость «Лады Калины».
Составим таблицу:
| V | t | S | |
| Ока | x | 5 | \(5x=S_1\) |
| Пежо | x+35 | 5 | \(5(x+35)=S_2\) |
| Лада Калина | x+4 | \(\displaystyle \frac{S}{x+4}\) | \(S=S_1+S_2\) |
\(\displaystyle t=\frac{S}{V}\) часов. Так как «Лада Калина» прошла все расстояние АВ на один час быстрее «Оки», то получим уравнение \(\displaystyle \frac{S}{x}-1=\frac{S}{x+4}\) часов.
Мы получили 2 уравнения:
\(\left\{ \begin{array}{c}
S=x\cdot 5+\left(x+35\right)\cdot 5 \\
\displaystyle \frac{S}{x}-\displaystyle \frac{S}{x+4}=1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{array}
\right.\)
Подставили S в первое уравнение.
\(5\cdot \left(2x+35\right)\cdot \left(\displaystyle \frac{1}{x}-\displaystyle \frac{1}{x+4}\right)=1\)
\(5\left(2x+35\right)\cdot \displaystyle \frac{4}{x\left(x+4\right)}=1\)
\(20\left(2x+35\right)=x\left(x+4\right)\)
\(40x+700=x^2+4x\)
\(x^2-36x-700=0;\)
\(D=4^2\left(81+175\right)=16\cdot 256.\)
\(x=\displaystyle \frac{36\pm 64}{2}\), \(x\textgreater 0\), \(x=50\) км/ч.
Ответ: 50.
10. ФИПИ
На рисунке изображён график функции вида \(f\left(x\right)=\displaystyle \frac{x^2}{a}+bx+c,\ \)где числа a, b и c — целые. Найдите значение \(f\left(13\right).\)
Решение:
\(f\left(x\right)=\displaystyle \frac{x^2}{a}+bx+c\)
Запишем формулу функции в более привычном виде:
\(f\left(x\right)=a_1x^2+bx+c\), где \(a_1=\displaystyle \frac{1}{a};\ \ \ \ \ a_1\textless 0\), так как ветви параболы направлены вниз.
Вершина параболы в точке \(\left(6;8\right).\)
График функции получен из графика функции \(y=a_1x^2\) сдвигом на 6 единиц вправо и на 8 единиц вверх, т.е.
\(f\left(x\right)=a_1{\left(x-6\right)}^2+8.\)
\(f\left(0\right)=-1\), тогда \(36a_1+8=-1;\ a_1=-\displaystyle \frac{1}{4}\) .
Получили \(f\left(x\right)=-\displaystyle \frac{1}{4}\ \ {\left(x-6\right)}^2+8\).
\(f\left(13\right)=-\displaystyle \frac{1}{4}\ \ {\left(13-6\right)}^2+8=-\displaystyle \frac{1}{4}\ \ \cdot 49+8=8-\displaystyle \frac{49}{4}=-4,25\)
Ответ: -4,25
11. ФИПИ
Найдите наибольшее значение функции \(y=-\displaystyle \frac{2}{3}x\sqrt{x}+3x+1\ \) на отрезке \(\left[1;9\right].\)
Решение:
Преобразуем формулу функции:
\(y=-\displaystyle \frac{2}{3}x\sqrt{x}+3x+1 =-\displaystyle \frac{2}{3}\cdot x^{\displaystyle \frac{3}{2}}+3x+1.\)
\(y'\left(x\right)=-\displaystyle \frac{2}{3}\cdot \displaystyle \frac{3}{2}\cdot x^{\displaystyle \frac{1}{2}}+3=3-\sqrt{x} ;\)
\(y'=0;\ 3-\sqrt{x}=0;\ \ \sqrt{x}=3;\ x=9.\)
Наибольшее значение функции на отрезке достигается в точке максимума или на конце отрезка.
Исследуем знаки производной:
При x \(\textless \) 9 производная положительна, а это означает, что функция монотонно возрастает на отрезке [1; 9] и наибольшее значение принимает в правом конце отрезка, то есть при \(x=9\).
Значит, \(y_{max}=y\left(9\right)=-\displaystyle \frac{2}{3}\cdot 9\sqrt{9}+3\cdot 9+1=10.\)
Ответ: 10.
Часть 2. Задания с развернутым ответом
12. а) Решить уравнение:
\(3{\ sin}^3x-4{sin x+2\sqrt{3}\ }=2\sqrt{3}{cos}^2x\)
б) Найти все корни на промежутке \(\left[0;\ \displaystyle \frac{\pi }{2}\right]\).
Решение.
Так как \({cos}^2x\ \)= 1-\({sin}^2x\), получим:
\(3{\ sin}^3x-4{sin x+2\sqrt{3}\ }=2\sqrt{3\ }(1-{sin}^2x),\)
\(3{\ sin}^3x+2\sqrt{3\ }{sin}^2x-4{sin x\ }=0,\)
\((3{\ sin}^2x+2\sqrt{3\ }{sin x\ }-4){sin x\ }=0,\)
Сделаем замену \({sin x\ }=t\), \(\left|t\right|\le 1\).
Решим систему \(\ \left\{ \begin{array}{c}
(3t^2+2\sqrt{3\ }t-4)t=0, \\
\left|t\right|\le 1 \end{array}
\right.\ \) \(\left\{ \begin{array}{c}
\left[ \begin{array}{c}
3t^2+2\sqrt{3\ }t-4=0\ \\
t=0 \end{array}
\right. \\
\left|t\right|\le 1 \end{array}
\right.\).
Решим уравнение
\(3t^2+2\sqrt{3\ }t-4=0\ .\)
\(\displaystyle \frac{D}{4}=3+12=15, \ \left[ \begin{array}{c}
t=-\displaystyle \frac{1+\sqrt{5}}{\sqrt{3}} \\
t=\displaystyle \frac{-1+\sqrt{5}}{\sqrt{3}} \end{array}
\right.. \)
Вернемся к системе:
\(\left\{ \begin{array}{c}
\left[ \begin{array}{c}
t=-\displaystyle \frac{1+\sqrt{5}}{\sqrt{3}} \\
t=\displaystyle \frac{-1+\sqrt{5}}{\sqrt{3}} \\
t=0 \end{array}
\right. \\
\left|t\right|\le 1 \end{array}
\right..\)
Так как \(-\displaystyle \frac{1+\sqrt{5}}{\sqrt{3}}\textless \ -1\), значит, \(t=-\displaystyle \frac{1+\sqrt{5}}{\sqrt{3}}\ \)не подходит. Получим:
\(\ \left[ \begin{array}{c}
t=\displaystyle \frac{\sqrt{5\ }-1}{\sqrt{3}} \\
t=0 \end{array}
\right.\)
\(\left[ \begin{array}{c}
{sin x\ }=\displaystyle \frac{\sqrt{5\ }-1}{\sqrt{3}} \\
{sin x\ }=0 \end{array}
\right., \left[ \begin{array}{c}
x={arcsin \displaystyle \frac{\sqrt{5\ }-1}{\sqrt{3}}\ +2\pi k,\ k\in Z\ } \\
x=\pi -{arcsin \displaystyle \frac{\sqrt{5\ }-1}{\sqrt{3}}+2\pi m,\ m\in Z\ } \\
x=\pi n,\ n\in z \end{array}
\right..\)
б) Отберём корни уравнения на отрезке \([0;\ \displaystyle \frac{\pi }{2}]\) c помощью единичной окружности. Для этого отметим на ней данный отрезок и найденные серии решений.
Видим, что данному отрезку принадлежат точки:
\(x_1=0\)
\(x_2=arcsin\left(\displaystyle \frac{\sqrt{5}-1}{\sqrt{3}}\right).\)
Ответ: а)\(\ arcsin\left(\displaystyle \frac{\sqrt{5}-1}{\sqrt{3}}\right)+2\pi k;\ \pi -arcsin\left(\displaystyle \frac{\sqrt{5}-1}{\sqrt{3}}\right)+2\pi k;\ k\in Z;\ \pi m;\ \ m\in Z\ \)
б) 0; \(arcsin\left(\displaystyle \frac{\sqrt{5}-1}{\sqrt{3}}\right)\)
13. В основании прямой призмы ABCA\({}_{1}\)B\({}_{1}\)C\({}_{1}\) лежит равнобедренный прямоугольный треугольник ABC с гипотенузой AB, равной 8√2. Высота призмы равна 6.
а) Докажите, что плоскость, содержащая прямую AC\({}_{1}\) и параллельная прямой CB\({}_{1}\) проходит через середину ребра A\({}_{1}\)B\({}_{1}\).
б) Найдите косинус угла между прямыми AC\({}_{1}\) и CB\({}_{1}\).
Решение:
\(ABCA_1B_1C_1\) - прямая призма,
\(\triangle ABC\) - равнобедренный,
\(AB=8\sqrt{2}\Rightarrow AC=BC=8.\)
Высота \(AA_1=6.\)
Плоскость сечения \(\alpha ,\ \ AC_1\in \alpha ;\ \alpha \parallel CB_1\).
\(M\) - середина \(A_1B_1\)
Докажем, что \(M\in \alpha .\)
Достроим призму \(ABCA_1B_1C_1\) до прямоугольного параллелепипеда.
\(AE_1\parallel CB_1\Rightarrow \left(AC_1E_1\right)\parallel CB_1\) по признаку параллельности прямой и плоскости.
\(\left(AC_1E_1\right)\cap A_1B_1=M\)
\(A_1C_1B_1E_1\) — квадрат, тогда середина \(A_1B_1\), что и требовалось доказать.
б) Найдем \(,\) где \(\varphi \) — угол между прямыми \(AC_1\) и \(CB_1.\)
Прямые \(AC_1\) и \(CB_1\) скрещивающиеся, \(\varphi =\angle C_1AE_1\) т.к. \(AE_1\parallel CB_1.\)
Найдем \(\angle C_1AE_1\) из \(\triangle C_1AE_1.\)
Из \(\triangle ACC_1:\ \ \ AC=8;\ \ CC_1=6;\ \ \angle C=90{}^\circ \Rightarrow AC_1=10\) по теореме Пифагора.
\(\triangle AEE_1=\triangle ACC_1\Rightarrow AE_1=10,\)
Из \(\triangle A_1C_1E_1\\) получим: \(\ C_1E_1=8\sqrt{2}\).
По теореме косинусов для \(\triangle AC_1E_1\):
\({C_1E_1}^2={AC_1}^2+{AE_1}^2-2AC_1\cdot AE_1\cdot {cos \varphi },\)
\(128=100+100-200{cos \varphi \Rightarrow {\ {cos \varphi =\displaystyle \frac{9}{25} } }} ,\)
\(\varphi =arccos\displaystyle \frac{9}{25}.\)
Ответ: \(\displaystyle \frac{9}{25}\).
14. Александра Антонова
Решите неравенство:
\({log}_3\left(3^x-1\right)\cdot {log}_{\displaystyle \frac{1}{3}}\left(3^{x+1}-3\right)\textgreater -2\)
\({{log}_3 \left(3^x-1\right)\cdot {{log}_{\displaystyle \frac{1}{3}} \left(3^{x+1}-3\right)\textgreater -2\ }\ }\)
Решение:
\(3^x=t;t\textgreater 0\)
\({{log}_3 \left(t-1\right)\cdot {{log}_{\displaystyle \frac{1}{3}} \left(3t-3\right)\textgreater -2\ }\ }\)
\({{log}_3 \left(t-1\right)\cdot {{log}_3 \left(3t-3\right)\textless 2\ }\ }\)
\(log_3 (t-1)\cdot (log_3 (t-1)+1)-2 \textless 0\)
\({{log}_3 \left(t-1\right)=y;\ }\)
\(y\left(y+1\right)-2\textless 0\)
\(y^2+y-2\textless 0\)
\(\left(y+2\right)\left(y-1\right)\textless 0\)
\(\displaystyle \frac{1}{9}\textless t-1\textless 3\)
\(\displaystyle \frac{10}{9}\textless t\textless 4;\)
\(\displaystyle \frac{10}{9}\textless 3^x\textless 4;\)
\({{log}_3 \displaystyle \frac{10}{9} \textless x\textless {{log}_3 4\ }\ }\)
Ответ: \(({log}_3\displaystyle \frac{10}{9};{log}_34)\)
15. Александра Антонова
В июле 2022 года Григорий планирует взять кредит в банке на 2,5 млн рублей. Условия его возврата такие:
- в январе 2023, 2024, 2025, 2026, 2027 годов долг возрастает на 12% по сравнению с концом предыдущего года;
- в январе 2028, 2029, 2030, 2031, 2032 годов долг возрастает на r % по сравнению с концом предыдущего года;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- к июлю 2032 года долг должен быть полностью погашен;
Чему равно r, если общая сумма выплат составит 4 млн рублей?
Решение:
Введем обозначения.
Срок кредита n= 10 лет,
Сумма кредита S=2,5 млн. руб.,
Сумма выплат B = 4 млн. руб.
В 2023 — 2027 годы 12% - процент банка, k=1,12 — коэффициент ежегодного увеличения долга после начисления процентов.
В 2028 — 2032 годы r%- процент банка\(,\ q=\left(1+\displaystyle \frac{r}{100}\right)\ \ \)— коэффициент ежегодного увеличения долга после начисления процентов.
Найдем r.
Кредит погашается по схеме с дифференцированными платежами и равномерным уменьшением суммы долга.
Выплаты:
\(y_1=Sk-\displaystyle \frac{9}{10}S;\)
\(y_2=\displaystyle \frac{9}{10}Sk-\displaystyle \frac{8}{10}S;\)
\(y_3=\displaystyle \frac{8}{10}Sk-\displaystyle \frac{7}{10}S;\)
\(y_4=\displaystyle \frac{7}{10}Sk-\displaystyle \frac{6}{10}S ;y_5=\displaystyle \frac{6}{10}Sk-\displaystyle \frac{5}{10}S; y_6=\displaystyle \frac{5}{10}Sq-\displaystyle \frac{4}{10}S;\)
\(y_7=\displaystyle \frac{4}{10}Sq-\displaystyle \frac{3}{10}S;\)
\(y_8=\displaystyle \frac{3}{10}Sq-\displaystyle \frac{2}{10}S;\)
\(y_9=\displaystyle \frac{2}{10}Sq-\displaystyle \frac{1}{10}S;\)
\(y_{10}=\displaystyle \frac{1}{10}Sq.\)
Общая сумма выплат: \(B=y_1+y_2+y_3+\dots +y_{10}=\)
\(=\displaystyle \frac{Sk}{10}\left(10+9+8+7+6\right)+\displaystyle \frac{Sq}{10}\left(5+4+3+2+1\right)-\displaystyle \frac{S}{10}\left(9+8+\dots +1\right)=\)
\(=\displaystyle \frac{Sk}{10}\cdot 40+\displaystyle \frac{Sq}{10}\cdot 15-\displaystyle \frac{S}{10}\cdot 45=4Sk+1,5Sq-4,5S,\)
\(1,5Sq=B+4,5S-4Sk,q=\displaystyle \frac{B+4,5S-4Sk}{1,5S}=\)
\(=\displaystyle \frac{B}{1,5S}+\displaystyle \frac{4,5-4k}{1,5}=\displaystyle \frac{4\cdot 2\cdot 2}{3\cdot 5}+\displaystyle \frac{9-8\cdot 1,12}{3}=\displaystyle \frac{16}{15}+\displaystyle \frac{0,04}{3}=\)
\(=\displaystyle \frac{16}{15}+\displaystyle \frac{4}{300}=\displaystyle \frac{16}{15}+\displaystyle \frac{1}{75}=\displaystyle \frac{81}{75}=\displaystyle \frac{27}{25}=1,08\), тогда r = 8%.
Ответ: 8%
16. Анна Малкова
В остроугольном треугольнике АВС угол В больше, чем угол А. Точка М — середина стороны АС, точка О — центр окружности, описанной вокруг треугольника АВС, СН — высота.
а) Докажите, что треугольники АОМ и СВН подобны.
б) Известно, что в треугольнике АВС углы А, В и С относятся как 3 : 4 : 5. Луч СО пересекает сторону АВ в точке L, причем BL = \(\sqrt{6\ }\). Найдите CL.
Решение:
\(\triangle ABC\) - остроугольный, \(\angle B\textgreater \angle A,\)
M - середина AC,
O - центр описанной около треугольника АВС окружности,
OM - серединный перпендикуляр к AC,
Пусть \(OM\) пересекает окружность в точке K.
\(\angle \)AOC - центральный,
\(\angle ABC\) — вписанный, \(\angle ABC=\displaystyle \frac{1}{2}\breve{AKC}\).
\(OM\bot AC\Rightarrow OM\) - высота равнобедренного \(\triangle AOC\).
OM - биссектриса \(\angle AOC\Rightarrow \angle AOM=\displaystyle \frac{1}{2}\angle AOC=\displaystyle \frac{1}{2}\breve{AKC}\)
Значит, \(\left. \begin{array}{c}
\angle ABC=\angle AOM \\
\angle BHC=\angle OMA=90{}^\circ \end{array}
\right\}\Rightarrow \triangle AOM\sim \triangle CBH\) по двум углам.
б) \(\angle A\ :\angle B\ :\angle C=3\ :4\ :5,\ \ \ \)
\(CO\cap AB=L,\ \ \ BL=\sqrt{6}\) . Найдем CL.
Из \(\triangle ABC:\ \ \angle A+\angle B+\angle C=180{}^\circ \Rightarrow \)
\(3x+4x+5x=180{}^\circ ;\ \ x=15{}^\circ .\)
\(\angle A=45{}^\circ ;\ \ \angle B=60{}^\circ ;\ \ \angle C=75{}^\circ .\)
\(\triangle AOM\sim \triangle CBH\Rightarrow \angle B=60{}^\circ =\angle AOM=\angle MOC;\)
\(\left. \begin{array}{c}
\angle OCM=30{}^\circ \\
\angle ACB=75{}^\circ \end{array}
\right\}\Rightarrow \angle LCB=75{}^\circ -30{}^\circ =45{}^\circ .\)
По теореме синусов из \(\triangle LCB\):
\(\displaystyle \frac{LB}{{sin C\ }}=\displaystyle \frac{LC}{{sin B\ }}\Rightarrow \displaystyle \frac{\sqrt{6}}{{sin 45{}^\circ \ }}=\displaystyle \frac{LC}{{sin 60{}^\circ \ }}\Rightarrow LC=\displaystyle \frac{\sqrt{6}\cdot \sqrt{3}}{\displaystyle \frac{1}{\sqrt{2}}\cdot 2}=3\)
Ответ: 3
17. Найдите все значения параметра а, при каждом из которых система
\(\left\{ \begin{array}{c}
y\left(y+1\right)\le 0 \\
3x^2+3y^2-6a\left(x+y\right)+5a^2-6x+4a+3=0 \end{array}
\right.\)
имеет единственное решение.
Решение:
\(\left\{ \begin{array}{c}
y\left(y+1\right)\le 0 \\
3x^2+3y^2-6a\left(x+y\right)+5a^2-6x+4a+3=0 \end{array}
\right.\)
Решим систему графически в координатах \(\left(x;y\right).\)
Первое неравенство:
\(y\left(y+1\right)\le 0\Leftrightarrow -1\le y\le 0. \)
Первое неравенство задает на плоскости горизонтальную полосу между прямыми \(y=-1\) и \( y=0\) вместе с границами полосы.
Во втором уравнении выделим полные квадраты.
\(3x^2+3y^2-6a\left(x+y\right)+5a^2-6x+4a+3=0;\ \)
\(3x^2+3y^2-6ax-6ay+5a^2-6x+4a+3=0; \)
\(\left(3x^2-6ax+3a^2\right)+\left(3y^2-6ay+3a^2\right)+\left(-6x+6a\right)-a^2-\)
\(-2a+3=0.\)
Вынесем общий множитель за скобки и свернем по формулам сокращенного умножения. Получим:
\({3\left(x-a\right)}^2+3{\left(y-a\right)}^2-6\left(x-a\right)-a^2-2a+3=0.\)
Чтобы преобразования были проще, сделаем замену \(\left(x-a\right)=b.\)
Тогда \({3\left(x-a\right)}^2-6\left(x-a\right)+3={3b}^2-6b+3=3\left(b^2-2b+1\right)=\)
\(=3{\left(b-1\right)}^2=3{\left(x-a-1\right)}^2\).
Уравнение примет вид:
\({3\left(x-a-1\right)}^2+3{\left(y-a\right)}^2=a^2+2a.\ \)
Разделив обе части уравнения на 3, получим уравнение:
\({\left(x-a-1\right)}^2+{\left(y-a\right)}^2=\displaystyle \frac{a^2+2a}{3}\)
При \(a^2+2a\textgreater 0\) это уравнение задает окружность с центром в точке \(\left(a+1;a\right)\) и радиусом \(R=\sqrt{\displaystyle \frac{a^2+2a}{3}\ \ \ }\).
Так как координаты центра записаны с использованием параметра, то графиком второго уравнения является множество окружностей, двигающихся вдоль прямой.
Это происходит, когда \(a^2+2a\textgreater 0\Leftrightarrow a\left(a+2\right)\textgreater 0\Leftrightarrow \left[ \begin{array}{c}
a\textgreater 0 \\
a\textless -2 \end{array}
\right.\) .
Координаты центра каждой окружности: \(x=a+1;\ y=a\).
Другими словами, \(y=x-1\) - линия центров окружностей.
При \(a^2+2a=0\) уравнение задает точку с координатами \(x=a+1\); \(y=a.\)
Это происходит, если \(a=0\) или \(a=-2.\)
При \(a^2+2a\textless 0\) — нет решений.
Система имеет единственное решение в следующих случаях:
1)Если окружность касается сверху прямой у = 0 в точке A или снизу касается прямой у = – 1 в точке В.
2)Второе уравнение системы задает точку, лежащую в полосе \(- 1 \leq y \leq 0.\)
В случае касания в точке A расстояние от центра окружности до оси Х равно радиусу окружности.
\(\left\{ \begin{array}{c}
a\textgreater 0 \\
a^2=\displaystyle \frac{a^2+2a}{3} \end{array}
\right.;\ \)
\(\left\{ \begin{array}{c}
a\textgreater 0 \\
3a^2=a^2+2a \end{array}
\right.;\ \)
\(\left\{ \begin{array}{c}
a\textgreater 0 \\
2a^2-2a=0 \end{array}
;\ \right.\)
\(\left\{ \begin{array}{c}
a\textgreater 0 \\
\left[ \begin{array}{c}
a=0 \\
a=1 \end{array}
\right. \end{array}
\right.;\)
\(\ a=1.\)
В случае касания в точке В:
\(\left\{ \begin{array}{c}
a\textless -1 \\
{\left(a+1\right)}^2=\displaystyle \frac{a^2+2a}{3} \end{array}
\right.;\ \)
\(\left\{ \begin{array}{c}
a\textless -1 \\
{3a}^2+6a+3=a^2+2a \end{array}
\right.;\)
\(\left\{ \begin{array}{c}
a\textless -1 \\
{2a}^2+4a+3=0 \end{array}
;\right.\) решений нет, так как дискриминант квадратного уравнения отрицателен. Значит, касания в точке В не может быть.
Система также имеет единственное решение, если окружность превращается в точку и при этом лежит внутри полосы, заданной первым неравенством. Мы сказали, что это происходит при \(a=0\) или \(a=-2\).
Если \(a=0,\ \) получим точку \(C\left(1;0\right).\) Она лежит на границе полосы, заданной первым неравенством.
Если \(a=-2\), получим точку \(D\left(-1;-2\right)\). Она не принадлежит полосе.
Получили \(a=1\) и \(a=0\).
Ответ: \(a\in \left\{0;1\right\}\)
18. Множество чисел назовем хорошим, если его можно разбить на два подмножества с одинаковой суммой чисел.
а) Является ли множество {200; 201; 202; . . . ; 299} хорошим?
б) Является ли множество \(\left\{2;4;8;\dots ;2^{100}\right\}\) хорошим?
в) Сколько хороших четырёхэлементных подмножеств у множества \(\left\{1;2;4;5;7;9;11\right\}\)?
Решение.
а) Заметим, что числа \(200, 201\dots 299\) образуют арифметическую прогрессию.
Множество A = {200, 201, . . . , 299} можно разбить на 50 пар с равной суммой чисел в каждой паре: (200, 299), (201, 298), . . . , (249, 250). Числа из первых 25 пар пусть образуют множество \(A_1\), остальные числа — множество \(A_2\). Тогда A = \(A_1\) \(\cup \) \(A_2\), причём суммы чисел в подмножествах \(A_1\) и \(A_2\) равны. Следовательно, A — хорошее множество.
б) Первый способ. Заметим, что все числа множества B = {2, 4, 8, . . . , \(2^{100}\)}, кроме 2, делятся на 4. Разобьём множество B на два каких-либо подмножества. Будем считать, что число 2 находится во втором подмножестве. Тогда сумма чисел первого подмножества делится на 4, а сумма чисел второго — нет, и эти суммы не могут быть равны. Значит, множество B не является хорошим.
Второй способ. Разобьём множество B на два каких-либо подмножества. Будем считать, что число \(2^{100}\) находится в первом подмножестве. Тогда сумма чисел первого подмножества не меньше, чем \(\ 2^{100},\) а сумма чисел второго подмножества не больше, чем
2 + 4 + . . . + \(2^{99}\) = \(2^{100}\) − 2
Значит, суммы чисел в обоих подмножествах не могут быть равны, и поэтому множество B не является хорошим.
в) Множество не может быть хорошим, если сумма его чисел нечётна. Поэтому для того чтобы множество было хорошим, необходимо, чтобы оно содержало чётное количество нечётных чисел. Тогда сумма его чисел четна.
Хорошее четырёхэлементное подмножество множества M = {1, 2, 4, 5, 7, 9, 11} может содержать ровно два или четыре нечётных числа.
Значит, нам надо выбрать два числа из пяти нечётных или 4 числа из пяти нечетных.
Если вы знакомы с комбинаторикой, вы знаете, что два числа из 5 нечетных можно выбрать \(C^2_5=10\) способами.
Можно сделать это и без применения формул комбинаторики, перебором вариантов. Выпишем все возможные варианты, то есть подмножества. Всего получится десять подмножеств:
\(A_1 = \{1, 2, 4, 5\}; A_6 = \{2, 4, 5, 9\}; \)
\(A_2 = \{1, 2, 4, 7\}; A_7 = \{2, 4, 5, 11\}; \)
\(A_3 = \{1, 2, 4, 9\}; A_8 = \{2, 4, 7, 9\}; \)
\(A_4 = \{1, 2, 4, 11\}; A_9 = \{2, 4, 7, 11\}; \)
\(A_5 = \{2, 4, 5, 7\}; A_{10} = \{2, 4, 9, 11\}. \)
Проверка показывает, что хорошими являются только шесть из них: \(A_1\), \(A_2\), \(A_5\), \(A_7\), \(A_8\) и \(A_{10}\).
Обратите внимание, что перебор вариантов — не хаотичный, а упорядоченный.
Четыре числа из пяти нечётных можно выбрать \(C^4_5=5\) способами. Или, если не знакомы с комбинаторикой, просто выписать возможные подмножества. Всего 5 подмножеств:
\(B_1 = \{1, 5, 7, 9\}; \)
\(B_2 = \{1, 5, 7, 11\}; \)
\(B_3 = \{1, 5, 9, 11\}; \)
\(B_4 = \{1, 7, 9, 11\}; \)
\(B_5 = \{5, 7, 9, 11\}. \)
Хорошими являются только два из них: \(B_2\) и \(B_5\).
Получили, что множество M имеет 8 хороших четырёхэлементных подмножеств.
Ответ: а) да; б) нет; в) 8.