Видеоразбор: https://www.youtube.com/watch?v=e0ESKbjsl5o\&t=3940s
Часть 1. Задания с кратким ответом
1. Елена Любецкая
В равнобедренном треугольнике АВС на основании АВ взята произвольная точка К. Через К и вершину, противолежащую основанию, провели прямую. Радиус окружности, описанной вокруг треугольника ACK, равен 8. Найдите радиус окружности, описанной вокруг треугольника BCK.
Решение:
По теореме синусов для \(\displaystyle \triangle ACK: \ \frac{AC}{sin \angle AKC} = \frac{KC}{sin \angle CAB} =2R_1.\)
По теореме синусов для \(\displaystyle \triangle CBK: \ \frac{BC}{sin \angle CKB} = \frac{KC}{sin \angle CBA} =2R_2.\)
По условию, \(\triangle ABC\) - равнобедренный с основанием \(AB.\) Тогда \(AC=BC\) и \(\angle CAB = \angle CBA.\)
Так как \( \angle AKC + \angle CKB = 180^\circ\) как смежные, \(sin \angle AKC = sin \angle CKB.\)
Из пунктов (1) и (2) следует, что \(\displaystyle \frac{AC}{sin \angle AKC} = \frac{BC}{sin \angle CKB}.\) значит, \(R_1 = R_2 = 8.\)
Ответ: 8
2. Анна Малкова
В правильной восьмиугольной пирамиде радиус окружности, описанной вокруг основания, равен 3, высота равна \(7\sqrt{2}.\) Найдите объем пирамиды.
В основании пирамиды правильный восьмиугольник, который состоит из 8-ми равных равнобедренных треугольников.
\(\triangle AOB=\triangle BOC=\ \triangle COD=\dots =\triangle KOA\), значит, ![]()
Так как \(\angle AOB=\angle BOC=90^\circ :2=45^\circ ,\)
\(S_{\triangle AOB}=\frac{1}{2}\cdot AO\cdot BO\cdot sin45^\circ =\frac{1}{2}\cdot 3\cdot 3\cdot \frac{\sqrt{2}}{2}=\frac{9\sqrt{2}}{4} , \)
Ответ: 84
3. В лифт 11-этажного бизнес-центра на 1 этаже входят 4 человека. Предположим, что каждый из них может выйти на любом этаже, начиная со второго. Найдите вероятность того, что все они выйдут на разных этажах.
Решение:
Первый из этих людей может выйти на любом из 10 этажей (со второго до 11-го).
Для того чтобы все четверо вышли на разных этажах, необходимо, чтобы второй человек вышел на любом этаже, кроме того, на котором вышел первый. Вероятность этого события равна \(\displaystyle \frac{9}{10}.\)
Аналогично, третьему надо выйти на любом из оставшихся 8 этажей. Вероятность этого события \(\displaystyle \frac{8}{10}.\)
Для четвертного человека вероятность выйти на таком этаже, на котором не вышел никто из троих, равна \(\displaystyle \frac{7}{10}.\)
Вероятность одновременного наступления этих событий равна произведению вероятностей, то есть \(0,9\cdot \ 0,8\cdot \ 0,7=0,504.\)
Ответ: 0,504
4. Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши уже есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 2 или 3 шоколадных яйца?
Решение:
Купив шоколадное яйцо, Маша с вероятностью 0,2 найдет в нем такую же принцессу, какая у нее уже сеть (старую принцессу), а с вероятностью 0,8 — новую принцессу.
Если для получения следующей принцессы Маше придётся купить 2 шоколадных яйца, значит, в первом купленном яйце была старая принцесса, а во втором — новая.
Вероятность этого равна \(0,2\cdot 0,8=0,16.\)
Если придется купить 3 яйца, значит, в первых двух были старые принцессы, а в третьем новая.
Вероятность такого события равна \(\displaystyle\frac{2}{10}\cdot \frac{2}{10}\cdot \frac{8}{10}=0,032.\)
Значит, вероятность получить новую принцессу, купив 2 или 3 яйца, равна \(0,16+0,032=0,192.\)
Ответ: 0,192
5. Анна Малкова
Решите уравнение \(\displaystyle \frac{2}{3}x^2=-7\frac{2}{3}x.\)
Если уравнение имеет несколько корней, в ответе запишите меньший корень.
Решение:
\(\displaystyle \frac{2}{3}x^2=-7\frac{2}{3}x; \; \;\) \(\displaystyle \frac{2}{3}x^2+7\frac{2}{3}x=0; \ \ \ \ \ \\) \(\displaystyle \frac{2}{3}x^2+\frac{23}{3}x=0; \;\;\) \(\displaystyle 2x^2+23x=0;\;\)
x(2x + 23) = 0; x = 0 или x = \(-11,5.\) Меньший корень: x = -11,5.
Ответ: -11,5
6. Найдите значение выражения:
\( \displaystyle \sqrt{(\sqrt{5}-log_3 9)\cdot \left(\sqrt{5}+log_{12}144\right)}+\frac{7 cos\left(\frac{\pi}{2}+x\right)+3 cos\left(\frac{3\pi}{2}-x \right)}{sin \left(\pi - x \right)} \)
Решение:
\({log}_39=2; {log}_{12}144=2; \)
\((\sqrt{5}-2)(\sqrt{5}+2)={\left(\sqrt{5}\right)}^2-2^2=5-4=1;\)
cos(\(\ \frac{\pi }{2}+x)=-sinx\) ; cos(\(\ \frac{3\pi }{2}-x)=-sinx;\) sin(\(\pi -x)=sinx;\)
\(\displaystyle \frac{7{cos \left(\frac{\pi }{2}+x\right)\ }+3{cos \left(\frac{3\pi }{2}-x\right)\ }}{sin(\pi -x)} = \frac{-7sinx-3sinx}{sin x}=-10;\)
1 - 10 = - 9.
Ответ: -9
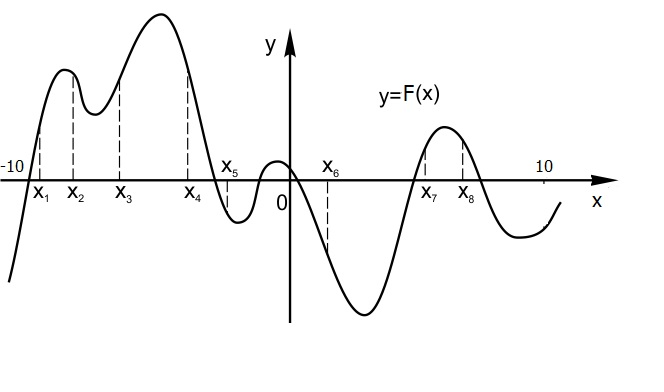
7. На рисунке изображен график F(x) — первообразной некоторой функции f(x). На оси абсцисс отмечено 8 точек: \(x_1,\ \ x_2,\ {\ x}_3,\ \ x_4,\ \ x_5,\ {\ x}_6,\ {\ x}_7,\ {\ x}_8.\) В скольких из этих точек функция f(x) принимает положительные значения? В ответ запишите количество точек.
Решение:
Так как F(x) — первообразная некоторой функции f(x), то \(f(x) = F'(x).\) Если производная функции положительна, то функция монотонно возрастает. Значит, если \(f(x)\textgreater 0,\) то F(x) монотонно возрастает. Найдем на рисунке точки, лежащие на интервалах возрастания функции F(x).
Таких точек ровно три: \(x_1, x_3\) и \( x_7.\)
Ответ: 3
8. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5.
Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
\(\displaystyle R=\frac{2In+Op+3Tr+Q}{A}.\)
Каким должно быть число A, чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1?
Решение:
Поскольку показатели максимальны, они равны 5. Подставим значения в формулу:
\(\displaystyle 1=\frac{10+5+15+5}{A}\Leftrightarrow A=35.\)
Ответ: 35
9. Александра Антонова
В городе N в 2010 г. количество детей относилось к количеству взрослых в отношении 2:3. В 2020 г. это отношение стало соответственно 5:8. Известно, что количество взрослых с 2010 по 2020 год возросло на 80%, а количество детей увеличилось на 55 тыс. Сколько человек составляло население города в 2010 г.?
Решение:
Пусть в 2010 году было x тысяч детей, а взрослых — y тысяч, тогда в 2020 году детей
стало x + 55 тыс., а взрослых 1,8y тыс. Запишем данные в таблицу:
| год | Дети (тыс. человек) | Взрослые (тыс. человек) |
| 2010 | x | y |
| 2020 | x+55 | 1,8y |
Так как в 2010 г. количество детей относилось к количеству взрослых как 2:3, получим уравнение: \(\displaystyle \frac{x}{y}=\frac{2}{3},\) или 3x = 2y.
В 2020 г. это отношение стало равно 5:8, отсюда второе уравнение: \(\displaystyle \frac{x+55}{1,8y}=\frac{5}{8}\);
\( 8(x + 55) = 5 \cdot 1,8y.\)
Мы получили систему двух уравнений с двумя неизвестными:
\(\left\{ \begin{array}{c}
3x=2y \\
8\left(x+55\right)=5\ \cdot 1,8y \end{array}
\right. ;\)
\(\left\{ \begin{array}{c}
y=\ \frac{3x}{2} \\
8(x+55)=9y \end{array}
\right. ; \)
\(\left\{ \begin{array}{c}
y=\ \frac{3x}{2} \\
8(x+55)=9\cdot \frac{3x}{2} \end{array}
\right. . \)
Решим отдельно второе уравнение системы: \(8(x+55)=9\cdot \frac{3x}{2}\)
Из второго уравнения системы: x = 80.
Тогда \(y=\ 120.\)
Значит, в 2010 году было детей — 80 тысяч, а взрослых — 120 тысяч. Всего население города составляло 80 + 120 = 200 тысяч человек.
Ответ: 200000
10. На рисунке изображён график функции вида \(\displaystyle f\left(x\right)=\frac{ax+b}{x+c},\ \) где числа a, b и c — целые. Найдите b.
Решение:
Преобразуем формулу функции, выделив целую часть.
\(\displaystyle f\left(x\right)=\frac{ax+b}{x+c}=\frac{ax+ac+b-ac}{x+c}=\frac{ax+ac}{x+c}+\frac{b-ac}{x+c}=\)
\(\displaystyle =a+\frac{b-ac}{x+c}.\)
График функции имеет горизонтальную асимптоту \(y=4,\) значит, \(a=4.\)
График функции имеет вертикальную асимптоту \(x=-2,\ \) значит, \(c=2.\)
График функции проходит через точку с координатами (-5; 3), значит, \(f\left(-5\right)=3.\ \)
\(\displaystyle 4+\frac{b-4 \cdot 2}{-5+2}=3; b=11.\)
Ответ: 11
11. Найдите наименьшее значение функции \(y=e^{2x}-4e^x+6\ \) на отрезке \([0;3].\)
Решение:
Найдём производную функции: \(y'=2e^{2x}-4e^{x}=2e^{x}(e^{x}-2).\)
Приравняв производную к нулю, получим: \(2e^{x} (e^{x}-2)=0.\)
Так как \(e^{x}\ne 0,\) то \(e^{x}-2=0, \ e^{x}=2, \ x= ln 2. \) Найдём, где на оси X расположена эта точка.
Сравним \(ln 2\) и 0. Так как \(0=ln 1\) и \(2 \textgreater 1,\) получаем, что \( ln 2 \textgreater 0.\)
Также \(ln 2 \textless 1,\) поскольку \(1 = ln e\) и \(e \textgreater 2\)

Мы получили, что 0 \(\textless ln\ 2\textless 1,\) то есть точка экстремума принадлежит отрезку [0; 3]. Определим знаки производной левее и правее точки экстремума:
\(y'\left(0\right)=\ 2e^0(e^0-2) = 2 \cdot \left(-1\right)=-2\textless 0\)
\(y'\left(1\right)=\ 2e^1(e^1-2)\) =2е(е — 2) \(\textgreater 0.\)
При переходе через точку x = ln 2 производная меняет знак с минуса на плюс, следовательно в этой точке минимум функции. Поэтому \(y_{min}=y\)(ln 2).
Если x = ln 2 , то \(e^x=2\) и \(e^{2x}=({e^x)}^2=2^2=4.\) Получим \(y_{min}=y\)(ln 2) = 4 — 4 \(\cdot 2+6=2.\)
Ответ: 2
Часть 2. Задания с развернутым ответом.
12. а) Решите уравнение:
\(\displaystyle \frac{1}{{sin}^2\pi x} - \frac{3}{{cos\ (\frac{11{\pi }^{\ }}{2}\ +\ \pi x)\ }\ }=-2\)
б) Укажите корни этого уравнения, принадлежащие отрезку [-2; -0,5].
Решение:
а) Применим формулу приведения:
\(\displaystyle {cos \left(\frac{11\pi }{2}+ \pi x\right)={cos \left(4\pi +\frac{3\pi }{2}+ \pi x\right)={cos \left(\frac{3\pi }{2}+ \pi x\right)={sin \pi x}.\ }\ }\ }\), получим уравнение: \(\displaystyle \frac{1}{sin^2 \pi x}-\frac{3}{sin \pi x}=-2.\)
Пусть \(\displaystyle t=\frac{1}{{sin \pi x\ \ }},\) тогда

Вернёмся к исходной переменной:
\( \left[ \begin{array}{c}
\displaystyle \frac{1}{sin\ \pi x}=1 \\
\displaystyle \frac{1}{sin\ \pi x}=2 \end{array}
\right. \Leftrightarrow \ \left[ \begin{array}{c}
{sin \pi \ }x=\displaystyle \frac{1}{2} \\
{sin \pi \ }x=1 \end{array}
\right. \Leftrightarrow \left[ \begin{array}{c}
\pi x=\displaystyle \frac{ \pi }{6}+2 \pi k,\ \\
\pi x=\displaystyle \frac{5 \pi }{6}+2 \pi k \\
\pi x=\displaystyle \frac{ \pi }{2}+2 \pi k,\ \ \ k\in Z \end{array}
\right. \Leftrightarrow
\newline
\Leftrightarrow \left[ \begin{array}{c}
x=\displaystyle \frac{1}{6}+2k,\ \\
x=\displaystyle \frac{5}{6}+2k \\
x=\displaystyle \frac{1}{2}+2k,\ \ \ k\in Z \end{array}
\right.\)
б) Отметим на числовой прямой отрезок [-2; - 0,5] и найденные серии решений.
1) Если \(\displaystyle x=\frac{1}{6}+2k,\) k\(\in Z,\) то
при k = - 1 получим
x = \(\displaystyle \frac{1}{6}+2\ \cdot \left(-1\right)=\frac{1}{6}-2=-1\frac{5}{6}=-\frac{11}{6};\)
2) Если \(\displaystyle x=\frac{5}{6}+2k,\) k\(\in Z,\) то при k = - 1 получим \(\displaystyle x=\frac{5}{6}+2\ \cdot \left(-1\right)=\frac{5}{6}-2=-1\frac{1}{6}=-\frac{7}{6}\) ;
3) Если \(\displaystyle x=\frac{1}{2}+2k,\) \(k\in Z,\) то при k = - 1 получим \(\displaystyle x=\frac{1}{2}+2\ \cdot \left(-1\right)=\frac{1}{2}-2=-1\frac{1}{2}=-1,5.\)
Для всех трех серий решений при k \(\le -2\ \) или \(k\ \ge 0\) корни уравнения не лежат на отрезке [-2; - 0,5].
Ответ:
а) \(\displaystyle \frac{1}{6} + 2k;\) \(\displaystyle \frac{5}{6} + 2k;\) \(\frac{1}{2} + 2k\) k — целое.
б) \(\displaystyle -\frac{11}{6};\) \(-1,5;\) \(\displaystyle -\frac{7}{6}\)
13. В основании правильной треугольной призмы \({ABCA}_{1}{B}_{1}{C}_{1}\) лежит треугольник ABC. На прямой \({AA}_{1}\) отмечена точка D так, что \({A}_{1}\) — середина AD. На прямой \({B}_{1}{C}_{1}\) отмечена точка E так, что \({C}_{1}\) — середина \({B}_{1}E\).
а) Докажите, что прямые \({A}_{1}{B}_{1}\) и DE перпендикулярны.
б) Найдите расстояние между прямыми AB и DE, если AB = 4, а \({AA}_{1}=1.\)
Решение:
а) Продлим отрезки ВА и ВС, увеличив их вдвое. Достроим еще один «этаж» призмы. Теперь наша призма стала частью большой призмы.
\(\left. \begin{array}{c}
AD\bot A_1B_1 \\
A_1E\bot A_1B_1 \end{array}
\right\}\Rightarrow \left(A_1DE\right)\bot \left(A_1B_1\right).\)
Мы применили признак перпендикулярности прямой и плоскости.
Значит, \(DE\bot A_1B_1,\ \)поскольку прямая \(DE\ \)лежит в плоскости \(\left(A_1DE\right).\)
б) Найдем расстояние между прямыми AB и DE. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.
\(DE\in AFK,\ \left(AFK\right)\bot AB.\)
В плоскости AFK проведём \(AT\bot DE.\) Это и будет общий перпендикуляр.
Найдем АF из прямоугольного треугольника АВF, \(AF=\sqrt{64-16}=4\sqrt{3}.\)
Из прямоугольного треугольника \(AA_1E:AE=\sqrt{48+1}=7.\)
Рассмотрим \(\vartriangle ADE; \ \) он равнобедренный, \(AE=DE=7, \) AT — его высота.
Запишем площадь треугольника АDE двумя способами.
\(\displaystyle S_{ \vartriangle ADE}=\frac{1}{2}\ AD\cdot A_1E=\frac{1}{2}DE\cdot AT.\ \) Отсюда
\(7AT=8\sqrt{3},\)
\(\displaystyle AT=\frac{8\sqrt{3}}{7}.\)
Ответ: \(\displaystyle \frac{8 \sqrt{3}}{7}\)
14. Анна Малкова
Решите неравенство: \(\sqrt{{{log}_5 x\ }}\) + \(2\sqrt{{{log}_x 5\ }}\geq 3\)
Решение:
\(\sqrt{{{log}_5 x\ }}\) + \(2\sqrt{{{log}_x 5\ }}\geq 3\)
Замена: \(\sqrt{{log}_5x}=t,\ \ t\textgreater 0,\) тогда \(\displaystyle \sqrt{{log}_x5}=\frac{1}{t}\)
\(\displaystyle t+\frac{2}{t}\ge 3\)
\(\left(t-1\right)(t-2)\ge 0, \)

Вернемся к переменной х
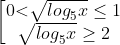
Функция \({log}_5x\) монотонно возрастает, поэтому если \({log}_5x_1\textgreater \ {log}_5x_2,\) то \(x_1\textgreater x_2\)
при \(x_1 \textgreater 0,\) \(x_2\textgreater 0.\)
Получим:
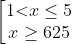
Ответ: \(\left(1;5]\cup [625;\ +\infty \right )\)
15. Александра Антонова
В июле планируется взять кредит в банке на сумму 16 млн рублей на n лет.
Условия его возврата таковы:
- каждый январь долг возрастает на 5% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
На сколько рублей пятый платеж отличается от восьмого платежа, если известно, что общая сумма выплат после полного погашения кредита равна 20,4 млн рублей?
Решение:
По условию, кредит погашается по схеме с дифференцированными платежами, уменьшение суммы долга — равномерное.
Переплата по кредиту равна 20,4 — 16 = 4,4 млн рублей.
Найдем, за сколько лет будет выплачен кредит. Применим формулу для величины переплаты.
\(\displaystyle \prod =\frac{n+1}{2}\cdot \frac{r}{100}\cdot S\)
Здесь r — процент банка, S — сумма кредита, n — количество месяцев.
\(\displaystyle \prod =\frac{n+1}{2}\cdot \frac{5}{100}\cdot 16=4,4\)
\(\displaystyle \frac{n+1}{2}\cdot \frac{5\cdot 4}{100}=1,1\)
\(n=10,\) кредит взяли на 10 лет.
Пусть \(\displaystyle k=1+ \frac{r}{100}\) — коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов. Составим схему погашения кредита. В первой строке — сумма долга после очередной выплаты, во второй — сумма долга после начисления процентов, \(z_1,\ z_2\dots \ z_{10}-\ \) выплаты.
\(\displaystyle z_1=Sk-\frac{9}{10}S;\)
\(\displaystyle z_2=\frac{9}{10}Sk-\frac{8}{10}S; \ \)
\(\displaystyle z_3=\frac{8}{10}Sk-\frac{7}{10}S;\)
\(\displaystyle z_5=\frac{6}{10}Sk-\frac{5}{10}S;\)
\( \dots \)
\(\displaystyle z_8=\frac{3}{10}Sk-\frac{2}{10}S.\)
Найдем разницу между пятой и восьмой выплатами:
\(\displaystyle Z_5-Z_8=\frac{3}{10}Sk-\frac{3}{10}S=0,3\cdot S\cdot \frac{5}{100}=\frac{0,3\cdot 16\cdot 5}{100}=\frac{24}{100}=240\) тысяч рублей.
Ответ: 240 000 рублей.
16. Антон Акимов
В трапеции ABCD точки M и N — середины боковых сторон AB и CD соответственно. Известно, что AD = 14, CM = 5, AN = 5, а высота трапеции равна 8.
а) Докажите, что около трапеции ABCD нельзя описать окружность.
б) Известно, что АD \(\textgreater \) BC. Найдите площадь трапеции ABCD.
Решение:
а) CM = AN. Докажем, что около трапеции ABCD нельзя описать окружность.
СМ — медиана \(\triangle ABC,\) АN - медиана \(\triangle \) ACD.
«Удвоим» отрезки CM и AN и получим точки К и L на продолжениях оснований трапеции AD и BC за точки A и C соответственно. Тогда \( CM\cap AD=K,\) \(BC \cap AN=L.\)
\(\triangle BMC=\triangle AMK\) ( по стороне и двум прилежащим углам), тогда ВС = АК и СМ = КМ.
Аналогично, AD = CL и AN = LN из равенства \(\triangle LNC=\triangle AND.\ \ \ \)
Предположим, что около трапеции ABCD окружность описать можно. Тогда эта трапеция является равнобедренной. МN — средняя линия трапеции, и трапеция AMND также является равнобедренной. Диагонали равнобедренной трапеции равны: AN = MD. Тогда получаем, что AN = MD = CM.
Таким образом, треугольник CMD равнобедренный: CM = MD = 5. Его медиана MN должна быть также его высотой. Но это означает, что боковая сторона CD равнобедренной трапеции перпендикулярна её средней линии (и основаниям), чего быть не может. Полученное противоречие доказывает, что около трапеции ABCD нельзя описать окружность.
б) Поскольку треугольники ВМС и АMК, а также треугольники \(LNC\) и \(AND\) равны, мы можем вместо площади искомой трапеции ABCD вычислять площадь равнобедренной трапеции LCKA:
Высота у них общая h = 8.
Из пункта (а) имеем: BC = AK и CL = AD, тогда \(S_{ABCD}=S_{LCKA}.\)
Трапеция LCKA — равнобедренная. В ней известны боковые стороны, LA = CK = 10, высота h = 8, а также одно из оснований LC = 14.
Проведем две высоты \(KF\bot CL,\ \ \ AT\bot CL,\) тогда \(KF=AT=h=8.\)
\(\ \triangle KFC=\triangle ATL\) ( по катету и гипотенузе), по теореме Пифагора
\(CF = LT = \sqrt{{KC}^2-{KF}^2}=\sqrt{{10}^2-8^2}=6.\)
LC — большее основание трапеции LCKA, АК — меньшее основание.
AK = 14 — 12 = 2. Площадь трапеции равна
\(\displaystyle S_{ABCD}=S_{LCKA}=\frac{AK+CL}{2}\cdot AT=\frac{2+14}{2}\cdot 8=64.\)
Ответ. 64
17. Анна Малкова
При каких значениях параметра а уравнение \({sin (\pi (\sqrt{a-x^2}-x)\ })=0\)
имеет ровно 2 решения?
Решение:
Сделаем замену:
\(\pi \left(\sqrt{a-x^2}-x\right)=t,\) получим уравнение sin t = 0. Отсюда \(t =\pi k,\) \(k\in Z.\)
Вернемся к переменной x:
\(\pi \left(\sqrt{a-x^2}-x\right)=\pi k, \ \ \ k\in Z.\)
\(\sqrt{a-x^2}=x+k,\ \ \ k\in Z\)
ОДЗ: \(a-x^2\ge 0\)
1) если \(a\textless 0\ ,\) то \(a-x^2\textless 0\) — не выполняется условие ОДЗ.
2) если \(a=0,\) то \(\sqrt{-x^2}=x+k,\ \ \ k\in Z\)
Уравнение имеет единственное решение при \(k=0\) и \( x=0.\) Это не подходит по условию задачи.
3) Рассмотрим случай \(a\textgreater 0.\) Пусть \(a=R^2.\)
Решим графически уравнение \(\sqrt{R^2-x^2}=x+k,\) \(k\in Z\)
Построим графики левой и правой частей этого уравнения.
График левой части уравнения \(y=\sqrt{R^2-x^2}\) — верхняя полуокружность с центром в начале координат и радиусом \(R \textgreater 0.\)
График правой части \(y=x+k,\) где \(k\in Z\ \ \ \ \ \) — семейство прямых с угловым коэффициентом 1.
Чем больше радиус, тем больше параллельных прямых пересекает полуокружность.
Уравнение имеет ровно два решения только в случае, когда полуокружность пересекает прямую
y = x и касается прямой y = x + 1 в точке А.
Рассмотрим прямоугольный треугольник ОВС — равнобедренный, так как ОС = ОВ = 1.
\(\angle OCB=\angle OBC=45{}^\circ ,\) тогда ОА — медиана и высота, ОА = R = \(\frac{\sqrt{2}}{2}.\)
\(a=R^2={\left(\frac{\sqrt{2}}{2}\right)}^2=\frac{1}{2} .\)
Если радиус окружности меньше\(\ \ \frac{\sqrt{2}}{2}\ ,\) то уравнение имеет единственное решение.
Если радиус окружности больше \(\frac{\sqrt{2}}{2}\) , то уравнение имеет 3 и более решений.
Уравнение имеет ровно 2 решения при \(a=\)\(\frac{1}{2}\) .
Ответ: \(\ 0,5\)
18. а) Существуют ли натуральные числа m и n, такие, что дискриминант квадратного трехчлена \(x^2+mx+n\) равен 17?
б) Существуют ли натуральные числа m и n, такие, что дискриминант квадратного трехчлена \(x^2+mx+n\) равен 54?
в) Какое наименьшее значение принимает дискриминант D квадратного трехчлена \(x^2+\left(3m+n\right)x+\left(3n+m\right),\ \)если известно, что числа m, n и D — натуральные?
Решение:
а) Да, существуют.
Предположим, что \(D = m^2-4n,\) тогда \(m^2-4n=17;\) \(m^2=4n+17.\)
Так как \(4n\) — четно, то \(4n+17\) — нечетное число, следовательно \(m^2-\) также нечетное \(m^2\textgreater 17.\)
Пусть m = 5, тогда n = 2. Получим, что \(25 = 4\cdot 2+17\) — верное равенство.
Да, существуют.
m = 5, n = 2 и D = 17.
б) Нет, такого быть не может.
Предположим, что для квадратного трехчлена \(x^2+mx+n\) дискриминант \(D=54.\ \)
Тогда \(m^2-4n\) = 54;
\(m^2=4n+54\)
Правая часть равенства \(4n+54\) — четна, значит и левая часть равенства тоже четна, то есть \(m^2\) — четно. Следовательно, m — четное число.
Если m — четное число, то \(m^2\) делится на 4. Тогда в равенстве \(m^2-4n = 54\) левая часть делится на 4, а правая часть 54 — не делится на 4.
Получили противоречие, значит, предположение неверно и \(D=54\) — не может быть.
в) Дан квадратный трехчлен \(x^2+\left(3m+n\ \right)x+(3n+m).\)
Нужно найти \(D_{min}\) , где \(m, n, D\in N.\)
\(D={\left(3m+n\right)}^2-4\left(3n+m\right)={\left(3m+n\right)}^2-12n-4m=\)
\(={\left(3m+n\right)}^2-12\left(3m+n\right)+32m=\)
\(={\left(3m+n\right)}^2-12\left(3m+n\right)+36-36+32m={\left(3m+n-6\right)}^2+32m-36\)
Получили: \(D = {(3m+n-6)}^2+ 32m - 36. \)
Чем больше m, тем больше D (при фиксированном n).
Так как \(m \in N,\) то \(m\ge 1.\) Возьмем \(m=1,\ \)тогда D = \({(n-3)}^2-4.\)
Рассмотрим функцию \(f(x) = {(x-3)}^2-4\) и найдем \(f_{min}(x)\) при условии, что \(x\in N, \\) \( \ f(x) \in N.\)
Изобразим схематично график функции \(f(x) ={(x-3)}^2-4.\)
Получим, что если \(1\le x\le 5,\) то \(f(x)\le 0\) — не подходит;
Если \(-\infty \textless x\textless 1,\) то x — не является натуральным числом, не подходит,
Значит, x \(\textgreater 5,\) следовательно \(x\ \ge 6,\) а на отрезке \([6; +\infty )\) функция f(x) монотонно возрастает, следовательно, \(f_{min}(x)= f(6) = 5. \)
Получили, что при n = 6 и m = 1 достигается наименьшее значение D, \(D_{min} = 5.\)
Если \(m\ge 2,\) тогда \( D\ \ge n^2+64-36;\) \(D\ \ge n^2+28\ \textgreater 5.\)
Значит, \(D_{min}=5\) при n = 6, m = 1.
Ответ: а) да; б) нет; в) 5