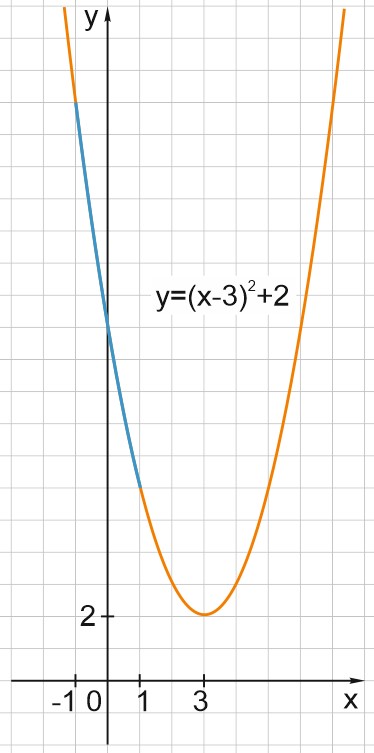ЕГЭ-2023 Вариант 1, решения

Видеоразбор: https://www.youtube.com/watch?v=z9Ou_z7x8C0&t\&t=4552s
и https://www.youtube.com/watch?v=vdzNSD07n1A&t\&t=8s

Часть 1. Задания с кратким ответом

1. В прямоугольном треугольнике гипотенуза равна 10, а один из острых углов равен 15 градусов. Найти высоту, проведенную из вершины прямого угла.

Pешение:

Пусть угол $B$ равен 15 градусам.
Из прямоугольного треугольника $ABC$ : $b=c \sin B,$
Из прямоугольного треугольника $ACH$ : $h=b \cos B.$ . Получим:
$h=c \sin B cos B=10 \sin15^{\circ}cos15^{\circ}=5\sin30^{\circ}=2,5$

Oтвет: 2,5

2. Анна Малкова

У Валентины Петровны есть два ведра для поливки огорода: одно цилиндрическое, другое в форме конуса. Радиус окружности конуса и радиус цилиндрического ведра одинаковы, а еще у цилиндрического ведра высота в 2 раза больше, чем у ведра в форме конуса. Во сколько раз больше воды помещается в цилиндрическое ведро?

Pешение:

Пусть $h_{1}$ - высота цилиндра, тогда высота конуса $h_2=\frac{h_1}{2}$
Объем цилиндра ;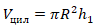
Объем конуса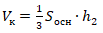

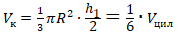
В цилиндрическое ведро помещается в 6 раз больше воды.

Oтвет: 6

3. Анна Mалкова

В морской экскурсии участвуют 16 туристов, в том числе Андрей и Наташа. В каждой лодке 4 места для туристов, места в лодках распределяются случайным образом. С какой вероятностью Андрей и Наташа окажутся в одной лодке?

Pешение:

По условию, всего 4 лодки и в каждой по 4 места.
Пусть в одной из лодок заняла место Наташа. В этой лодке осталось еще 3 места, а всего мест для Андрея осталось 15 (16-е занято Наташей). Получаем 3 благоприятных места из 15 возможных для Андрея.
Поэтому $p=\frac{3}{15}=\frac{1}{5}=0,2$ .

Oтвет: 0,2

4. Анна Mалкова

С какой вероятностью в случайно выбранном месяце високосного года будет 5 воскресений? Ответ округлите до сотых.

Pешение:

В году 12 месяцев. Из них 7 месяцев – такие, что в них 31 день.
4 месяца по 30 дней, и если год високосный, то в феврале 29 дней.
Каждые 28 дней, идущих подряд, – это 4 недели, и в каждых 28 идущих подряд днях ровно 4 воскресенья.
Если в месяце 31 день, то в 28 днях будет 4 воскресенья. Остается 3 дня. Вероятность того, что один из них воскресенье, равна $\frac{3}{7}$ .
Если в месяце 30 дней, то в 28 днях будет 4 воскресенья. Остается 2 дня. Вероятность того, что один из этих дней воскресенье, равна $\frac{2}{7}$ .
Если в месяце 29 дней (это високосный февраль), то это 4 недели и еще один день. Вероятность того, что этот день воскресенье, равна $\frac{1}{7}$ .
Получим: $\frac{7}{12}\cdot\frac{3}{7}+\frac{4}{12}\cdot \frac{2}{7}+\frac{1}{12}\cdot \frac{1}{7}=\frac{30}{84}=\frac{5}{14} \approx 0,36$ .

Oтвет: 0,36

5. Анна Mалкова

Решите уравнение: $\sqrt[]{24-5x}=-x$ .

Если уравнение имеет несколько корней, в ответе запишите больший корень.

Pешение:

Арифметический квадратный корень из числа $a$ - это такое число, что:
$\sqrt{a}\geqslant 0$ и $(\sqrt[]{a})^2=a$ .
Наше уравнение равносильно системе.
$\sqrt{24-5x}=-x$ ⇔ $\left\{\begin{matrix}-x\geqslant 0 \\24-5x\geqslant 0\\24-5x=x^2\end{matrix}\right.$ ⇔ $\left\{\begin{matrix}x^2+5x-24=0\\x\leqslant 0\end{matrix}\right.$ ⇔
⇔ $\left\{\begin{matrix}\left[\begin{array}{ccc}x=3\\x=-8 \\\end{array}\right. \\x\leqslant 0\end{matrix}\right.$ ⇔ $x=-8$

Oтвет: - 8

6. Внесите под корень и вычислите: $(\sqrt{3}-2)\sqrt[]{7+4\sqrt{3}}$ .

Pешение:

Заметим, что $\sqrt{3}$ < $2$ . Результат получится отрицательный.

$(\sqrt{3}-2)\sqrt{7+4\sqrt{3}}=-(2-\sqrt{3})\sqrt{7+4\sqrt{3}}=$

$= -\sqrt{(2-\sqrt{3})^2(7+4\sqrt{3})}=-\sqrt{(4-4\sqrt{3}+3)(7+4\sqrt{3})}=$

$= -\sqrt{(7-4 \sqrt{3})(7+4 \sqrt{3})}=-\sqrt{7^2-(4\sqrt{3})^2}=-\sqrt{49-48}=$

$=-1$

Oтвет: -1

7. На рисунке изображен график функции f(x), определенной на отрезке
[-4,5; 3,5]. Найдите количество точек максимума функции f(x) на данном отрезке.

Pешение:

Что такое точка максимума?
Точка максимума – это такая внутренняя точка области определения функции, в которой значения функции больше, чем во всех достаточно близких к ней соседних точках («горка» на графике функции).
На отрезке [-4,5; 3,5] три такие точки.

Oтвет: 3

8. После дождя уровень воды в колодце может повыситься. Коля бросает небольшие камешки в колодец, измеряя время их падения, и рассчитывает расстояние до воды по формуле $h=5t^2$ , где $h$ — расстояние в метрах, $t$ — время падения в секундах. До дождя камушки падали 1,6 с.
На сколько поднялся уровень воды после дождя, если измеряемое время уменьшилось на 0,2 с? Ответ выразите в метрах.

Решение:

После дождя уровень воды в колодце станет выше, а расстояние до воды уменьшится. Значит, и время падения камешка уменьшится, став равным 1,4 с.
Пусть $h_1=5\cdot 1,6^2$ — расстояние до воды до дождя, $h_2=5\cdot 1,4^2$ — расстояние до воды после дождя.
Уровень воды поднимется на $h_1-h_2=5\cdot 1,6^2-5 \cdot 1,4^2=5(1,6-1,4)(1,6+1,4)=3$ метра.

Oтвет: 3

9. Исаак Ньютон

Трава на всем лугу растет одинаково густо и быстро. Известно, что 70 коров поели бы ее за 24 дня, а 30 коров – за 60 дней. Сколько коров поели бы всю траву за 96 дней? Предполагается, что коровы поедают траву равномерно.

Pешение:

Пусть M кг – масса травы, которая уже есть на лугу. Так как трава растет одинаково густо и быстро, то за каждый день вырастает одинаковое количество травы.

Обозначим за $x$ кг/день – скорость роста травы. Каждый день масса травы на лугу увеличивается на $x$ килограмм.
Пусть одна корова съедает в день $y$ кг травы. Тогда 70 коров съедят за день $70\cdot y$ кг травы.

Представим, что 70 коров пришли на луг, на котором уже есть трава (и ее $M$ килограмм по всему лугу). Коровы едят траву, но при этом трава продолжает расти со скоростью $x$ кг в день. Запишем условие: 70 коров поели бы всю траву за 24 дня:

$M+24x=24 \cdot 70 \cdot y$

Слева в уравнении – количество выросшей на лугу травы. Справа – количество травы, скушанной коровами, и они равны друг другу.
Пусть $n$ – количество коров, которые поели бы всю траву за 96 дней.

$\left\{\begin{matrix}M+24x=24\cdot 70 \cdot y \\M+60x=60 \cdot 30 \cdot y\\M+96x=96 \cdot n \cdot y \end{matrix}\right.$ ⟺ $\left\{\begin{matrix}M+24x=1680 \cdot y\\M+60x=1800 \cdot y\\M+96x=96n \cdot y \end{matrix}\right.$

Складываем три уравнения системы: $3M+180x=(3480+96n)\cdot y$
Разделим обе части уравнения на 3: $M+60x=1160\cdot y +32ny$

Используя полученное уравнение и второе уравнение системы, получим:
$1160\cdot y+32ny=1800\cdot y$
$32n=640$
$n=20$

Oтвет: 20

10. Анна Mалкова

На рисунке изображены графики функций $f(x)=ax^2+bx+c$ и $g(x)=kx+d$ пересекаются в точках A и B. Найдите ординату точки B.

Pешение:

1) Начнем с функции $g(x)$ .

$g(x) = kx + d$

Если $x=0$ , то $g(x)=d$ , тогда $d=-3$ (ордината точки А, где $g(x)$ пересекает ось ординат).

$k$ - это тангенс угла между прямой $y=kx+d$ и положительным направлением оси ОХ.

Берем выделенные (жирные) точки, достраиваем до прямоугольного треугольника и находим тангенс угла.

$k=tg\alpha =\frac{16}{4}=4$

$g(x)= 4x-3$

2) $f(x)=ax^2+bx+c$

График функции $f(x)$ получен из графика $y_1=x^2$ сдвинутым на $m$ единиц по горизонтали и на $n$ по вертикали растяжением в $a$ раз вдоль оси ОУ.

Получили: $f(x)=p(x-m)^2+n$

В нашем случае: $m=1$ ; $n=-5$ .

$f(x)=a(x-1)^2-5$ . Подставив $f(0)=-3$ , найдем $a=2$ .

3) Найдём точки пересечения прямой и параболы.
Получим уравнение:

$2(x-1)^2-5=4x-3$

$2x^2-4x-3=4x-3$

$2x^2-8x=0$

$\left[\begin{array}{ccc}x=0\\x=4 \\\end{array}\right. \\$

$x=0$ - это абcцисса точки $A$

$x=4$ - это абcцисса точки $B$

Ответ: 4

11. Анна Малкова

Найдите наименьшее значение функции $y=x^2-6x+11$ на отрезке $[-1;1].$

Pешение:

$y=x^2-6x+11=x^2-6x+9+2=(x-3)^2+2$ ,

график этой функции получен из графика функции $y=x^2$ сдвигом на три единицы вправо и на две единицы вверх.

Данная функция на отрезке [-1; 1] монотонно убывает и поэтому наименьшее значение функции достигается в правом конце отрезка.

$y_{min}=y(1)=6$

Oтвет: 6

Часть 2. Задания с развернyтым ответом

12.

а) Решите уравнение $2cos^2x+5sinx=5$

б) Найдите все корни уравнения на отрезке $[-\frac{\pi}{2};2\pi]$

Pешение:

$2cos^2x+5sinx=5$

а) Согласно основному тригонометрическому тождеству, $\cos^2x+sin^2x=1$ . Выразим $\cos^2x$ .

$2(1-\sin^2 x)+5\sin x=5$

$2-2 \sin^2 x+5 \sin x - 5 = 0$

$-2\sin^2x+5\sin x-3=0$

$2 \sin^2 x-5\sin x +3=0$

Сделаем замену $\sin x=t$ , $|t|\leq 1$

$2t^2-5t+3=0$

$D=(-5)^2-4\cdot 2\cdot 3=25-24=1$ , $\sqrt{D}=1$

$\left[\begin{array}{ccc}t_1=1\\t_2=\frac{3}{2} \\\end{array}\right. \\$ ; так как $|t|\leq 1$ , подходит только корень $t_1=1$ .

Тогда $\sin x=1$ ⟺ $x=\frac{\pi}{2}+2\pi n$ , $n\in Z$

б) Найдем корни уравнения на отрезке $[-\frac{\pi}{2};2\pi]$ с помощью двойного неравенства.

$-\frac{\pi}{2} \leq \frac{\pi}{2} + 2\pi n\leq 2\pi$

Разделим обе части неравенства на $\pi$ .

$-\frac{1}{2} \leq \frac{1}{2}+2n\leq2$

Вычтем $\frac{1}{2}$ из обеих частей неравенства.

$-1 \leq 2n\leq 1,5$

Разделим на 2 обе части неравенства:

$-0,5 \leq n\leq 0,75$

Единственное целое решение – это $n=0$ . Тогда $x=\frac{\pi}{2}$ – это единственный корень, который принадлежит отрезку $[-\frac{\pi}{2};2\pi]$ .

Oтвет: $\frac{\pi}{2}$

13. Анна Малкова

В основании четырехугольной пирамиды SABCD лежит прямоугольник $ABCD$ , в котором $AB = 4$ , $BD = 4\sqrt{2}$ . Известно, что $SB = \sqrt{11}$ , $SA = SC = 3\sqrt{3}$ .

а) Докажите, что ребро $SD$ перпендикулярно прямой $AC$ .

б) Найдите диаметр шара, описанного вокруг пирамиды $SABCD$ .

Pешение:

а) Так как по условию $AB=4$ , $BD=4\sqrt{2}$ , то прямоугольник $ABCD$ – квадрат.
Рассмотрим $\triangle ASB$ :
$SA=3\sqrt{3}=\sqrt{27}$ (по условию)
$AB=4$ , $SB=\sqrt{11}$ (по условию), тогда $SA^2=AB^2+SB^2$ .
Для треугольника $\triangle ASB$ выполняется теорема Пифагора, следовательно, он прямоугольный,
$\angle ABS=90^{\circ}$ .
Аналогично, $\triangle BSC$ – прямоугольный, $\angle CBS=$ 90°.
Значит, $SB\perp AB$ , $SB\perp BC$ => $SB\perp (ABC)$ по признаку перпендикулярности прямой и плоскости.
$SB$ – высота прямоугольной пирамиды $SABCD$ .
Так как $ABCD$ – квадрат, $AC \perp BD$ => $BD$ – проекция $SD$ на плоскость (ABC). По теореме о трех перпендикулярах, $AC\perp SD$ .
б) Найдем диаметр шара, описанного вокруг пирамиды $SABCD$
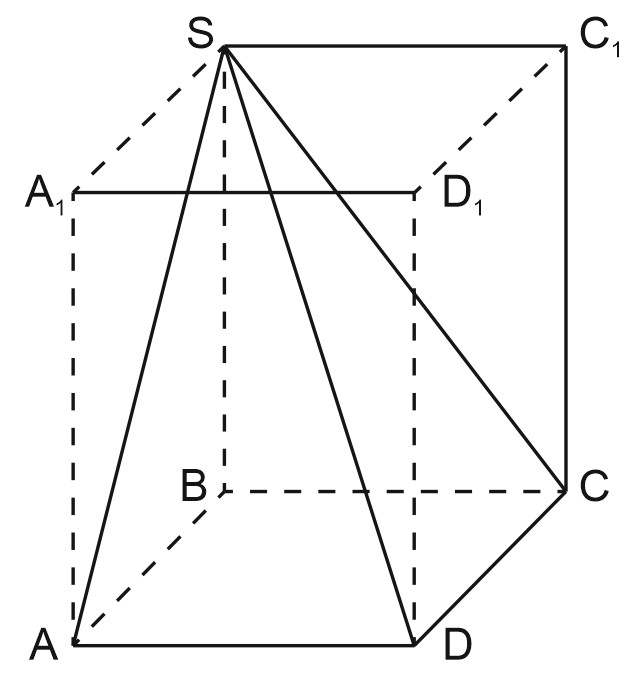
Проведем $AA_1\parallel SB$ , $DD_1\parallel SB$ , $CC_1\parallel SB$ и получим прямоугольный параллелепипед $ABCDA_1SC_1D_1$ .
Пусть $O$ – точка пересечения его диагоналей, $SD \cap AC_1=O$ ,
Точка $O$ равноудалена от всех вершин параллелепипеда, в том числе от $A, B, C, D$ и $S$ , и является центром шара, описанного вокруг пирамиды $SABCD$ .
Диаметр этого шара:
$D=SD=\sqrt{BD^2+SB^2}=\sqrt{32+11}=\sqrt{43}$

Ответ: $\sqrt{43}$

14. Решите неравенство: $\left|x^2-2x\right|$ < $\left|x+4 \right|$ .

Решение:

Так как обе части неравенства неотрицательны, то их можно возвести в квадрат. Получим:
$(x^2-2x)^2$ < $(x+4)^2$
Перенесем все в левую часть и воспользуемся формулой разности квадратов
$(x^2-2x)^2$ &lt< $(x+4)^2$ ⇔ $(x^2-2x)^2-(x+4)^2$ < $0$ ⇔

⇔ $(x^2-2x-x-4)(x^2-2x+x+4)$ < $0$ ⇔

⇔ $(x^2-3x-4)(x^2-x+4)$ < $0$ .

Найдем нули каждого множителя. Для этого решим квадратные уравнения
$x^2-3x-4=0$ и $x^2-x+4=0$ .

1) Корни уравнения $x^2-3x-4=0$ – это $x = - 1$ и $x = 4$ .

$x^2-x+4=0$ - нет решений, $D$ < $0$ . Значит, $x^2-x+4$ > $0$ для всех $x$ .

Получим: $x^2-3x-4$ < $0$ .

$(x+1)(x-4)$ < $0$ . Решив квадратичное неравенство, получим ответ.

Ответ: $(-1;4)$

15. Гражданин положил в банк определенную сумму денег под фиксированный процент годового дохода. За первые два года сумма вклада возросла на 60 тысяч рублей, а за третий год – еще на 49 тысяч рублей. Какой была первоначальная сумма вклада? Ответ выразите в тысячах рублей.

Pешение:

Пусть первоначальная сумма вклада равна S, банк начисляет р процентов годовых, и тогда к концу первого года вклад увеличивается в $k = 1+ \frac{p}{100}$ раза.

К концу второго года вклад увеличится в $k^2$ раз, к концу третьего – в $k^3$ раз.

$S \cdot k^2 = S + 60$ ,

$S \cdot k^3 = S + 109$ .

Мы получили два уравнения и две неизвестных.

Из первого уравнения: $S \cdot (k^2 - 1) = 60$ ,

Из второго: $S \cdot (k^3 - 1) = 109$ .

Разложим по формулам сокращенного умножения $k^2 - 1 = (k-1) \cdot (k+1)$
и $(k^3 - 1) = (k-1) \cdot (k^2 +k+1)$ , а затем поделим второе уравнение на первое:

$\frac{k^2+k+1}{k+1}=\frac{109}{60}$ ;

$\frac{k^2}{k+1}=\frac{49}{60}$ ;

$60k^2-49k-49=0$ ;

$D = 49^2 + 4\cdot 49\cdot 60 = 49 ( 49 + 240) = 49 \cdot 289 =$

$=(7\cdot 17)^2 = 119^2$

$k=\frac{49+119}{120}=\frac{168}{120}=1,4$ ;

$p = 40$ (процентов); $S=\frac{60}{k^2-1 } = \frac{60}{0,96}= 62,5$ .

Ответ: 62,5

16. Анна Малкова

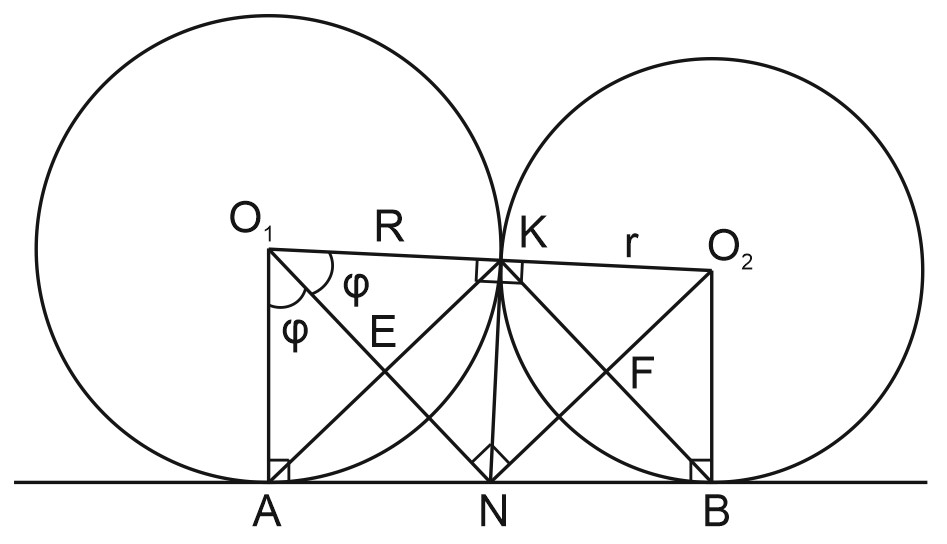
Окружности с центрами $O_{1}$ и $O_{2}$ касаются внешним образом в точке $K$ . Прямая $AB$ касается первой окружности в точке $A$ , а второй — в точке $B$ . На отрезке $AB$ взята точка $N$ так, что $NK$ – общая внутренняя касательная к обеим окружностям.

а) Докажите, что углы $O_1NO_2$ и $AKB$ равны.
б) Пусть $E$ – точка пересечения $AK$ и $O_1N$ , $F$ – точка пересечения $BK$ и $O_2N$ , радиусы окружностей равны 8 и 2. Найдите $EF$ .

Pешение:

а) Докажем, что $\angle O_1NO_2$ =∠ $AKB$ .

Заметим, что $AN=NK=NB$ как отрезки касательных, проведённых из точки $N$ .

Покажем, что $\angle AKB=90$ °.

Точки $A$ , $K$ и $B$ равноудалены от точки $N$ .
Следовательно, они лежат на окружности с центром в точке $N$ , причем $AB$ – диаметр этой окружности. Тогда $\angle AKB=90$ ° как опирающийся на диаметр.

б) Найдём $EF$ .

$\triangle ANK$ – равнобедренный, $NK=NA$ .

Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому $NE$ – биссектриса и высота $\triangle ANK$ , $\angle NEK=90$ °.

Аналогично, $\angle NFK=90$ °, значит, $NEKF$ – прямоугольник. Диагонали прямоугольника равны, поэтому $EF=NK$ .

$EF=NK=\frac{1}{2} AB$ $AB=\sqrt{(R+2)^2-(R-2)^2})=\sqrt{4Rr}=2\sqrt{Rr}$ ;

$EF= NK=\frac{2\sqrt{Rr}}{2}=\sqrt{Rr}= 4$ .

Ответ: 4

17. Анна Малкова

При каком значении параметра $a$ система

$\left\{ \begin{array}{c}2\leq y \leq 2+\sqrt[]{6x-x^2-5} (1) \\\sqrt[]{(x-1)^2+(y-a)^2}+\sqrt[]{(x-5)^2+(y-a)^2}=4 (2) \\\sin \pi x=0 \\\sin \pi y=0 \end{array}\right.$

имеет наибольшее количество решений? Найдите эти решения.

Pешение:

Решим систему графически в системе координат Х; Y. Начнем со второго уравнения системы.

Вспомним, что уравнение отрезка $\begin{bmatrix}AB\end{bmatrix}$ , концы которого – точки $A (x_A; y_A)$ и $B (x_B; y_B)$ имеет вид:

$\sqrt{(x-x_A)^2+(y-y_A)^2}$ + $\sqrt{(x-x_B)^2+(y-y_B)^2)}$ = $\sqrt{(x_B-x_A)^2+(y_B-y_A)^2)}$

В левой части этого длинного уравнения – сумма расстояний от точки $M$ с координатами $(x;y)$ до точек $A (x_A; y_A)$ и $B (x_B; y_B)$ . В правой – расстояние между точками $A$ и $B$ .
с координатами $(x;y)$ до точек $A (x_A; y_A)$ и $B (x_B; y_B)$ . В правой – расстояние между точками $A$ и $B$ .
Пара чисел $(x;y)$ соответствует координатам любой точки этого отрезка.
Кратко это можно записать: $|AM|+|BM|=|AB|$ , и это значит, что точка $M$ лежит на отрезке $\begin{bmatrix}AB\end{bmatrix}$ .

В нашем случае точки $A$ и $B$ имеют координаты: $A(1;a); B(5;a)$ . Расстояние между этими точками равно 4. Первое уравнение задает отрезок $AB$ . Ордината точек $A$ и $B$ равна параметру $a$ . Можно сказать, что это отрезок длины 4, который, в зависимости от параметра $a$ , может быть расположен выше или ниже на координатной плоскости.

Разберемся с неравенством (1).
Уравнение $y=\sqrt{R^2-(x-a)^2}+b$ задает верхнюю полуокружность, центр которой – в точке с координатами $(a;b)$ , а радиус равен $|R|$ .
Значит, неравенство (1) задает область, ограниченную прямой $y=2$ и полуокружностью $\sqrt{(4-(x-3)^2)}+2c$ центром в точке $P(3;2)$ и радиусом равным 2.
Решим уравнения $\sin \pi x=0$ и $\sin \pi y=0$ .
Решения первого уравнения: $x=n$ .
Решения второго уравнения: $y=k$ , где $k$ и $n$ - целые.
Следовательно, уравнения $\sin \pi x=0$ и $\sin \pi y=0$ задают бесконечное множество точек, обе координаты которых – целые числа.
Обратите внимание: переменные $x$ и $y$ независимы, и поэтому мы используем две целые переменные, $n$ и $k$ .

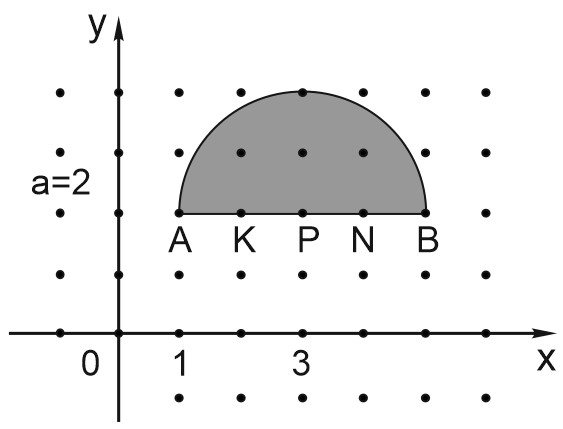
Будем передвигать отрезок, заданный вторым уравнением, вверх-вниз по горизонтали в зависимости от параметра $a$ . Концы этого отрезка – точки $A(1;a); B(5;a)$ . Если $a$ < $2$ , то отрезок не имеет общих точек с областью, заданной первым неравенством. При $a = 2$ он пересекает эту область по ее границе, и система имеет ровно 5 решений, соответствующих точкам $A, K, P, N, B$ . Если $a = 3$ , то решений всего три. При $a = 4$ остается только одно решение, при $a$ > $4$ исходная система не имеет решений. Значит, в случае $a=2$ , система имеет наибольшее число решений, а именно 5.
Ответ: $a=2$ , решения: (1;2); (2;2); (3;2); (4;2); (5;2).

18. В живом уголке четыре ученика кормят кроликов. Каждый кормит нескольких (хотя бы одного) кроликов, но не всех. Первый ученик дает порцию по 100 грамм, второй – по 200 г, третий – по 300 г., а четвертый – по 400 г.
а) Может ли оказаться, что кроликов было 15 и все они получили одинаковое количество корма?
б) Может ли оказаться, что кроликов было 15 и все они получили различное количество корма?
в) Какое наибольшее количество кроликов могло быть в живом уголке, если каждый ученик насыпал корм ровно четырем кроликам и все кролики получили разное количество корма?

Решение:
а) Ответ: да, может. Например, первый и четвертый ученики кормят семь кроликов. Каждый из этих семи кроликов получает по 100 + 400 = 500 г корма. Второй и третий ученики кормят восьмерых оставшихся кроликов, которые также получат по 200 + 300 = 500 г корма.

б) Ответ: нет, не может.
Пусть среди кроликов есть «счастливец», которого покормили все школьники. Он получил максимально возможное количество корма, равное 100 + 200 + 300 + 400 = 1000 г.

Среди кроликов также может быть «невезучий», которого никто не покормил. Он получил 0 грамм корма. Значит, количество корма для одного кролика может принимать 11 значений: 0, 100, 200, 300… 1000 грамм.
Поскольку кроликов 15, а возможных значений только 11, среди этих пятнадцати найдутся кролики, получившие одинаковое количество корма.

в) Если каждый ученик насыпал корм четверым кроликам, то всего ученики раздали кроликам
4∙ (100 + 200 + 300 + 400) = 4000 г. корма.

В пункте (б) мы выяснили, что всего может быть 11 различных значений для количества корма, которое получил кролик. Но если 11 кроликов получают различное количество корма, то общее количество корма равно
0 + 100 + 200 +…+ 1000 = 5500 грамм. Это на 1500 грамм больше, чем 4000 грамм.

Значит, накормить 11 кроликов, соблюдая все условия пункта (в), школьники не смогут.
Вариант с 10 кроликами также невозможен: даже если среди кроликов не будет того, который получил 1000 г, все равно не хватает 500 г корма.

Получается, что число кроликов не больше, чем 9. Мы оценили количество кроликов. Приведем пример, когда кроликов именно 9.

Варианты 1000 г и 500 г отсутствуют. Все условия задачи выполнены – каждый ученик покормил 4 кроликов, и все кролики получили различное количество корма.

Ответ:
а) да
б) нет
в) 9

Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «ЕГЭ-2023 Вариант 1, решения» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 23.09.2023

ЕГЭ-2023 Вариант 1, решения

Это полезно