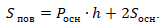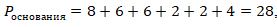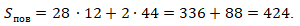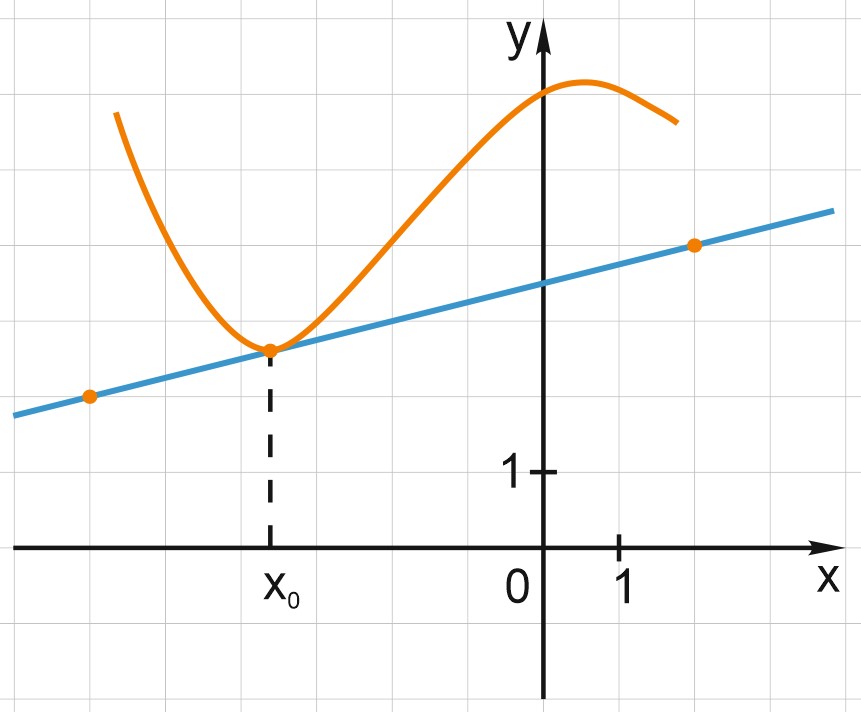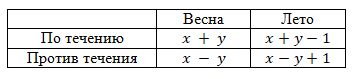Видеоразбор: https://www.youtube.com/watch?v=ZhQ4H_BaR_4&t;t\&t=13s
и https://www.youtube.com/watch?v=w-yTVjQXW4A&t;t\&t=161s
Часть 1. Задания с кратким ответом
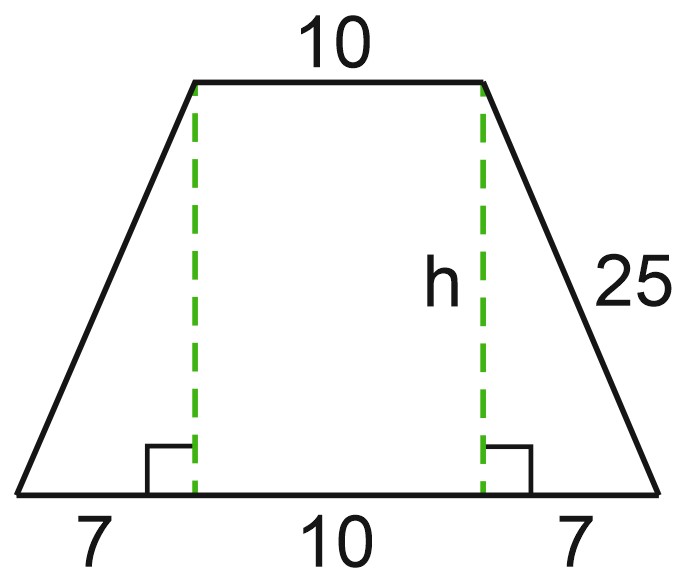
1. В равнобедренной трапеции основания равны 10 и 24, боковая сторона 25. Найдите высоту трапеции.
Pешение:
В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и \(h^2=25^2-7^2=(25-7)(25+7)=18 \cdot 32\). Отсюда \(h=\sqrt{(18\cdot 32)}=\sqrt{(9\cdot 64)}=3\cdot 8=24 \).
Oтвет: 24
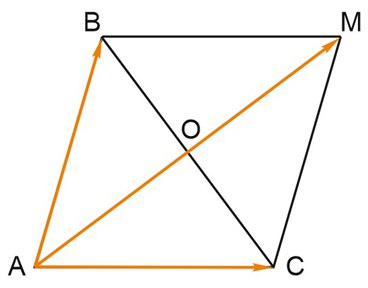
2. Стороны правильного треугольника ABC равны \(2\sqrt{3}\). Найдите длину вектора \( \overrightarrow{AB}+\overrightarrow{AC}\).
Pешение:
Найдем сумму векторов \(\overrightarrow{AB}\) и \(\overrightarrow{AC}\) по правилу параллелограмма.
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}\)
\(\overrightarrow{AM}=2\overrightarrow{AO}\), где O - середина \(BC\).
\(AO\) - медиана, высоты и биссектриса правильного треугольника \(ABC\),
\(AO=AB\cdot\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}\cdot\sqrt{3}}{2}=3\), \(AM=2AO=6\).
Ответ: 6
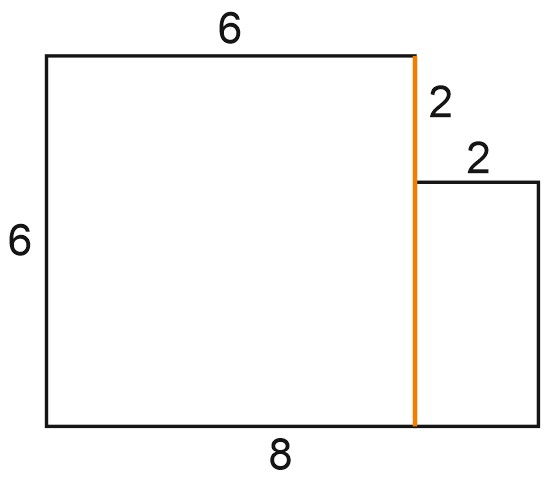
3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Pешение:
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
\(S_{1}=6\cdot 6=36\) (большой квадрат),
\(S_{2}=2\cdot 4=8\) (маленький прямоугольник),
Подставим все данные в формулу 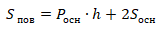
и найдем площадь поверхности многогранника:
Oтвет: 424
4. Александра Антонова
Рэпер Клим готовится выступить на концерте. Он считает, что чем позже выступает артист на концерте, тем он круче. Порядок выступлений определяется случайным образом. С какой вероятностью Клим выступит после своих основных соперников: Гоги и Алекса? Ответ округлите до сотых.
Решение:
Клим может выступить первым, вторым или третьим равновероятно. Вероятность того, что он будет третьим, равна \(\frac{1}{3}\).
Oтвет: 0,33
5. Монету бросают 10 раз. Во сколько раз событие «Орел выпадет ровно 8 раз» более вероятно, чем событие «Орел выпадет ровно 9 раз»?
Pешение:
Начнем с числа возможных исходов. Если мы бросаем монету, возможных исходов два – орел или решка.
Бросим монету два раза (или две монеты одновременно, все равно). И вот уже 4 возможных исхода:
ОО
ОР
РО
РР
(буквой О обозначен выпавший «орел», буквой «р» - решка).
Каждый следующий бросок монеты увеличивает число возможных исходов в 2 раза (орел или решка).
Для 10 бросков монеты количество возможных исходов, очевидно, равно \(2^{10}\).
По определению, вероятность равна отношению числа благоприятных исходов к общему числу исходов.
Рассмотрим случай, когда орел выпадет ровно 9 раз из 10 бросков монеты. Это значит, что решка выпала ровно 1 раз.
Это могло произойти при первом броске, при втором, при третьем… и, наконец, при десятом, всего 10 благоприятных исходов. Вероятность выпадения решки ровно 1 раз из 10 бросков \(P_1=\frac{10}{2^{10}}\).
Теперь случай, когда орел выпал ровно 8 раз из 10 бросков монеты. Значит, решка выпала ровно 2 раза.
Пронумеруем броски: 1,2,3…10.
Решка могла выпасть в первый и во второй раз. Обозначим эту комбинацию 12.
Могла также выпасть в первый и третий раз, в первый и четвертый… Эти комбинации обозначаем как 13, 14…
Пронумеруем таким образом все благоприятные исходы.
12, 13, 14, 15, 16, 17, 18, 19, 1 10
23, 24, 25, 26, 27, 28, 29, 2 10
34, 35, 36, 37, 38, 39, 3 10
45, 46, 47, 48, 49, 4 10
56, 57, 58, 59, 5 10
67, 68, 69, 6 10
78, 79, 7 10
89, 8 10
9 10
Количество благоприятных исходов равно \(9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45\).
Тогда \(P_2=\frac{45}{2^{10}}\).
Поделив \(P_2\) на \(P_1\), получим, во сколько раз выпадение решки ровно 8 раз более вероятно, чем выпадение решки ровно 9 раз:
\(\frac{P_2}{P_1}=\frac{45}{2^{10}}:\frac{10}{2^{10}}=4,5\)
Можно было решить задачу быстрее, с помощью формулы Бернулли.
Пусть проводится \(n\) одинаковых независимых испытаний, в каждом из которых случайное событие А может произойти с вероятностью p или не произойти с вероятностью \(q=1-p\).
Вероятность \(P_n^m\) того, что в \(n\) независимых испытаниях некоторое случайное событие A наступит ровно \(m\) раз, равна:
\(P_n^m=C_n^m p^m q^{n-m}\), где:
\(p\) – вероятность появления события A в каждом испытании;
\(q=1-p\) – вероятность непоявления события A в каждом испытании.
\(C_n^m=\frac{n!}{m!(n-m)!}\)
Найдем вероятность того, что из 10 бросков монеты ровно 9 раз выпадет орел. Это значит, что \(n = 10\), \(m = 9\), \(p=\frac{1}{2}\) (вероятность выпадения орла при одном броске монеты); \( q=\frac{1}{2}\) – вероятность противоположного события (вероятность выпадения решки при одном броске).
\(P_1=P_{10}^9=C_{10}^9\cdot (\frac{1}{2})^9\cdot (\frac{1}{2})^{10-9}\)=\(\frac{10!)}{9!(10-9)!}\cdot \frac{1}{2^{10}}=\frac{10!}{9!\cdot 2^{10}}\) = \(= \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot ... \cdot 1}{9 \cdot 8 \cdot 7 \cdot... \cdot 1 } \cdot \frac{1}{2^{10}}\)\(=\frac{10}{2^{10}}\)
Аналогично, найдем вероятность выпадения 8 орлов при 10 бросках монеты.
\(P_2=P_{10}^8=C_{10}^8\cdot (\frac{1}{2})^8\cdot (\frac{1}{2})^{2}\)=\(\frac{10!)}{8!(10-8)}!\cdot \frac{1}{2^{10}}=\frac{10!}{8!\cdot 2 \cdot 2^{10}}\) = \(= \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot ... \cdot 1}{9 \cdot 8 \cdot 7 \cdot... \cdot 1 } \cdot \frac{1}{2^{11}}\)\(=\frac{45}{2^{10}}\)
\(\frac{P_2}{P_1}=\frac{45\cdot 2^{10}}{10\cdot 2^{10}}=\frac{45}{10}=4,5\)
Oтвет: 4,5
6. Решите уравнение: \( \sin \frac{\pi x}{6}=-\frac{1}{2}.\)
В ответе запишите наименьший положительный корень.
Pешение:
Замена: \(\frac{\pi x}{6}=t\)
\(\sin t=-\frac{1}{2}\)⇔\(\left[\begin{array}{ccc}t=-\frac{5\pi }{6}+2\pi n; n\in Z\\t=-\frac{\pi }{6}+2\pi n; n\in Z
\end{array}\right. \\\)
\(\left[\begin{array}{ccc}\frac{\pi x }{6}=-\frac{5\pi }{6}+2\pi n; n\in Z\\\frac{\pi x}{6}=-\frac{\pi }{6}+2\pi n; n\in Z
\end{array}\right. \\\)
Каждое уравнение умножим на \(\frac{6}{\pi}\):
\(\left[\begin{array}{ccc}x=-5+12n; n\in Z\\x=-1+12n; n\in Z
\end{array}\right. \\\)
Из каждой серии выпишем несколько значений \(x\):
\(n=0\); \(x_1=-5\); \(x_2=-1\)
\(n=1\); \(x_1=7\); \(x_2=11\)
\(n=2\); \(x_1=19\); \(x_2=23\)
наименьший положительный корень \(x=7\)
Oтвет: 7
7. Найдите значение выражения \(\frac{(b^{\sqrt{3}})^{2\sqrt{3}}}{b^4}\) при \(b=5\).
Pешение:
\(\frac{(b^{\sqrt{3}})^{2\sqrt{3}}}{b^4}=\frac{b^{\sqrt{3} \cdot 2\sqrt{3}}}{b^4}=\frac{b^6}{4}=b^2\)
При \(b=5\) получим: \(5^2=25\).
Oтвет: 25
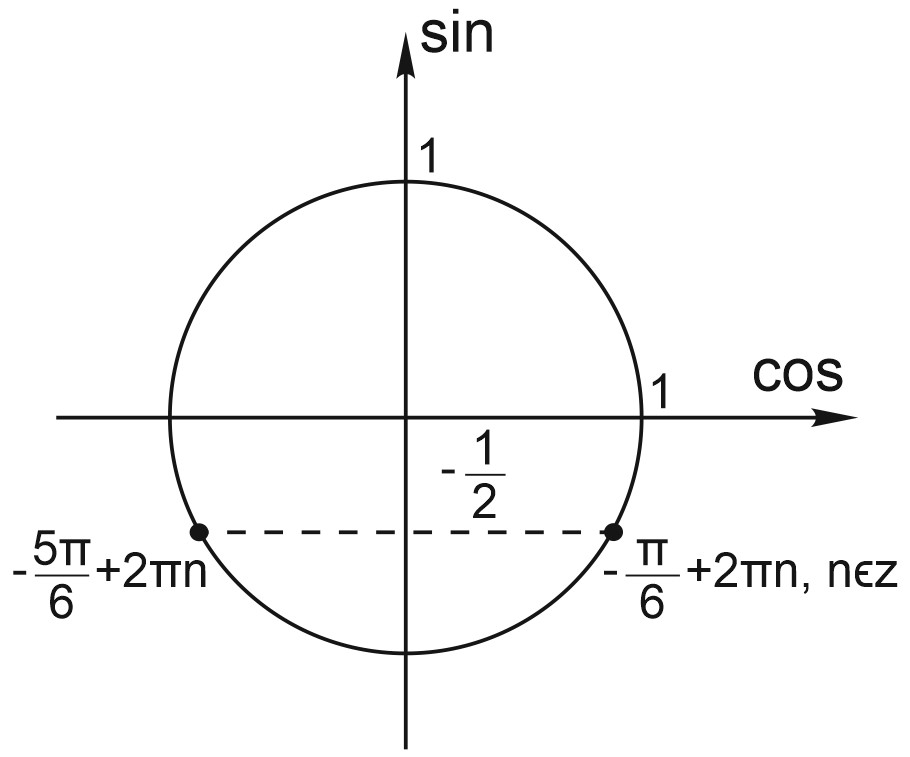
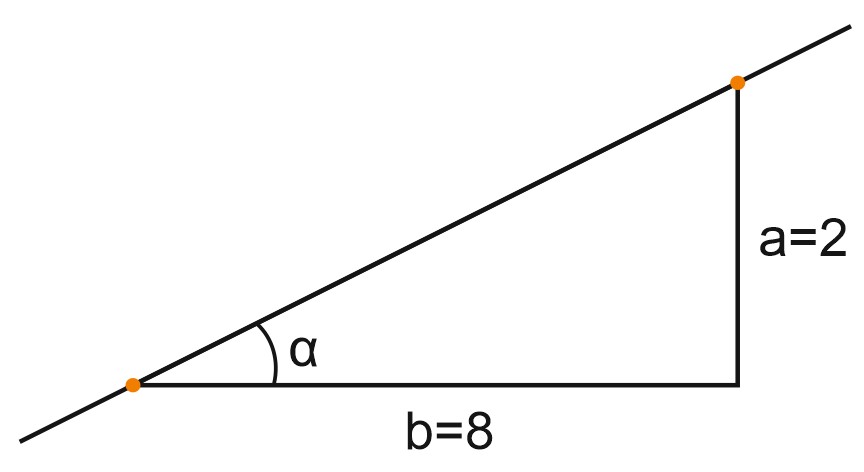
8. На рисунке изображён график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
Pешение:
На рисунке изображен график функции \(y=f(x)\)
Производная функции в точке равна тангенсу угла наклона касательной, то есть угловому коэффициенту касательной.
\(f'(x)=tg\alpha=k\)
Найдем \(tg\alpha\) из прямоугольного треугольника. Вершины острых углов – это жирные точки на рисунке.
\(tg\alpha=\frac{a}{b}=\frac{2}{8}=\frac{1}{4}=0,25\)
Oтвет: 0,25
9. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием \(f=30\) см.
Расстояние \(d_1\) от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние \(d_2\) от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение \(\frac{1}{d_1}+\frac{1}{d_2}=\frac{1}{f}\) Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.
Решение:
Фокусное расстояние линзы известно. Но какое же значение \(d_2\) (расстояние от линзы до экрана) надо подставлять в формулу? Нам надо найти наименьшее расстояние от лампочки до линзы \(d_1\). Если \(d_1\) – наименьшее, то обратная величина \(\frac{1}{d_1}\) будет наибольшей. Поскольку \(\frac{1}{f}\) – константа, второе слагаемое \(\frac{1}{d_2}\) в формуле линзы должно быть наименьшим, а обратная ему величина \(d_2\) – наибольшей, то есть равной 180. Подставим данные в формулу:
\(\frac{1}{d_2}+\frac{1}{180}=\frac{1}{30}\)
\(d_1=36\)
Oтвет: 36
10. Весной катер идёт против течения реки в \(\frac{5}{3}\) раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в \(\frac{3}{2}\) раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Pешение:
Пусть \(x\) км/ч – собственная скорость катера, \(y\) км/ч – скорость течения реки весной, \(y-1\) км/ч – скорость течения реки летом.
Составим таблицу, в которую запишем скорость движения по течению и против течения весной и летом.
Составим систему уравнений и решим ее.
\(\left\{\begin{matrix}
\frac{x+y}{x-y}=\frac{5}{3} \\
\frac{x+y-1}{x-y+1}=\frac{3}{2}\end{matrix}\right.\)
Первое уравнение: поделили скорость движения весной по течению на скорость движения весной против течения, получили \(\frac{5}{3}\).
Второе уравнение: поделили скорость движения летом по течению на скорость движения летом против течения, получили \(\frac{3}{2}\).
Каждое уравнение упростим как пропорцию.
\(\left\{\begin{matrix}
3(x+y)=5(x-y), \\
2(x+y-1)=3(x-y+1) \end{matrix}\right.\)
Раскроем скобки и приведем подобные.
\(\left\{\begin{matrix}
x=4y, \\
x-5y=-5 \end{matrix}\right.\)
Подставим \(x=4y\) во второе уравнение.
Получим: \(y=5\), это скорость течения весной.
\(x=20\).
В ответе запишем скорость течения весной.
Oтвет: 5
11. На рисунке изображены графики функций \(f(x)=\frac{k}{x}\) и \(g(x)=ax+b\), которые пересекаются в точках А и В. Найдите абсциссу точки В.
Pешение:
График функции \(y=\frac{k}{x}\) проходит через точку А(2; 1); значит, \(\frac{k}{2}=1\); \( k=2\), \( f(x)=\frac{2}{x}\).
График функции \(g(x)=ax+b\) проходит через точки (2; 1) и (1; -4), \(a=5\) – угловой коэффициент прямой; (находим как тангенс угла наклона прямой к положительному направлению оси X); тогда \(5\cdot2+b=1\); \(b=-9\).
Для точек A и B имеем: \(f(x)=g(x)\);
\(\frac{2}{x}=5x-9\);
\(5x^2-9x-2=0\);
Отсюда \(x=2\) (абсцисса точки A) или \(x=-0,2\) (абсцисса точки B).
Ответ: -0,2
12. Анна Малкова
Найдите наименьшее значение функции \( y=13+\frac{\sqrt{3} \pi}{3}-2\sqrt{3}\cdot x -4\sqrt{3} \cos x \) на отрезке \( [0;\frac{\pi}{2}]. \)
Pешение:
Найдем производную функции и приравняем ее к нулю.
\(y'=(13+\frac{\sqrt{3} \pi}{3}-2\sqrt{3}\cdot x -4\sqrt{3} \cos x)'=-2\sqrt{3}+4\sqrt{3} sin x= 2\sqrt{3}(2 sin x - 1).\)
\(y'=0\), тогда \(sin x =\frac{1}{2}\).
На указанном отрезке это уравнение имеет единственное решение \(x=\frac{\pi}{6}\).
Слева от этой точки \(2 sin x-1\) < 0, производная отрицательна. Справа от этой точки \(2 sin x-1\) > 0, производная положительна. Значит, \(x=\frac{\pi}{6}\) - точка минимума функции, и наименьшее значение функции на отрезке достигается в этой точке.
Найдем значения функции в этой точке:
\(y(\frac{\pi}{6})=13+\frac{\sqrt{3 \pi}}{3}-2\sqrt{3}\cdot \frac{\pi}{6}-4\sqrt{3}\cdot cos \frac{\pi}{6}=13+\frac{\sqrt{3 \pi}}{3}-\frac{\sqrt{3} \pi}{3}-4\sqrt{3}\cdot \frac{\sqrt{3}}{2}=13-6=7\)
Oтвет: 7
Часть 2. Задания с развернyтым ответом
13.
а) Решите уравнение \(\sin^2 2x=\cos 2x+ 4 sin^4 x\)
б) Найдите все корни уравнения на отрезке \([0;\frac{\pi}{2}].\)
Pешение:
Воспользуемся формулой понижения степени: \(sin^2 x=\frac{1-cos 2x}{2}\)
\(sin^4x=(\frac{1-cos2x}{2})^2=\frac{1-2cos2x+cos^2 2x}{4}\)
\(sin^2 2x=cos 2x+4sin^4 x\)⇔
⇔\(1-cos^2 2x=cos 2x + \frac{4(1-2cos2x+cos^2 2x)}{4}\)⇔
⇔\(1-cos^2 2x=cos 2x + 1-2cos 2x +cos^2 2x\)⇔
⇔\(2cos^2 2x - cos 2x=0\)⇔\(cos2x(2cos2x-1)=0\)⇔\(\left[\begin{array}{ccc}cos2x=0\\2cos2x=1
\end{array}\right. \\\)⇔
⇔\(\left[\begin{array}{ccc}cos2x=0\\cos2x=\frac{1}{2}
\end{array}\right. \\\)⇔\(\left[\begin{array}{ccc}2x=\frac{\pi }{2}+\pi k; k\in Z\\2x=\pm \frac{\pi }{3}+2\pi n; n\in Z\end{array}\right. \\\)⇔\(\left[\begin{array}{ccc}x=\frac{\pi }{4}+\frac{\pi k}{2}; k\in Z\\x=\pm \frac{\pi }{6}+\pi n; n\in Z\end{array}\right. \\\)
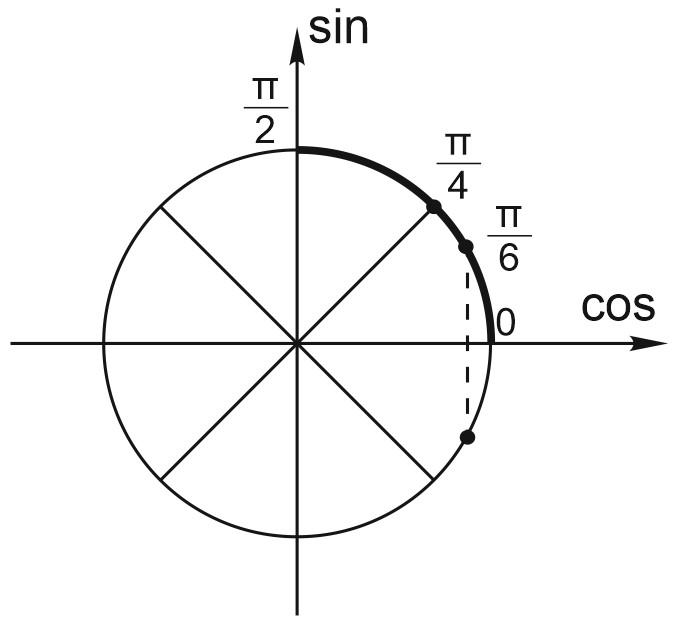
б) Найдем корни на отрезке \([0; \frac{\pi}{2}]\) с помощью единичной окружности.
Отметим на единичной окружности отрезок \([0; \frac{\pi}{2}]\) и найденные серии решений.
Видим, что указанному отрезку принадлежат точки:
\(\frac{\pi}{6}\); \(\frac{\pi}{4}\)
Oтвет: а)\(\left[\begin{array}{ccc}x=\frac{\pi }{4}+\frac{\pi k}{2}; k\in Z\\x=\pm \frac{\pi }{6}+\pi n; n\in Z\end{array}\right. \\\)
б) \(\frac{\pi}{6}\); \(\frac{\pi}{4}\)
14. Анна Малкова
В правильной четырехугольной пирамиде \(SABCD\) боковое ребро в \(\sqrt{2}\) больше, чем высота \(SO\).
а) Докажите, что все боковые грани пирамиды – правильные треугольники.
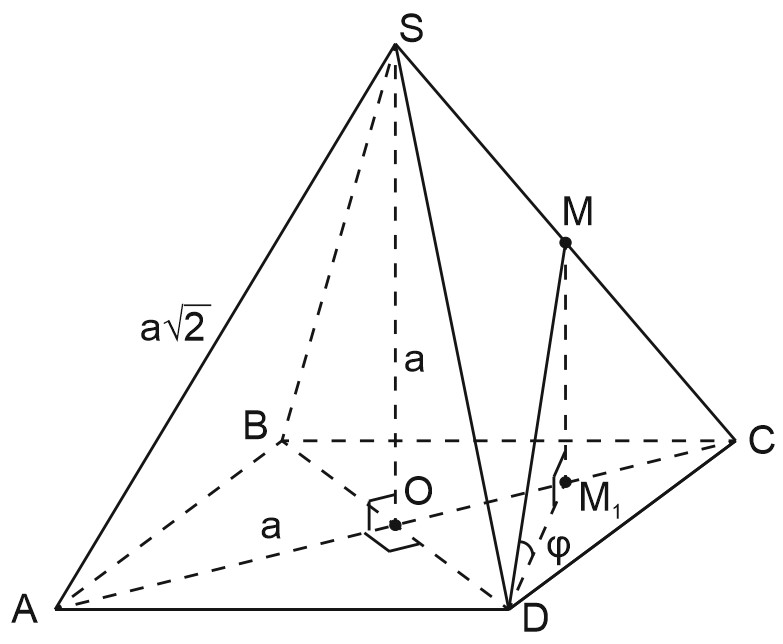
б) Точка \(M\) – середина бокового ребра \(SC\). Найдите угол между прямой \(DM\) и плоскостью основания.
Pешение:
а) \(SABCD\) - правильная четырехугольная пирамида, основание пирамиды \(ABCD\) - квадрат, высота пирамиды проецируется в центр квадрата, а боковые грани - равные равнобедренные треугольники.
Пусть \(SO=a\), тогда \(SA=a\sqrt{2}\),
\(\triangle SOA\) – прямоугольный. По теореме Пифагора получаем, что \(AO=a\).
\(ABCD\) – квадрат, диагонали квадрата равны и взаимно перпендикулярны, точкой пересечения делятся пополам. Значит, \( AO=OD=a\),
\(\triangle AOD\) – прямоугольный, равнобедренный, \(AD=a\sqrt{2}\).
Получили для \(\bigtriangleup SAD\): \(SA=SD=AD=a\sqrt{2}\);
\(\triangle SAD\) –правильный, и все боковые грани правильные треугольники.
б) \(M\) – середина бокового ребра \(SC\), тогда \(SM=MC\).
Пусть \(M_1\) –проекция точки \(M\) на плоскость \((ABC)\).
\(MM_1 \perp (ABC)\)⇒\(MM_1\parallel SO\), а значит, \(M_1\) – середина \(OC\) (т.к. \(\triangle MM_1C~\triangle SOC\) по двум углам).
\(MM_1=\frac{a}{2}\). Найдём \(DM_1\).
\(\triangle ODM_1\) прямоугольный, \(OM=\frac{a}{2}\); \(OD=a\)
\(DM_1=\sqrt{OM_1^2+OD^2}=\sqrt{a^2+(\frac{a}{2})^2}=\frac{a\sqrt{5}}{2}\).
Угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость. Угол между прямой \(MD\) и плоскостью основания – это угол \(\angle MDM_1=\varphi \).
Рассмотрим прямоугольный треугольник \(MDM_1\).
\(tg \varphi=\frac{MM_1}{DM_1}=\frac{a}{2}:\frac{a\sqrt{5}}{2}=\frac{1}{\sqrt{5}}\);
Также можно было найти синус угла \(\varphi\).
В равностороннем треугольнике \(SDCDM\)- медиана и высота,
\(DM=\frac{a\sqrt{6}}{2}\).
\(sin\) \(\varphi \)=\(\frac{MM_1}{DM}\)=\(\frac{a}{2}:\frac{a\sqrt{6}}{2}=\frac{1}{\sqrt{6}}\)⇒\(\varphi=arcsin \frac{1}{\sqrt{6}}\).
Ответ: \(\varphi=arcsin \frac{1}{\sqrt{6}}=arctg \frac{1}{\sqrt{5}}\)
15. Решите неравенство: \(log_{0,5}(x^2+3x-2)+log_{2}(x^4+6x^3+9x^2)\leqslant 3\).
Решение:
Упростим выражение под вторым логарифмом.
\(x^4+6x^3+9x^2=x^2(x^2+6x+9)=x^2\cdot (x+3)^2=(x\cdot (x+3))^2=(x^2+3x)^2\)
Неравенство примет вид:
\(log_{0,5}(x^2+3x-2)+log_2(x^2+3x)^2\leqslant 3\)
\( log_{0,5}(x^2+3x-2)=-log_2(x^2+3x-2) \)
Сделаем замену переменной: \(x^2+3x=t\)
\(log_2 t^2\leqslant 3+log_2(t-2)\)⇔
⇔\(\left\{\begin{matrix}
t^2>0 \\
t-2>0 \\
log_2 t^2\leqslant log_2 (8t-16)\end{matrix}\right.\)
Функция \(y=log_2 z\) монотонно возрастает, и если \(log_2 z_1 \leqslant log_2 z_2\),то \(z_1\leqslant z_2\).
\(\left\{\begin{matrix}
t\neq 0 \\
t>2 \\
t^2-8t+16\leqslant 0 \end{matrix}\right.\)⇔\(\left\{\begin{matrix}
t\neq 0 \\
t>2 \\
(t-4)^2\leqslant 0 \end{matrix}\right.\)⇔\(t=4\).
Обратная замена:
\(x^2+3x=4\)⇔\(x^2+3x-4=0\)⇔\(\left[\begin{array}{ccc}x=1\\x=-4\end{array}\right. \\\)
Ответ: -4;1
16. Анна Малкова
Программист Егор покупает квартиру в ипотеку под 25% годовых. Егор рассчитал, что если выплачивать кредит ежегодными платежами, составляющими 738 тысяч рублей, кредит будет полностью выплачен за 3 года. Какими должны быть ежегодные платежи, чтобы Егор смог выплатить ипотечный кредит за 4 года?
Pешение:
Напишем схему погашения кредита.
Если Егор выплатит кредит за 3 года ежегодными платежами \(X=738\) тысяч рублей, получим:
\(((S\cdot k-X)\cdot k-X)\cdot k-X=0\)
Раскроем скобки:
\(Sk^3-X(k^2+k+1)=0\);
\(X=\frac{S \cdot k^3}{k^2+k+1}\) (1). Будем вести расчеты в тысячах рублей.
Если Егор выплатит кредит за 4 года ежегодными платежами Y, получим:
\((((S \cdot k-Y) \cdot k-Y) \cdot k-Y) \cdot k-Y=0\)
\(Sk^4-Y(k^3+k^2+k+1)=0\);
\(Y=\frac{S \cdot k^4}{k^3+k^2+k+1}\) (2)
Поделим второе уравнение на первое.
\(\frac{Y}{X}=\frac{k(k^2+k+1)}{(k^2+1)(k+1)}\)
\(\frac{Y}{X}=\frac{k(k^2+k+1)(k-1)}{(k^2+1)(k+1)(k-1)}\)
Применим формулы разности кубов и разности квадратов.
\(\frac{Y}{X}=\frac{k(k^3-1)}{(k^4-1)}=\frac{5(5^3-4^3)}{(5^4-4^4)}=\frac{5(125-64)}{625-256}=\frac{305}{369}\),
\(Y=\frac{305}{369}\cdot 738=610\)
Ответ: 610
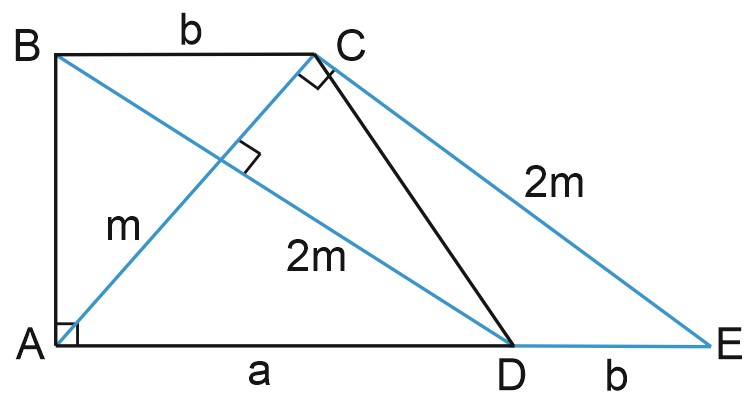
17. В прямоугольной трапеции \(ABCD\) с основаниями \(AD\) и \(BC\) диагонали \(AC\) и \(BD\) взаимно перпендикулярны, отношение \(BD:AC=2\).
а) Докажите, что площадь трапеции равна площади квадрата со стороной \(AC\).
б) Найдите отношение \(AD\) к \(BC\).
Pешение:
а) \(S\) трапеции = \(S\) квадрата =\(AC^2\)
Пусть \(AC=m\), \(BD=2m\)
Проведем \( CE\parallel BD\),
\(BC\) и \(ED\) - параллельные прямые по определению,
\(BC=ED\), \( BD\parallel CE\);
\(AD=a\), \(DE=BC=b\);
\(\triangle ACE\) - прямоугольный;
\(S_{\triangle ACE}=\frac{1}{2}AC\cdot CE=\frac{1}{2}m\cdot 2m=\frac{a+b}{2}\cdot h=S\) трапеции
б)
1) Обозначим: \(AD=a\); \(BC=b\); \(AC=m\);
\(BD=2m\). Проведем \(CE\parallel BD\) и продолжим \(AD\) до точки \(E\). Тогда \(BCED\) – параллелограмм и \(CE=2m\), \(DE=b\).
2) Найдем соотношения между \(a,b,m\), используя прямоугольные треугольники.
Из \(\triangle ACE\): \((a+b)^2=m^2+(2m)^2=5m^2\). Отсюда: \(m^2=\frac{(a+b)^2}{5}\) (1)
Из \(\triangle ABC\):\(AB^2=m^2-b^2\), а из \(\triangle ABD\):\(AB^2=4m^2-a^2\). Отсюда:
\(m^2-b^2=4m^2-a^2\), или \(a^2-b^2=3m^2\), или \(m^2=\frac{a^2-b^2}{3}\) (2)
Из (1) и (2) получаем: \(\frac{(a+b)^2}{5}=\frac{(a+b)(a-b)}{3}\); \(3(a+b)=5(a-b)\); \(a=4b\). Отношение оснований трапеции равно 4.
Ответ: 4
18. Анна Малкова
При каких значениях параметра \(a\) система
\(\left\{\begin{matrix}
(a-x-2)(a+x-4)=0 \\
x^2+a^2\leqslant 4x+6a\end{matrix}\right.\)
имеет единственное решение?
Pешение:
Первое уравнение: произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другие при этом имеют смысл. Значит, первое уравнение равносильно совокупности уравнений:
\(\left[\begin{array}{ccc}a=x+2\\a=-x+4\end{array}\right. \\\)
На плоскости \((x; a)\) такая совокупность задает пару пересекающихся прямых.
Второе неравенство: \(x^2+a^2\leqslant 4x+6a\)
Перенесем все слагаемые в левую часть неравенства и выделим полные квадраты.
\(x^2-4x+4+a^2-6a+9\leqslant 13\)
\((x-2)^2+(a-3)^2\leqslant 13\)
На координатной плоскости \((x; a)\) это неравенство задает круг вместе с границей с центром в точке \(P(2;3)\) и радиусом равным \(\sqrt{13}\).
Получили систему:
\(\left\{\begin{matrix}
\left[\begin{array}{ccc}a=x+2\\a=-x+4\end{array}\right. \\ \\
(x-2)^2+(a-3)^2\leqslant 13\end{matrix}\right.\)
Решаем систему графически.
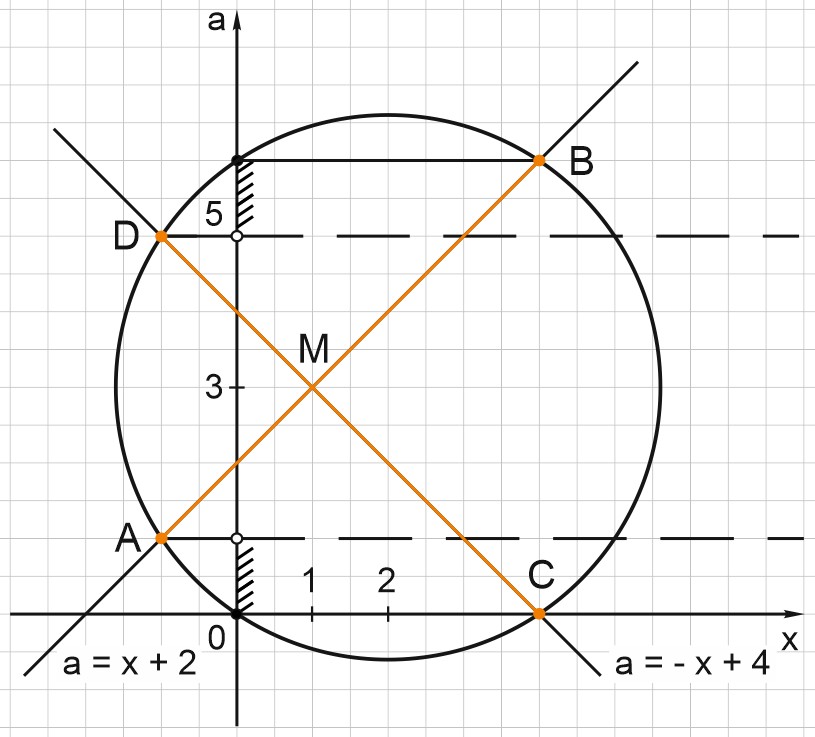
Заметим, что точка \(O(0;0)\) лежит на окружности \((x-2)^2+(a-3)^2=13\), так как квадрат расстояния от точки \(P(2;3)\) до начала координат равен \(2^2+3^2=13\).
Точки \(A(-1;1)\); \(B(4;6)\); \(C(4;0)\) и \(D(-1;5)\) также лежат на этой окружности. В этом легко убедиться, подставив координаты этих точек в уравнение окружности
\((x-2)^2+(a-3)^2=13\).
Прямая \(a=x+2\) проходит через точки \(A(-1;1)\) и \(B(4;6)\).
Прямая \(a=-x+4\) проходит через точки \(C(4;0)\) и \(D(-1;5)\).
Прямые \(a=x+2\) и \(a=-x+4\) пересекаются в точке \(M(1;3)\).
Решениями системы являются пары чисел \((x;y)\), соответствующие координатам точек, лежащих хотя бы на одной из данных прямых и при этом внутри круга (или на его границе).
Система имеет ровно одно решение, если круг и совокупность прямых имеют ровно одну общую точку.
Это происходит в следующих случаях:
1) Прямая \(a = a_0\) проходит выше точки \(C\) или через точку \(C\) и ниже точки \(A\). Это значит, что \(a\in [0;1)\).
2) Прямая \(a = a_0\) проходит через точку \(M\) пересечения прямых \(a=x+2\) и \(a=-x+4\). Это значит, что \(a=3\) (ордината точки \(M\) равна 3).
Прямая \(a=a_0\) проходит выше точки \(D\) или через точку \(D\). При этом \(a \in (5;6]\).
Ответ: \(a\in [0;1)\cup {{{3}}}\cup (5;6]\)
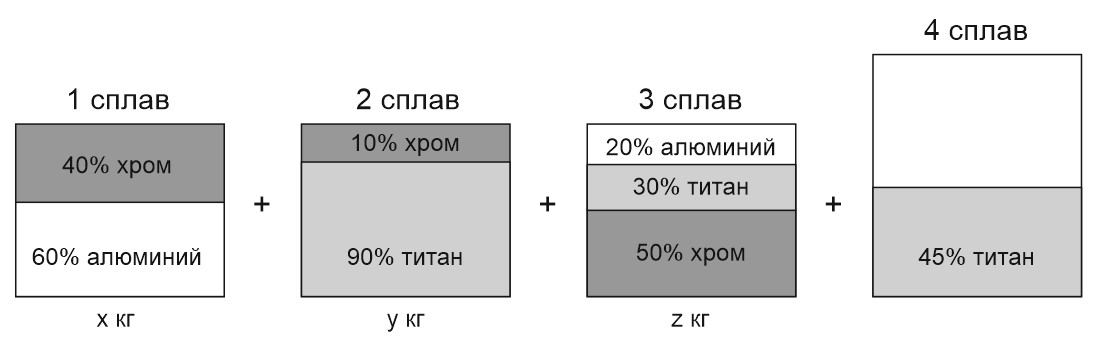
19. Даны три сплава. Состав первого: 60% алюминия, 40% хрома.
Состав второго: 10% хрома, 90% титана.
Состав третьего сплава: 20% алюминия, 50% хрома, 30% титана.
Из них нужно приготовить новый сплав, содержащий 45% титана.
Известно, что массы всех трех сплавов выражаются целыми числами.
а) Может ли масса третьего сплава быть равной 7 кг?
б) Может ли процентное содержание хрома в новом сплаве быть равным 42%?
в) Найдите наименьшее процентное содержание хрома в новом сплаве. Ответ выразите в процентах.
Решение:
Пусть \(x\) кг – масса первого сплава, \(y\) кг – масса второго сплава, \(z\) кг – масса третьего.
Тогда их сумма \(x+y+z\) кг – масса четвертого сплава.
Пусть в четвертом сплаве содержится \(p\)% хрома. Запишем систему уравнений:
\(\left\{\begin{matrix}
0,4x+0,1y+0,5z=p(x+y+z) (1) \\
0,9y+0,3z=0,45(x+y+z) (2) \end{matrix}\right.\)
(1) - для хрома
(2) - для титана
Умножим каждое из уравнений на 10, чтобы избавиться от дробных коэффициентов.
\(\left\{\begin{matrix}
4x+y+5z=10p(x+y+z) \\
90y+30z=45x+45y+45y \end{matrix}\right.\)
\(\left\{\begin{matrix}
4x+y+5z=10p(x+y+z) \\
3y=3x+z \end{matrix}\right.\)
Из второго уравнения выразим \(z=3y-3x\).
а) Так как \(z=3y-3x\), \(z\) делится на 3, значит, \(z\) не может быть равно 7.
б) Заметим, что, поскольку \(z\geqslant 0\), должно выполняться условие \(y\geqslant x\).
Из первого уравнения выразим 10р.
\(10p=\frac{4x+y+5z}{x+y+z}=\frac{16y-11x}{4y-2x}\).
Умножим обе части этого уравнения на 2. Знаменатель станет проще.
\(20p=\frac{16y-11x}{2y-x}\).
Теперь у нас есть система:
\(\left\{\begin{matrix}
20p=\frac{16y-11x}{2y-x} \\
y\geqslant x \end{matrix}\right.\)
Выделим целую часть:
\(20p=\frac{16y-8x-3x}{2y-x}=8-\frac{3x}{2y-x}\).
Очевидно, что \(\frac{3x}{2y-x}\geqslant 0\). Ведь \(x\) – неотрицательная величина, \(y \geqslant x\), и тогда \(2y-x\) в знаменателе положительна. Тогда
\(20p\leqslant 8\), \(p\leqslant \frac{8}{20}\),
то есть \(p\leqslant 40\)%.
Нет, \(p=42\)% не может быть.
в) Пусть \(t=\frac{y}{x}\), \(t\geqslant 1\), поскольку \(y\geqslant x\).
\(20p=8-\frac{3}{2t-1}\).
Поскольку \(t\geqslant 1\),
\(2t-1\geqslant 1\) и \(3/(2t-1)\leqslant 3\).Тогда
\(20p\geqslant 8-3\); \(20 p\geqslant 5\), \(p\geqslant 25\)%
Мы оценили \(p\). Осталось привести примеры, когда \(p=25\)% и когда \(p = 40\)%.
Возьмем \(x=0\) (первый сплав не берем вообще). Тогда \(z = 3y\) (масса третьего сплава в 3 раза больше, чем масса второго).
Пусть масса второго сплава равна \(m_1\), масса третьего \(3m_1\).
Для хрома: \(0,1m_1+0,5\cdot 3m_1=1,6m_1=0,4\cdot 4m_1\), то есть в четвертом сплаве 40% хрома.
Для титана: \(0,9m_1+0,3\cdot 3m=1,8m_1= 0,45\cdot 4m_1\) – в четвертом сплаве 45% титана.
Возьмем \(x=y=m_2\) (первого и второго сплава поровну). Тогда \(z=0\) (третий сплав не берем), для хрома получаем:
\(0,4\cdot m_2+0,1 m_2=0,5 \cdot m_2=0,25\cdot 2m_2\) – в итоговом сплаве 25% хрома.
Для титана: \(0,9\cdot m_2=0,45\cdot 2 m_2\) – в итоговом сплаве снова 45% титана. Все условия выполнены.
Ответ:
а) нет
б) нет
в) 25