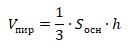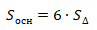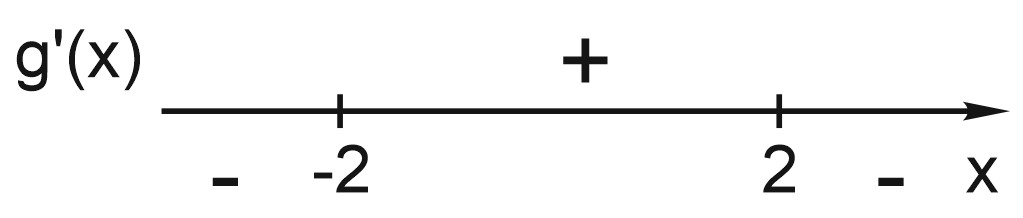ЕГЭ-2023 Вариант 3, решения

Видеоразбор: https://www.youtube.com/watch?v=pPIPqQSIxY0&t;t\&t=6712s
и https://www.youtube.com/watch?v=GFlLWF2jXBk&t;t\&t=48s

Часть 1. Задания с кратким ответом

1. Два угла вписанного в окружность четырёхугольника равны 56° и 77°. Найдите меньший из оставшихся углов. Ответ выразите в градусах.

Решение: $[(x),(x):]$

Четырехугольник вписан в окружность, поэтому сумма противолежащих углов равна 180°. Углы, равные 56° и 77°, не могут быть противоположными, их сумма не равна 180°. Значит, напротив угла в 56° лежит угол 180°-56°=124°, а напротив угла 77° лежит угол 180°-77°=103°, это меньший из оставшихся углов.

Ответ:103

2. Объем правильной пирамиды $SABCDEF$ равен 18.
Найдите объем пирамиды $SACDF$ .

Решение:

Объем пирамиды $SABCDEF$ – это $V_1=18$
Объем пирамиды $SACDF$ – это $V_2$ , его нужно найти.

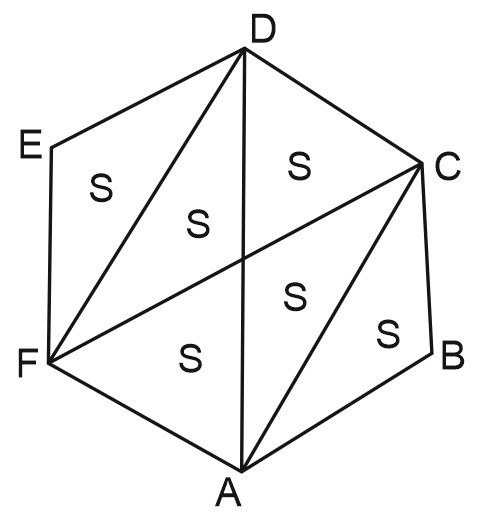
Разделим шестиугольник $ABCDEF$ на 6 треугольников, как показано на рисунке.
Заметим, что площади треугольников $AOF$ и $AOC$ равны (у них одинаковые основания и одинаковая высота).

Значит, площадь шестиугольника $ABCDEF$ в 6 раз больше площади треугольника $AOC$ , а площадь четырехугольника $ACDF$ – в 4 раза больше площади треугольника $AOC$ .

$S_{ACDF}=4S_\Delta$

$\frac{V_1}{V_2}=\frac{S_1}{S_2}=\frac{6}{4}$

$\frac{18}{V_2}=\frac{6}{4}=\frac{3}{2}$

$V_2=12$

Ответ: 12

3. Анна Малкова

Среди учащихся 11-х классов школы 100 человек сдают ЕГЭ по математике Профильного уровня. 55 из 100 готовятся к нему на курсах или с репетитором, 35 – самостоятельно, остальные не готовятся, но верят, что все будет хорошо.

По статистике, собранной за несколько лет учителем математики этой школы, вероятность написать Пробный ЕГЭ в ноябре не ниже 70 баллов равна 0,8 для тех, кто занимается на курсах или с репетитором. Для тех, кто готовится самостоятельно, вероятность написать Пробный не ниже 70 баллов равна 0,6. Для тех, кто не готовится, вероятность получить на Пробном не ниже 70 баллов равна 0,2.

В ноябре 2022 года все 100 учащихся написали Пробный ЕГЭ. Учитель математики берет на проверку случайно выбранную работу учащегося. С какой вероятностью эта работа будет оценена не ниже, чем в 70 баллов?

Решение:

Применим теоремы о сумме несовместных событий и произведении независимых событий.
Написать Пробный не ниже 70 баллов мог ученик, который занимался на курсах или с репетитором и получил не ниже 70. Или тот, кто готовился самостоятельно и получил не ниже 70. Или тот, кто не готовился и получил не ниже 70 баллов.

$p=0,55\cdot 0,8+0,35\cdot 0,6+0,02=0,44+0,21+0,02=0,67$

Ответ: 0,67

4. Анна Малкова

Предположим, что в условиях предыдущей задачи учитель математики проверил случайно выбранную работу и поставил за нее 72 балла. С какой вероятностью эта работа написана учеником, который никак не готовился к ЕГЭ по математике?
Результат округлите до сотых.

Решение:

Это задача на условную вероятность. Применим простой способ ее решения.
в задаче 3 мы нашли, что с вероятностью 0,67 работа оценена не ниже 70 баллов. Значит, 67 из 100 учеников получили не ниже 70 баллов.

Из 100 человек 10 никак не готовятся и с вероятностью 0,2 получают не ниже 70 баллов. Значит, 2 человека никак не готовились и получили не ниже 70.
Среди тех, кто никак не готовился (67 учеников), двое получили не ниже 70 баллов.
Вероятность равна $\frac{2}{67}\approx 0,03$ .

Ответ: 0,03

5. Решите уравнение: $log_2(2^x-8)=3$ .

Решение:

$log_2(2^x-8)=3$
ОДЗ: $2^x-8>0$
$2^x-8=2^3$
$2^x=16$
$x=4$

Ответ: 4

6. Александра Антонова

Найдите значение выражения: $\frac{1}{2}+8\sqrt{2}sin\frac{\pi}{8}cos\frac{\pi}{8}$ .

Решение:
Воспользуемся формулой синуса двойного угла:

$sin 2\alpha =2 sin \alpha \cdot cos\alpha$

$\frac{1}{2}+8\sqrt{2} sin \frac{\pi}{8} cos \frac{\pi}{8}=\frac{1}{2}+4\sqrt{2}\cdot sin \frac{\pi}{4}=\frac{1}{2}+4\sqrt{2}\cdot \frac{\sqrt{2}}{2}=4,5$

Ответ: 4,5

7. На рисунке изображен график производной функции $f(x)$ , определенной на отрезке [-3; 7]. В какой точке отрезка [1; 5] $f(x)$ принимает наименьшее значение?

Решение:

На рисунке изображен график производной.
Если функция возрастает – ее производная положительна. Если функция убывает – ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса на «плюс». На рисунке есть такая точка, и это $x = 1,5$ . Слева от этой точки, на отрезке [1; 1,5], производная отрицательна, и функция убывает. Справа от этой точки, на интервале [1,5; 5), производная положительна, и функция возрастает. Значит, $x=1,5$ - точка минимума функции $f(x)$ . Поэтому свое наименьшее значение функция $y = f(x)$ принимает свое наименьшее значение на данном интервале в точке 1,5

Ответ: 1,5

8. Анна Малкова
Ускорение свободного падения (в м/с²) на поверхности планеты рассчитывается по формуле $g=G\cdot \frac{M_{planety}}{(R_{planety})^2}$ , где $G$ – гравитационная постоянная, $G = 6,67\cdot 10^{-11}$ $\frac{m^{3}}{c^{2}}$ ∙кг.
Определите ускорение свободного падения на поверхности планеты Файра*, если масса Файры равна $3,68\cdot 10^{24}$ кг, ее радиус равен $4,6\cdot 10^{6}$ метров, условия на планете близки к земным.

*Название вымышленное, возможные совпадения случайны.

Решение:
Найдем ускорение свободного падения на поверхности планеты Файра, подставив данные в формулу:

$g=G\cdot \frac{M_{planety}}{(R_{planety})^2}$ =
= $6,67\cdot 10^{-11}\cdot \frac{3,68\cdot 10^{24}}{(4,6\cdot 10^6)^2}=\frac{3,68\cdot 66,7}{4,6^2}=\frac{0,8\cdot 66,7}{4,6}=11,6$

Как видим, ускорение свободного падения на поверхности Файры немногим больше земного (равного 9,8 м/с²).

Ответ: 11,6

9. Александра Антонова

Сколько граммов воды нужно добавить к 50 граммов сухого картофельного пюре с содержанием воды 7%, чтобы получить пюре с содержанием воды 85%?

Решение:

Сухое пюре содержит воду и «сухой ингредиент», причем сухого ингредиента в нем 93%. Содержание сухого ингредиента в готовом пюре составляет 15%. При добавлении воды масса сухого ингредиента не меняется. Примем массу готового пюре за $x$ и составим уравнение:
$0,93\cdot 50 = 0,15x$ .
Отсюда $x = 310$ граммов – масса готового пюре. Значит, добавить надо $310-50=260$ граммов воды.

Ответ: 260

10. На рисунке изображены графики функций $f(x)=a\sqrt{x}$ и $g(x)=kx+b$ , которые пересекаются в точке А. Найдите ординату точки А.

Решение:

1) Найдем уравнение линейной функции. На ее графике выделены точки (3;2) и (6;1).
Линейная функция на рисунке - убывающая, значит, $k<0$ .
$k=tg \alpha =-\frac{1}{3}$ – угловой коэффициент прямой.

Формула линейной функции: $y=-\frac{1}{3}x+b$ . Чтобы найти $b$ , подставим в эту формулу координаты любой из выделенных точек. Возьмем, например, точку (3;2).

$2=-\frac{1}{3}\cdot 3+b$ ; $b=3$

$y=-\frac{1}{3}x+3$ - формула линейной функции.

2) Найдем коэффициент $a$ в формуле второй функции $f(x)=a\sqrt{x}$ . На ее графике выделена точка (4;-3).
Подставим координаты этой точки в уравнение:
$-3=a\sqrt{4}$ ; $a=-1,5$ ; $f(x)=-1,5\sqrt{x}$ .

3) Найдем точки пересечения графиков функций. Для этого решим систему уравнений:

$\left\{\begin{matrix}y=-\frac{1}{3}x+3 \\y=-1,5\sqrt{x}\end{matrix}\right.$

$-1,5\sqrt{x}=-\frac{1}{3}x+3$ ;

$9\sqrt{x}=2x-18$

Решив это уравнение, найдем, что $x=36$ .

Это абсцисса точки пересечения графиков. Найдем ординату этой точки.

$y(36)=-1,5\sqrt{36} = -1,5\cdot 6=-9$

Ответ: -9

11. Анна Малкова

Найдите наименьшее значение функции $g(x)=\frac{x}{x^2+4}$ на отрезке $[1;3].$

Решение:

Эта функция определена для всех $x$ и является нечетной.
Если $x < 0$ , значения функции отрицательны. Если $x> 0$ , значения функции положительны.
Найдем производную функции: $g$ , $g$ , если $x=\pm 2$

Исследуем знаки производной:

На отрезке [1;3] есть только точка максимума $x=2$ . Найдем значения функции на концах этого отрезка.

$g(1)=0,2;$ $g(3)=\frac{3}{13}.$

Сравним 0,2 и $\frac{3}{13}$

$\frac{1}{5}\vee \frac{3}{13}$

$13<15$

$0,2 < \frac{3}{13}$

Значит, наименьшее значение на отрезке равно 0,2.

Ответ: 0,2

Часть 2. Задания с развернутым ответом

12.

а) Решите уравнение: $sin 2x sin 6x = cos x cos 3x$

б) Найдите все корни уравнения на отрезке $[0;\frac{\pi}{2} ].$

Решение:

Пользуемся формулами преобразования произведения в сумму.

Домножим обе части на 2, преобразуем левую часть в разность косинусов, а правую часть — в сумму косинусов:

$2sin 2x sin 6x= 2 cos x cos 3x$

$cos 4x - cos 8x=cos 2x +cos4x$

$cos 2x + cos 8x=0$

$2 cos 5x cos 3x = 0$

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, а другой при этом имеет смысл.

Получим: $cos5x=0$ или $cos3x=0$ Отсюда

$x_1=\frac{\pi}{10}+\frac{\pi n}{5},$ $x_2=\frac{\pi}{6}+\frac{\pi n}{3},$ $n\in Z$

б) Найдем корни на отрезке [0; $\frac{\pi}{2}$ ] с помощью двойного неравенства.

1) $x_1=\frac{\pi}{10}+\frac{\pi n}{5},$ $n\in Z$

$0\leqslant \frac{\pi}{10}+\frac{\pi k}{5}\leqslant \frac{\pi}{2}$

$0\leqslant \frac{1}{10}+\frac{k}{5}\leqslant \frac{1}{2}$

$0\leqslant \frac{1}{2}+ k \leqslant \frac{5}{2}$

$-\frac{1}{2}\leqslant k \leqslant 2$

$k=0;1;2.$

$x_1=\frac{\pi}{10}$

$x_2=\frac{\pi}{10}+\frac{\pi}{5}=\frac{3 \pi}{10}$

$x_3=\frac{\pi}{10}+\frac{2 \pi}{5}=\frac{\pi}{2}$

2) $x_2=\frac{\pi}{6}+\frac{\pi n}{3},$ $n\in Z$

$0\leqslant \frac{\pi}{6}+\frac{\pi n}{3}\leqslant \frac{\pi}{2}$

$0\leqslant \frac{1}{6}+\frac{n}{3}\leqslant \frac{1}{2}$

$0\leqslant \frac{1}{2}+n \leqslant \frac{3}{2}$

$-\frac{1}{2}\leqslant n \leqslant 1$

$n=0$ или $n=1$

$x=\frac{\pi}{6}$ или $x=\frac{\pi}{2}$

Ответ: а) $x_1=\frac{\pi}{10}+\frac{\pi n}{5},$ $x_2=\frac{\pi}{6}+\frac{\pi n}{3},$ $n\in Z$

б) $\frac{\pi}{10}; \frac{\pi}{6}; \frac{3 \pi}{10}; \frac{\pi}{2}$

13. Анна Малкова

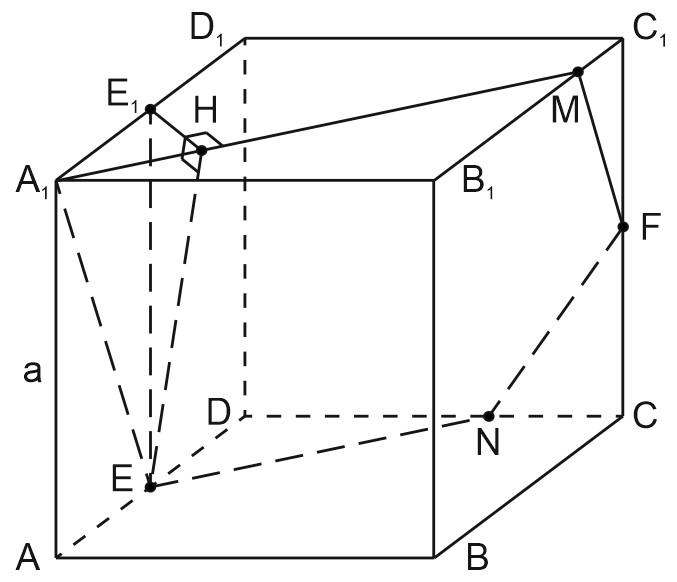
Дан куб $A...D_1$ . Точка $E$ – середина ребра $AD$ , точка $F$ – середина ребра $CC_1$ . Плоскость, проходящая через точки $E, F$ и $A_1$ , пересекает ребро $CD$ в точке $N$ .
а) Докажите, что $DN :CN = 2 : 1$ .
б) Найдите угол между плоскостью сечения и плоскостью основания куба. В ответе запишите тангенс этого угла.

Решение:

a) Докажем, что $DN:CN=2:1$ .

Построим сечение куба плоскостью $\alpha$ .

$A_1$ и $E$ лежат в плоскости $AA_1 D$ и в плоскости $\alpha$ , $A_1 E$ - линия пересечения плоскостей $AA_1 D$ и $\alpha$ .

Линии пересечения параллельных плоскостей третьей плоскостью параллельны, поэтому
плоскость сечения пересекает противоположные грани куба по параллельным прямым.

Пусть точка $T$ – середина $B_1 C_1$ , тогда $CT \parallel A_1 E$ и $CT=A_1 E$ , т.к. $\triangle A_1 E A= \triangle CTC_1$ .

Обозначим ребро куба $a$ .

Пусть $M$ - середина $TC_1$ , тогда $MF$ - средняя линия $\triangle CTC_1$ , $MF\parallel CT$ ,
$MC_1=\frac{1}{4} B_1 C_1$ .

Построим $EN\parallel A_1 M$ ;

Получим $A_1 ENFM$ - сечение куба плоскостью $\alpha$ .

$\triangle DNE \sim \triangle B_1 A_1 M$ ⇒

$\frac{DE}{B_1M}=\frac{DN}{A_1B_1}$

$\frac{a\cdot 4}{2\cdot 3a}=\frac{x}{a}$

$\frac{x}{a}=\frac{2}{3}$

$x=\frac{2}{3}aDN=\frac{2}{3}a$

$CN=\frac{1}{3}a$

$DN:CN=2:1.$

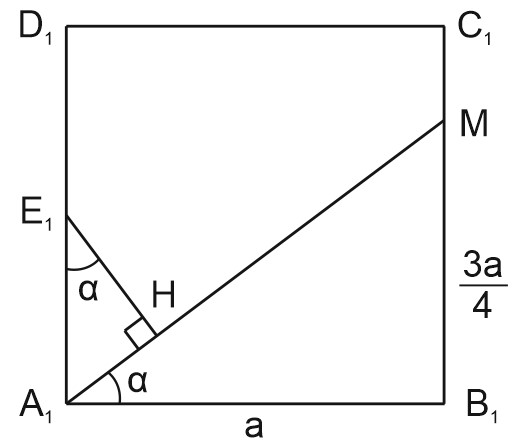
б) Найдем угол $\varphi$ между плоскостями $(A_1 EF)$ и $(ABC)$ . Он равен углу между плоскостями $(A_1 EF)$ и $(A_1 B_1 C_1 )$ , так как плоскости $(ABC)$ и $(A_1 B_1 C_1)$ параллельны.

Пусть $E_1$ – проекция точки $E$ на плоскость $(A_1 B_1 C_1 )$ ,
$E_1 H\perp A_1 M$ , тогда $EH\perp A_1 M$ по теореме о трёх перпендикулярах.

$\triangle E_1 HA \sim \triangle AB_1 M$ по двум углам,

$\frac{E_1H}{A_1B_1}=\frac{AE_1}{A_1M}$

Из прямоугольного треугольника $\triangle A_1B_1M:A_1M=\frac{5a}{4}$ . Тогда

$\frac{E_1H}{a}=\frac{a\cdot 4}{2\cdot 5a}$

$E_1H=a\cdot\frac{2}{5}$

$tg\varphi =\frac{EE_1}{E_1H}=\frac{a\cdot 5}{a\cdot 2}=\frac{5}{2}=2,5$

Ответ: 2,5

14. Александра Антонова

Решите неравенство: $log_7(49x^2-25)-log_7 x\leqslant log_7(50x-\frac{9}{x}-10)$ .

Решение:

Неравенство равносильно системе:

$\left\{\begin{matrix}49x^2-25>0 \\x>0 \\50x-\frac{9}{x}-10>0 \\log_7\frac{49x^2-25}{x}\leqslant log_7(50x-\frac{9}{x}-10)\end{matrix}\right.$

Функция $y = log_7 t$ монотонно возрастает, потому что основание логарифма больше единицы. Поэтому
$log_7 t_1 \le log_7 t_2$ ⇔ $t_1\le t_2$ при $t_1>0$ , $t_2>0$ .

Система примет вид:

$\left\{\begin{matrix}(7x-5)\cdot (7x+5)>0 \\x>0 \\50x^2-10x-9>0 \\49x^2-25\leqslant 50x^2-10x-9\end{matrix}\right.$

Третье неравенство следует из первого и четвертого.
Система становится проще:

$\left\{\begin{matrix}7x-5>0 \\x>0 \\x^2-10x+16\geqslant 0\end{matrix}\right.$ ⇔ $\left\{\begin{matrix}x>\frac{5}{7} \\(x-8)\cdot (x-2)\geqslant 0\end{matrix}\right.$

Решим последнее неравенство. Для этого найдем корни уравнения

$x^2-10x+16=0$ . Это $x=2$ или $x=8$ .

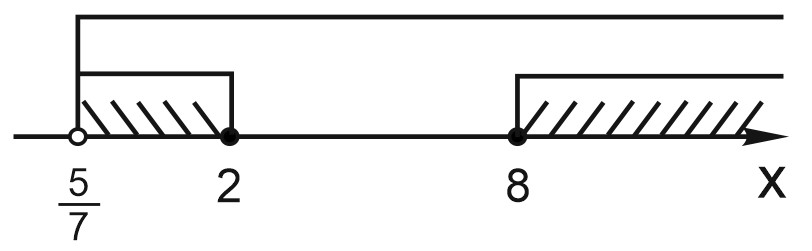
Отметим на числовой прямой решения неравенств системы и запишем ответ.

Ответ: $(\frac{5}{7};2]\cup [8;+\infty ]$

15. Анна Малкова

Задумав разбогатеть, Валентина Петровна основала стартап под названием «Всем банан».
1 ноября Валентина Петровна закупила 2 тонны бананов. Ежедневно с утра, начиная со 2 ноября, она развозит их по отдаленным деревням и продает по цене, в 5 раз превышающей закупочную.
Заботясь о потребителе, Валентина Петровна каждое утро, начиная со 2 ноября, перед началом торговли проверяет состояние бананов и находит, что 10% из них испортились и не годятся для продажи. Валентина Петровна выбрасывает испорченные бананы и продает хорошие, причем каждый день ей удается продать 250 кг бананов.
Сколько дней Валентине Петровне придется с утра продавать бананы, чтобы распродать все 2 тонны?

Решение:

Обозначим $S=2000$ кг - начальная масса бананов,
$X=250$ кг - массам бананов, продаваемых ежедневно,
$k=1-0,1=0,9$ - коэффициент, показывающий, во сколько раз уменьшается количество бананов после выкидывания испорченных,
$n$ - число полных дней.
Запишем, сколько бананов остается в конце каждого дня у Валентины Петровны:
1 день (2 ноября): $S_1=Sk-X$
2день (3 ноября): $S_2=(Sk-X)k-X=SK^2-X(k+1)$
Математическая модель похожа на ту, которую мы используем в задачах на кредиты с аннуитетными платежами. Только в нашем случае $k<1$ .
…
$n$ день ( $(n+1)$ ноября): $S_n=(((Sk-X)k-X)k-X)k-y=0$ .
В нашем уравнении $y$ – это масса бананов, которые Валентина Петровна продает в последний день, $y\leqslant X$ , потому что в последний день Валентина Петровна может продать не 250 кг бананов, а меньше. Сколько осталось, столько и продаст.
Тогда
$S_n=(((Sk-X)k-X)k-X)k=y$ ,

$y\leqslant X$ , поэтому $S_n=(((Sk-X)k-X)k-X)k\leqslant X$ ,

$(((Sk-X)k-X)k-X)k-X \leqslant 0.$

Раскрыв скобки и приведя подобные, получим:

$Sk^n-X(k^{n-1}+k^{n-2}+...+k^2+k+1) \leqslant 0$

Сумма в скобках $k^{n-1}+k^{n-2}+...+k^2+k+1$ - этосумма геометрической прогрессии, в которой $b_1=1$ , $q=k$ . Применим формулу суммы геометрической прогрессии:

$k^{n-1}+k^{n-2}+...+k^2+k+1=\frac{1-k^n}{1-k}$ . Тогда

$Sk^n-X\cdot \frac{1-k^n}{1-k}\leqslant 0$ ;

По условию, $k=0,9$ . Тогда $1-k=0,1$ .

$Sk^n-10X+10Xk^n\leqslant 0$

$k^n\leqslant \frac{10X}{S+10X}$ ; $k^n\leqslant \frac{2500}{4500}$ ;

$k^n\leqslant \frac{25}{45}$ ; $k^n\leqslant \frac{5}{9}\approx 0,56$ .

$k=0,9$ .
$0,9^2=0,81>0,56$ - не подходит

$0,9^4=0,6561>0,56$ - не подходит

$0,9^5=0,59049>0,56$ - не подходит

$0,9^6=0,531441<0,56$ - подходит.

Ответ: 6 дней

16. Анна Малкова

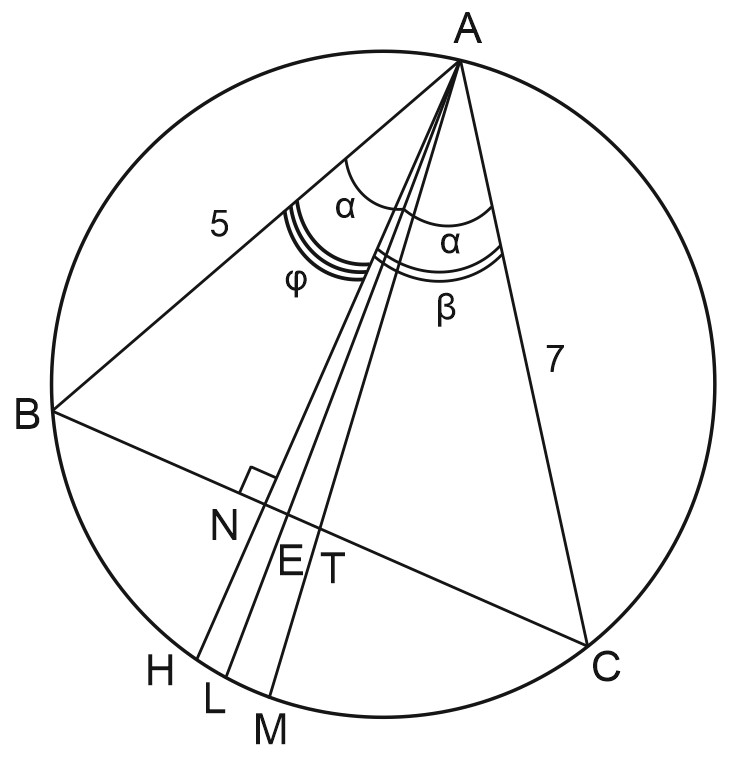
Остроугольный треугольник $ABC$ , в котором угол $A$ равен 60 градусам, вписан в окружность. Известны длины сторон треугольника: $AB = 5$ , $AC = 7$ . Биссектриса $AE$ треугольника $ABC$ пересекает описанную окружность в точке $L$ . Медиана треугольника $ABC$ , проведенная к стороне $BC$ , пересекает эту окружность в точке $M$ , а его высота, проведенная к $BC$ , пересекает ту же окружность в точке $H$ .
а) Докажите, что точка $L$ лежит между точками $H$ и $M$ .
б) Найдите $AE\cdot EL$ .

Решение:
а) Пусть $AN$ – высота треугольника, $AT$ – его медиана. Для того, чтобы показать, что точка $L$ лежит между точками $M$ и $H$ , достаточно показать, что точка $E$ лежит между точками $N$ и $T$ .

$\angle A=60$ °; $AE$ – биссектриса, отсюда $\angle BAE=\angle CAE=30$ °= $\alpha$ .

По свойству биссектрисы треугольника $BE:EC=AB:AC=5:7$ .

$T$ - середина $BC$ , тогда $BT=TC$ ⇒ $BE<BT$ .

Отсюда следует, что $\angle BAE<\angle BAT$ ;

Получили, что $\angle BAL<\angle BAM$ , значит, дуга $BL$ меньше дуги $BM$ .
Рассмотрим $\triangle ABN$ и $\triangle ACN$

Пусть $\angle BAN$ = $\varphi$ ⇒ $\angle CAN=$ $\beta=60^{\circ}-\varphi$ .

Из $\triangle BAN$ : $cos\varphi =\frac{AN}{AB}$

Из $\triangle CAN$ : $cos\beta =\frac{AN}{AC}$

$AB < AC$ по условию ⇒ $cos \varphi >cos \beta$ .

$\varphi+\beta=60$ °, значит, углы $\varphi$ и $\beta$ – острые,
Для острых углов $cos\varphi >cos\beta$ ⇔ $\varphi < \beta$ .

$\varphi < 60$ ° $-\varphi$ ;

$2\varphi<60$ °⇒ $\varphi<30$ °;

Отсюда $\varphi<\alpha$ и дуга $BH$ меньше дуги $BL$ .

Значит, $BH<BL<BM$ .

Мы доказали, что $L$ лежит между $H$ и $M$ .

б) Найдём $AE\cdot EL$

По теореме о пересекающихся хордах,
$AE\cdot EL=BE\cdot EC$

Из $\triangle ABC$ найдём $BC$ по теореме косинусов:

$BC^2=AB^2+AC^2-2AB\cdot AC\cdot cos\angle A$

$BC^2=5^2+7^2-2\cdot 5\cdot 7\cdot cos 60^{\circ}$

$BC^2=25+49-35=39$

$BC=\sqrt{39}$

По свойству биссектрисы угла треугольника: $BE:EC=AB:AC=5:7$ ,

$BE=\frac{5}{12}BC=\frac{5}{12}\sqrt{39}$ ;

$EC=\frac{7}{12}BC=\frac{7}{12}\sqrt{39}$ ;

$BE\cdot EC=\frac{5\cdot 7\cdot 39}{12\cdot 12}=\frac{35\cdot 13}{12\cdot 4}=\frac{455}{48}$ .

Ответ: $\frac{455}{48}$

17. Найдите все значения параметра $a$ , при каждом из которых система

$\left\{\begin{matrix}y(y+1)\leqslant 0 \\3x^2+3y^2-6a(x+y)+5a^2-6x+4a+3=0 \end{matrix}\right.$

имеет единственное решение.

Решение:

$\left\{\begin{matrix}y(y+1)\leqslant 0 \\3x^2+3y^2-6a(x+y)+5a^2-6x+4a+3=0 \end{matrix}\right.$

Решим систему графически в координатах $(x;y)$ .

Первое неравенство:
$y(y+1)\leqslant 0$ ⇔ $-1\leqslant y\leqslant 0$ .

Первое неравенство задает на плоскости горизонтальную полосу между прямыми $y=-1$ и $y=0$ вместе с границами полосы.

Во втором уравнении выделим полные квадраты.

$3x^2+3y^2-6a(x+y)+5a^2-6x+4a+3=0$ ;

$3x^2+3y^2-6ax-6ay+5a^2-6x+4a+3=0$ ;

$(3x^2-6ax+3a^2)+(3y^2-6ay+3a^2)+(-6x+6a)-a^2-2a+3=0$ .

Вынесем общий множитель за скобки и свернем по формулам сокращенного умножения.

$3(x-a)^2+3(y-a)^2-6(x-a)-a^2-2a+3=0$ .

Чтобы преобразования были проще, можно сделать замену $(x-a)=b$ .

Тогда $3(x-a)^2-6(x-a)+3=3b^2-6b+3=3(b^2-2b+1)=3(b-1)^2=3(x-a-1)^2$ .

Уравнение примет вид:

$3(x-a-1)^2+3(y-a)^2=a^2+2a$ .

Разделив обе части уравнения на 3, получим уравнение:

$(x-a-1)^2+(y-a)^2=\frac{a^2+2a}{3}$

При $a^2+2a>0$ это уравнение задает окружность с центром в точке $(a+1;a)$ и радиусом $R=\sqrt{\frac{a^2+2a}{3}}$ .

Координаты центра каждой окружности: $x=a+1$ ; $y=a$ .

Другими словами, $y=x-1$ - линия центров окружностей.

Так как координаты центра записаны с использованием параметра, то графиком второго уравнения является множество окружностей, двигающихся вдоль прямой $y=x-1$ .

Это происходит, когда $a^2+2a>0$ ⇔ $a(a+2)>0$ ⇔ $\left[\begin{array}{ccc}a>0\\a<-2\end{array}\right.$

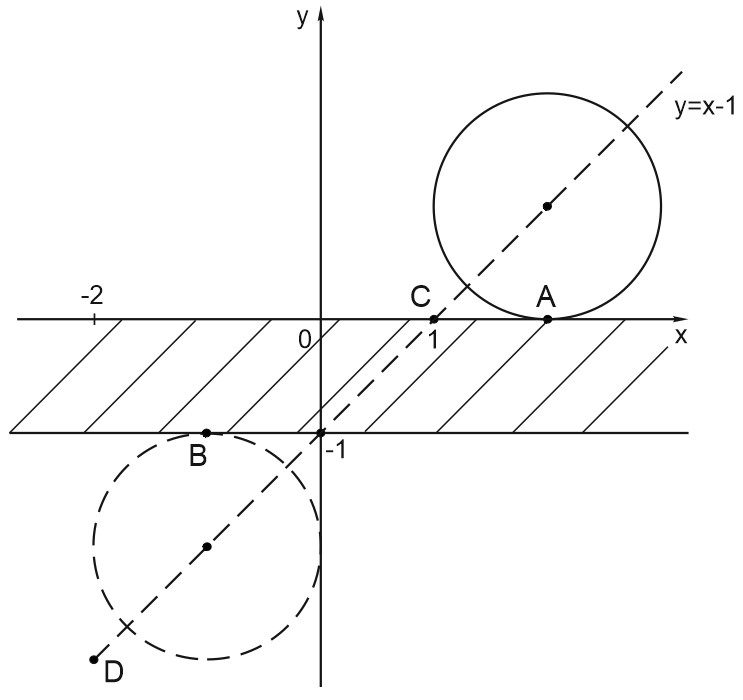
При $a^2+2a=0$ уравнение задает точку с координатами $x=a+1$ ; $y=a$ .

Это происходит, если $a=0$ или $a=-2$ .

При $a^2+2a<0$ – нет решений.

Система имеет единственное решение в следующих случаях:
1) Если окружность касается сверху прямой $y=0$ в точке $A$ или снизу касается прямой $y=-1$ в точке $B$ .

2) Второе уравнение системы задает точку, лежащую в полосе $-1 \leqslant y \leqslant 0$ .
В случае касания в точке $A$ расстояние от центра окружности до оси $X$ равно радиусу окружности.

$\left\{\begin{matrix}a>0 \\a^2=\frac{a^2+2a}{3}\end{matrix}\right.$
$\left\{\begin{matrix}a>0 \\3a^2=a^2+2a\end{matrix}\right.$
$\left\{\begin{matrix}a>0 \\2a^2-2a=0\end{matrix}\right.$

$\left\{\begin{matrix}a>0 \\\left[\begin{array}{ccc}a=0\\a=1\end{array}\right.\end{matrix}\right.$

$a=1$

В случае касания в точке $B$ :

$\left\{\begin{matrix}a < -2 \\(a+1)^2=\frac{a^2+2a}{3}\end{matrix}\right.$
$\left\{\begin{matrix}a < -2 \\3a^2+6a+3=a^2+2a\end{matrix}\right.$
$\left\{\begin{matrix}a < -2 \\2a^2+4a+3=0\end{matrix}\right.$

решений нет, так как дискриминант квадратного уравнения отрицателен. Значит, касания в точке $B$ не может быть.

Система также имеет единственное решение, если окружность превращается в точку и при этом лежит внутри полосы, заданной первым неравенством. Мы сказали, что это происходит при $a=0$ или $a=-2$ .
Если $a=0$ , получим точку $C(1;0)$ . Она лежит на границе полосы, заданной первым неравенством.
Если $a=-2$ , получим точку $D(-1;-2)$ . Она не принадлежит полосе.
Получили $a=1$ и $a=0$ .

Ответ: $a\in$ {0;1}

18. Полина записала несколько различных натуральных чисел, все цифры которых нечетны, после чего нашла сумму этих чисел и обозначила ее через S.
а) Может ли сумма цифр числа S быть нечетным числом, если Полина записала ровно четыре числа?
б) Может ли произведение цифр числа S быть нечетным числом, если S > 1000?
в) Пусть десятичная запись числа S состоит из 2021 цифры. Какое наименьшее натуральное значение может принимать произведение цифр числа S?

Решение:

а) Да, может, например, если записать числа 1, 3, 5 и 7, их сумма $S=16$ , сумма цифр этого числа нечетна.

Другой пример: 3, 7, 9, 11, сумма 30, сумма цифр нечетна

б) Да, может, например, если записать числа 13, 99 и 999, их сумма $s=1111$ , произведение цифр этого числа нечетно.
в) Рассмотрим числа вида 9, 99, 999, ..., 999...9 (в последнем числе 2020 девяток). Их сумма равна:
9 + 99 + 999 + ... + 999...9 = 10 + 100 + 1000 + ... + 100...0 – 2020 = 1111...0 – 2020 = 111...1 − 2021.
Так как
2021 = 1999 + 22 = 1999 + 19 + 3,
то
1111...1 = 3 + 19 + 1999 + 9 + 99 + 999 + ... + 999...9.
Произведение полученного цифр 2021-значного числа равно единице, очевидно, это наименьшее натуральное значение.

Ответ:
а) да,
б) да,
в) 1.

Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «ЕГЭ-2023 Вариант 3, решения» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 25.09.2023

ЕГЭ-2023 Вариант 3, решения

Это полезно