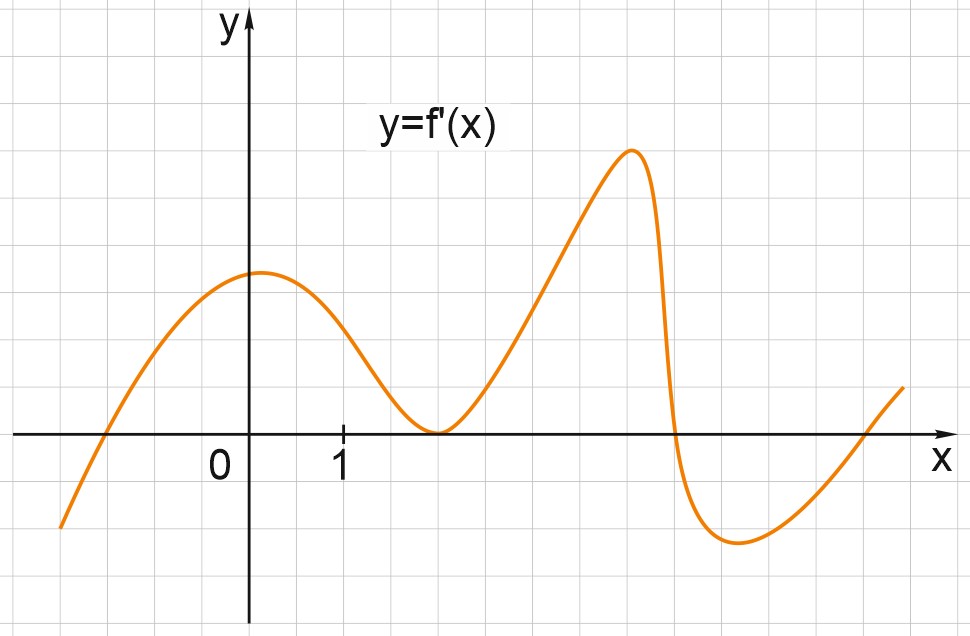Видеоразбор: https://www.youtube.com/watch?v=QUMfQwd_Rr0&t;t\&t=439s
и https://www.youtube.com/watch?v=tqjQ5SpT8rc;t\&t=1s
Часть 1. Задания с кратким ответом
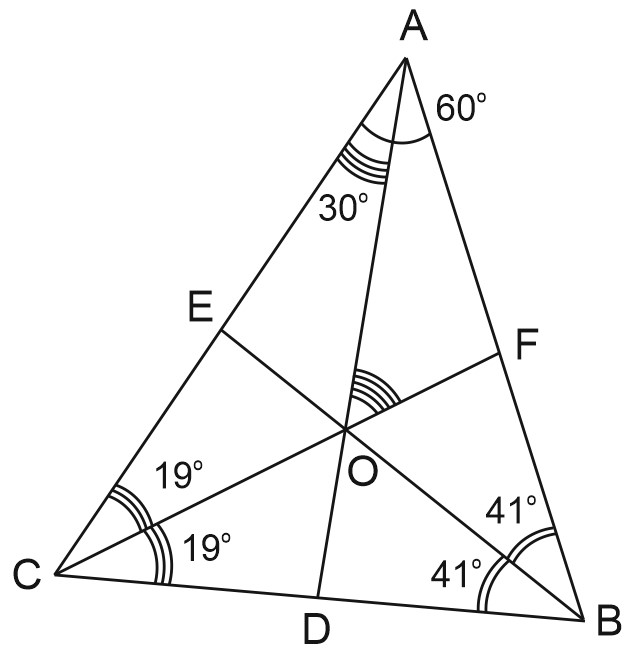
1. В треугольнике \(ABC\) угол \(A\) равен \(60^{\circ}\), угол \(B\) равен \(82^{\circ}\). \(AD\), \(BE\) и \(CF\) — биссектрисы, пересекающиеся в точке \(O\). Найдите угол \(AOF\). Ответ дайте в градусах.
Решение:
\(\angle A=60\); \(\angle B=82\); ⇒ \(\angle C=180^{\circ}-(60^{\circ}+82^{\circ})=38^{\circ}\)
\(AD\) - биссектриса \(\angle CAB\)⇒\(\angle CAD=30^{\circ}\)
\(CF\) - биссектриса \(\angle ACB=38^{\circ}\)⇒\(\angle ACF=19^{\circ}\)
\(\angle AOF\) – внешний угол треугольника \(ACO\). Он равен сумме внутренних углов этого треугольника, не смежных с ним.
\(\angle AOF=\angle ACO+\angle CAO=19+30=49^{\circ}.\)
Ответ: 49
2. Даны векторы \( \overrightarrow{a}=(3; 1)\), \( \overrightarrow{b}=(2;-3)\) и \( \overrightarrow{c}=(-2; 1)\). Найдите значение выражения \((\overrightarrow{a}-\overrightarrow{b})\cdot\overrightarrow{c}\).
Решение:
\(\overrightarrow{a}=(3; 1)\)
\(\overrightarrow{b}=(2; -3)\)
\(\overrightarrow{c}=(-2; 1)\)
Найдем \((\overrightarrow{a}-\overrightarrow{b})\cdot\overrightarrow{c}\).
\(\overrightarrow{m}=\overrightarrow{a}-\overrightarrow{b}=(3-2;1+3)=(1;4)\)
\(\overrightarrow{m}\cdot\overrightarrow{c}=x_m x_c+y_m y_c=1\cdot(-2)+4\cdot1=-2+4=2\).
Ответ: 2.
2. Анна Малкова
Диаметр апельсина равен 10 см. Диаметр апельсина без кожуры равен 8 см. Сколько процентов от объема апельсина занимает кожура? Апельсин (в кожуре и без нее) считать шарообразным.
Решение:
Пусть \(D_1=10\) см – диаметр апельсина с кожурой, \(D_2 = 8\) см – диаметр апельсина без кожуры.
Пусть \(V_1\) – объем апельсина с кожурой, \(V_2\) – объем апельсина без кожуры. Тогда кожура апельсина занимает объем, равный \(V_1 - V_2\). Найдем отношение объема кожуры к объему всего апельсина и умножим на 100%. Это и будет ответ на вопрос задачи.
Формула объема шара: \(V=\frac{4}{3}\pi R^3\)
\(\frac{V_1-V_2}{V_1}\cdot 100\)%\(=\frac{\frac{4}{3} \pi R_1^3-\frac{4}{3}\pi R_2^3}{\frac{4}{3}\pi R_1^3}=\)\(\frac{R_1^3-R_2^3}{R_1^3}=\frac{D_1^3-D_2^3}{D_1^3}=\frac{10^3-8^3}{10^3}=\)\(\frac{(10-8)(10^2+8\cdot 10+8^2)}{1000}=\frac{2\cdot 244}{1000}=48,8\)%
Мы получили, что объем кожуры равен почти половине объема апельсина!
Ответ: 48,8
3. Александра Антонова
В шкафу Деда Мороза вперемешку лежат все его 9 шапок, а также случайно оказавшаяся там шапочка Снегурочки. 31 декабря Дед Мороз, опаздывая на детский утренник, наугад надевает первую попавшуюся шапку. Найдите вероятность того, что он возьмет не свою шапку.
Решение:
Cогласно определению вероятности, она равна отношению числа благоприятных исходов к общему число исходов. Благоприятный исход один из десяти возможных, значит, \(p=0,1\).
Ответ: 0,1
4. Анна Малкова
Студент Василий заметил, что если он в новогоднюю ночь загадывает желание, то оно сбывается с вероятностью 0,4. Маша сказала, что у неезагаданные в новогоднюю ночь желания сбываются с вероятностью 0,8.
Маша и Василий договорились в новогоднюю ночь загадать по 7 желаний.
Во сколько раз вероятность того, что у Маши исполнится ровно 6 желаний, больше вероятности того, что у Василия исполнится ровно 5 желаний? Ответ округлите до сотых.
Решение:
Это задача на формулу Бернулли.
Найдем вероятности:
\( P_M \) – вероятность того, что у Маши исполнится ровно 6 желаний из 7,
\( P_B \) – вероятность того, что у Василия исполнится ровно 5 желаний из 7.
\(P_M=C_7^6\cdot (\frac{8}{10})^6\cdot \frac{2}{10}\)
\(P_B=C_7^5\cdot (\frac{4}{10})^5\cdot (\frac{6}{10})^2\)
\(\frac{P_M}{P_B}=\)\(\frac{C_7^6\cdot 8^6\cdot 2}{C_7^5\cdot 4^5\cdot 6^2}=\frac{\not 7!\cdot 2^{18}\cdot 2\cdot 5!\cdot 2!}{6!\cdot \not 7!\cdot 2^{10}\cdot 2^2\cdot 3^2}=\)\(\frac{2^{10}\cdot \not 5\cdot \not 4\cdot \not 3\cdot \not 2\cdot \not 1}{6\cdot \not 5\cdot \not 4\cdot \not 3\cdot \not 2\cdot \not 1 \cdot 2^2\cdot 3^2}=\frac{2^8}{6\cdot 3^2}=\frac{2^8}{2\cdot 3^3}=\frac{2^7}{3^3}=\frac{128}{27}\approx 4,74\)
Ответ: 4,74
5. Решите уравнение: \(|x^2-2x|=|x+4|\). Если корней несколько, в ответе запишите их сумму.
Решение:
Так как обе части уравнения неотрицательны, их можно возвести в квадрат. Получим:
\((x^2-2x)^2=(x+4)^2\)
Перенесем все в левую часть уравнения и воспользуемся формулой разности квадратов
\((x^2-2x)^2-(x+4)^2=0\)
\((x^2-2x-x-4)(x^2-2x+x+4)=0\)
\((x^2-3x-4)(x^2-x+4)=0\)
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Получим совокупность:
\(\left[\begin{array}{ccc}
x^2-3x-4=0 \\
x^2-x+4=0\end{array}\right.\)
Решили отдельно каждое уравнение:
\(x^2-3x-4=0\)⇔\(\left[\begin{array}{ccc}
x=4 \\
x=-1\end{array}\right.\)
\(x^2-x+4=0\); \(D=1-16=-15<0\); корней нет. Сумма корней: \(4-1=3\). Ответ: 3 6. Вычислите: \(lg(\frac{8\cdot 100^{2,4}}{2^{5,8}\cdot 5^{2,8}})\). Решение: 1) Упростим дробь под логарифмом: \(\frac{8\cdot 100^{2,4}}{2^{5,8}\cdot 5^{2,8}}=\frac{2^3\cdot (2^2\cdot 5^2)^{2,4}}{2^{5,8}\cdot 5^{2,8}}=\frac{2^3\cdot 2^{4,8}\cdot 5^{4,8}}{2^{5,8}\cdot 5^{2,8}}=\frac{2^3\cdot 5^2}{2}=2^2\cdot 5^2=10^2\) 2) \(lg(\frac{8\cdot 100^{2,4}}{2^{5,8}\cdot 5^{2,8}})=lg 10^2=2\) Ответ: 2 7. Анна Малкова
На рисунке изображен график \(y=f'(x)\) - производной функции \(y=f(x)\). В какой точке отрезка [1;5] функция \(y=f(x)\) принимает наибольшее значение?
Решение:
На рисунке изображен график \(y=f'(x)\).
На отрезке [1;4,5] производная неотрицательна. Это значит, что функция \(y=f(x)\) на интервалах [1; 2) и (2; 4,5] монотонно возрастает.
Заметим, что в точке \(x=2\) производная равна нулю, но не меняет знак.
Для функции \(y=f(x)\) точка \(x=2\) – это точка перегиба.
На интервале (4,5; 5] производная отрицательна, функция на этом интервале убывает.
Значит, \(x=4,5\) – точка максимума функции.
В ней производная равна нулю и меняет знак с «+» на «-».
Поэтому при \(x=4,5\) функция принимает наибольшее значение на отрезке [1;5].
Ответ: 4,5
8. Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела \(P\), измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвертой степени температуры: \(P=\sigma ST^4\), где \(\sigma =5,7\cdot 10^{-8}\) — постоянная, площадь \(S\) измеряется в квадратных метрах, а температура \(T\) — в градусах Кельвина. Известно, что некоторая звезда имеет площадь \(S=\frac{1}{16}\cdot 10^{20}\) м², а излучаемая ею мощность \(P\) не менее \(9,12\cdot 10^{25}\) Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
Решение:
\(\sigma =5,7\cdot 10^{-8}\); \(P=\sigma ST^4\)
\(S=\frac{1}{16}\cdot 10^{20}\)
\(P\geqslant 9,12\cdot 10^{25}\)
Подставим данные и получим неравенство:
\(5,7\cdot10^{-8}\cdot \frac{1}{16}\cdot 10^{20}\cdot T^4\geqslant 9,12\cdot 10^{25}\)
\(5,7\cdot \frac{1}{16}\cdot 10^{12}\cdot T^4\geqslant 9,12\cdot 10^{25}\)
\(T^4\geqslant \frac{9,12\cdot 10^{25}\cdot 16}{5,7\cdot 10^{12}}=\frac{30,4\cdot 16\cdot 10^{13}}{19}=16\cdot 16\cdot 10^{12}=(4\cdot 10^3)^4\)
\(T\geqslant 4000\)
\(T_{min}=4000\) К. Из физики мы знаем, что температура в Кельвинах может быть только положительной.
Ответ: 4000
9. Анна Малкова
В ожидании Нового Года Дед-Мороз и Санта Клаус затеяли гонки по круговой орбите вокруг Земли. Длина окружности, по которой они летают, составляет 33 тыс. км.
Первым стартует (на оленях) Санта Клаус. Через 30 часов из той же точки следом за ним вылетает (на тройке лошадей) Дед-Мороз. Через 10 часов после старта он в первый раз догоняет Санта Клауса, а еще через 44 часа догоняет во второй раз. Найдите скорость Деда Мороза. Ответ выразите в км/ч.
Решение:
Пусть скорость Санта Клауса равна \(x\) км/ч, а скорость Деда Мороза \(y\) км/ч.
Составим уравнение для момента встречи.
Дед Мороз был в пути 10 часов и пролетел то же расстояние, что и Санта Клаус за 40 часов.
\(10y=40x\) и
\(y=4x\)
Через 44 часа Дед Мороз снова догнал Санта Клауса. Это значит, что расстояние, которое за это время преодолел Дед Мороз, на 1 круг, то есть на 33 тысячи километров больше расстояния, которое пролетел Санта.
\(44y-44x=33000\)
\(4y-4x=3000\)
\(4\cdot 4x-4x=3000\)
\(12x=3000\)
\(x=250\) км/ч – скорость Санта Клауса, \(250\cdot 4=1000\) км/ч –скорость Деда мороза
Ответ: 1000
10. Анна Малкова
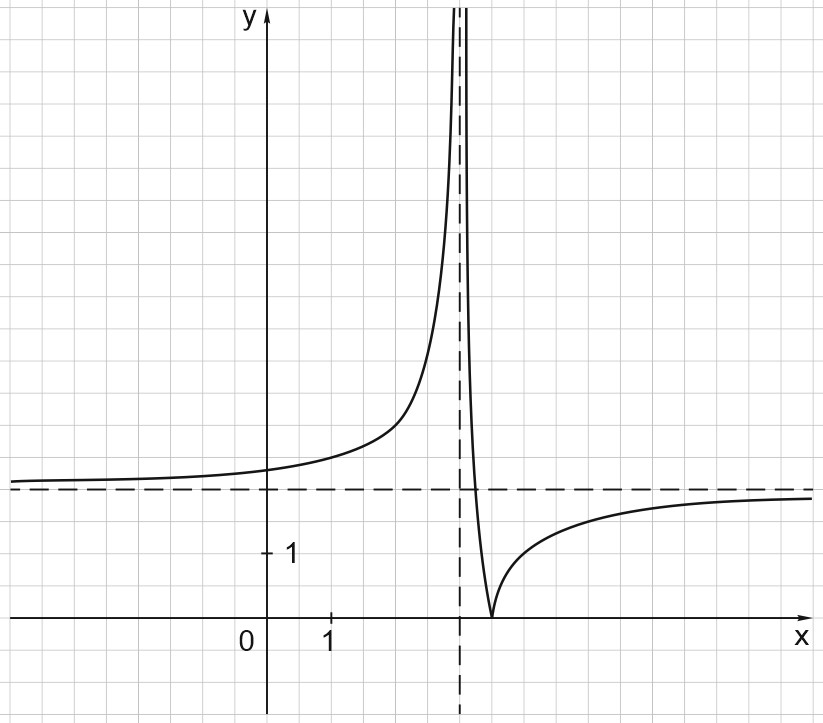
На рисунке изображен график функции \(y=|\frac{a-cx+bc}{x-b}|\), где \(a, b, c\) - целые, \(a>0\).
Найдите \(y(28)\).
Решение:
На рисунке график функции \(y=|\frac{a}{x-b}-c|=|\frac{-1}{x-3}+2|=|\frac{1}{x-3}-2|\);
\(y(28)=|\frac{1}{25}-2|=2-0,04=1,96\)
Ответ: 1,96
11. Анна Малкова
Найдите наибольшее значение функции \(y=8-16 sin^2 \frac{x}{3}\) на отрезке \( [\frac{\pi}{2};\pi]. \)
Решение:
\(y=8-16 sin^2 \frac{x}{3}=8(1-2sin^2 \frac{x}{3})=8cos\frac{2x}{3}\)
(применили формулу косинуса двойного угла).
Сделаем замену переменной: \(t=\frac{2x}{3}\).
Тогда \( y=8 cos t\).
Если \( x\in [\frac{\pi}{2};\pi] \), то \( t \in [\frac{\pi}{3};\frac{2 \pi}{3}]\).
Найдём наибольшее значение функции \( y=8 cos t\) при \(t\in [\frac{\pi}{3};\frac{2 \pi}{3}]\).
Функция \( y=cos t\) монотонно убывает при \(t\in [0;\pi]\).
Это значит, что наибольшее значение функции \( y=8 cos t\) на отрезке \([\frac{\pi}{3};\frac{2 \pi}{3}]\) достигается в левом конце этого отрезка: \(y_{max}=y(\frac{\pi}{3})=8\cdot \frac{1}{2}=4\).
Ответ: 4
Часть 2. Задания с развернутым ответом
12. Анна Малкова
а) Решите уравнение: \(\frac{2+cos 2x-3cos x}{\sqrt{9-25 cos^2 x}}=0\)
б) Найдите все корни уравнения на отрезке \([-\frac{3 \pi}{2};\frac{\pi}{3}].\)
Решение:
Уравнение равносильно системе:
\(\left\{\begin{matrix}
2+cos 2x-3 cos x=0 \\
9-25 cos^2 x>0\end{matrix}\right.\)
Решим первое уравнение системы. Применим формулу косинуса двойного угла.
\(2+2cos^2 x-1-3 cos x=0\)
Сделаем замену: \(cos x=t\), \(|t|\leqslant 1\)
\(2t^2-3t+1=0\); \(D=1\); \(t=\frac{3\pm 1}{4}\); \(t_1=1\); \(t_2=\frac{1}{2}\)
Получим:
\(\left\{\begin{matrix}
\left[\begin{array}{ccc}
t=1 \\
t=\frac{1}{2}\end{array}\right.\\
t^2<\frac{9}{25}\end{matrix}\right.\) \(\Leftrightarrow \)\(t=\frac{1}{2}\); \(cox x=\frac {1}{2}\); \(x=\pm \frac{\pi}{3}+2\pi n\), \(n\in Z\)
б) Найдем корни на отрезке \([-\frac{3\pi}{2};\frac{\pi}{3}]\).
Отметим на единичной окружности отрезок \([-\frac{3\pi}{2};\frac{\pi}{3}]\) и найденные серии решений.
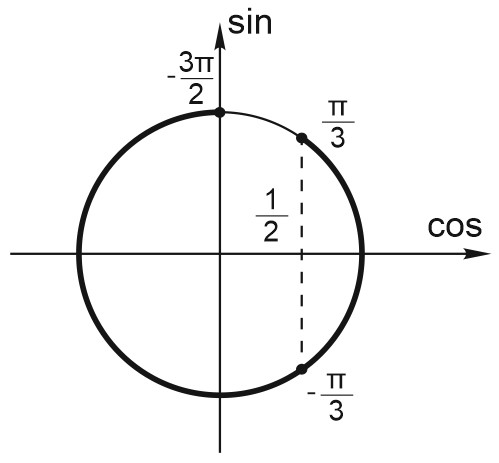
Видим, что указанному отрезку принадлежат точки: \(-\frac {\pi}{3}; \frac {\pi}{3}\).
Ответ: а) \(x=\pm \frac{\pi}{3}+2\pi n\), \(n\in Z\);
б) \(-\frac {\pi}{3}; \frac {\pi}{3}\).
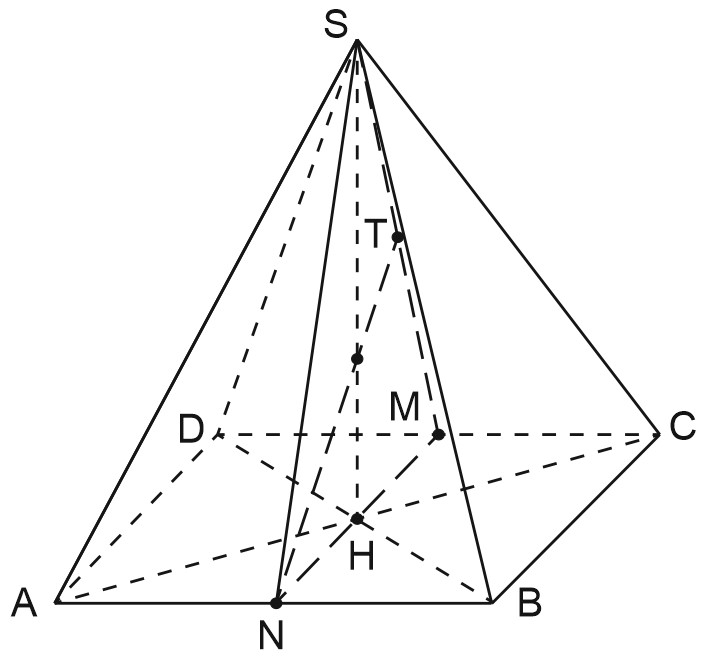
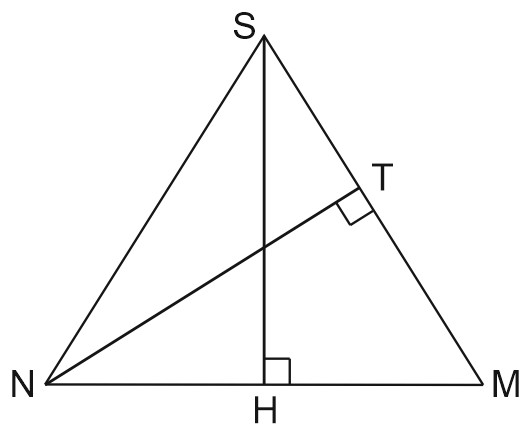
13. В правильной четырёхугольной пирамиде \(SABCD\) боковое ребро \(SA\) равно \(\sqrt{5}\), а высота \(SH\) пирамиды равна \(\sqrt{3}\). Точки \(M\) и \(N\) — середины рёбер \(CD\) и \(AB\) соответственно, \(NT\) — перпендикуляр из точки \(N\) на плоскость \(SCD\).
а) Докажите, что точка \(T\) является серединой \(SM\).
б) Найдите расстояние между прямыми \(NT\) и \(SC\).
Решение:
а) Построим \(NT\) и докажем, что точка \(T\) – середина отрезка \(SM\).
Рассмотрим сечение пирамиды \(SABCD\) плоскостью \(SMN\).
В треугольнике \(SMN\) проведем высоту \(NT\).
Заметим, что \(MN\perp DC\), \(SM\perp DC\),и значит, \((SMN)\perp DC\).
Мы воспользовались признаком перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости
Тогда \(NT\perp DC\).
Действительно, если прямая \( DC \) перпендикулярна плоскости \( SMN \), то она по определению перпендикулярна любой прямой, лежащей в плоскости \( SMN \). В том числе и прямой \( NT \).
Кроме того, \( NT\perp SM \) по построению. Мы получили, что \( NT\perp(SDC) \).
Высота пирамиды \(SH=\sqrt{3}\),а боковое ребро \(SA=\sqrt{5}\). Из треугольника \(SAH\) найдем \(AH=\sqrt{2}\),и тогда \(AC=2\sqrt{2}\)
\(AB=AD=MN=2.\)
\(SN\) – апофема боковой грани пирамиды. Из треугольника \(SNA\) найдем
\(SN=2\), и тогда треугольник \(SNM\) – правильный, \(NT\) – его высота и медиана, \(T\) – середина \(SM\).
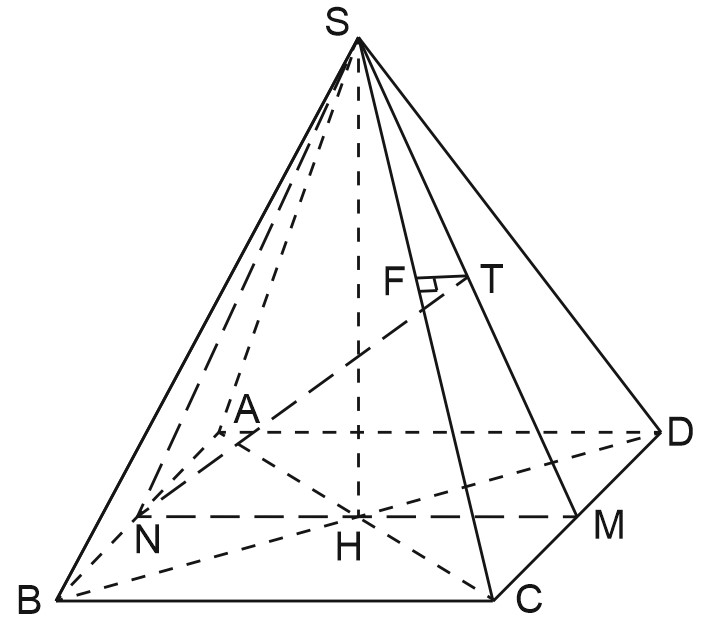
б) Найдем расстояние между \(NT\) и \(SC\).
Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.
\(NT\perp (SDC)\),изначит, \(NT\perp SC\).
Опустим из точки \(T\) в плоскости \(SDC\) перпендикуляр \(TF\) на ребро \(SC\). Обратите внимание – сделан новый чертеж, в другом ракурсе.
Получим, что \(TF\perp SC\) по построению, \(TF\perp NT\), поскольку \(TF\in (SDC)\), \((SDC)\perp NT\).
Треугольники \(STF\) и \(SCM\) подобны (по двум углам),
\(\frac{TF}{CM}=\frac{ST}{SC}\);
\(TF=CM\cdot \frac{ST}{SC}=1\cdot \frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}\).
Ответ: \(\frac{\sqrt{5}}{5}\)
14. Кирилл Буйлов
Решите неравенство: \(log_2((x+5)(x^2-7x+6))+log_2(\frac{9-x}{x^2-7x+6})\leqslant log_2 x+3\).
Решение:
Неравенство равносильно системе:
\(\left\{\begin{matrix}
(x+5)(x^2-7x+6)>0 \\
\frac{9-x}{x^2-7x+6}>0 \\
x>0 \\
(x+5)(9-x)\leqslant 8x\end{matrix}\right.\)
Мы записали в одну систему и ОДЗ, и преобразованное неравенство. Поскольку логарифмическая функция \(y=log_2\) монотонно возрастает, из неравенства \(log_2 t_1\leqslant log_2 t_2\) следует неравенство \(t_1\leqslant t_2\) (при \(t_1>0\), \(t_2>0\)).
\(\left\{\begin{matrix}
x>0 \\
x^2-7x+6>0 \\
9-x>0 \\
9x+45-x^2-5x-8x\leqslant 0\end{matrix}\right.\)
\(\left\{\begin{matrix}
x>0 \\
(x-1)(x-6)>0 \\
x<9 \\
-x^2-4x+45\leqslant 0\end{matrix}\right.\)
\(\left\{\begin{matrix}
x>0 \\
(x-1)(x-6)>0 \\
x<9 \\
x^2+4x-45\geqslant 0\end{matrix}\right.\)
\(\left\{\begin{matrix}
x>0 \\
(x-1)(x-6)>0 \\
x<9 \\
(x+9)(x-5)\geqslant 0\end{matrix}\right.\)
Отметим на числовой прямой решения системы:

Запишем ответ:
Ответ: (6;9)
15. Анна Малкова
1 сентября 2019 года в заповеднике обитало 256 криворогих оленей. Известно, что в течение года численность популяции криворогих оленей увеличивается в среднем на 25% (за счет естественного прироста). Кроме того, биологи собираются до 2 сентября 2023 года увеличить количество оленей в заповеднике не менее чем до 1000 и для этого 1 сентября 2020, 2021, 2022 и 2023 года будут завозить в заповедник одинаковое количество новых оленей. Какое наименьшее количество оленей им придется завозить в заповедник ежегодно?
Решение:
Пусть \(S=256\) – начальное количество оленей, \(k=1,25=\frac{5}{4}\); \(x\) оленей завозят ежегодно.
\((((Sk+x)\cdot k+x)\cdot k+x)\cdot k+x\geqslant 1000\);
\(Sk^4+x(k^3+k^2+k+1)\geqslant 1000\);
\(256\cdot (\frac{5}{4})^4=\frac{256}{16^2}\cdot 25^2=625\);
\(625+x(k^2+1)(k+1)\geqslant 1000\);
\(x(\frac{5}{4}+1)(\frac{25}{16}+1)\geqslant 375\);
\(\frac{41}{16}x\geqslant\frac{125\cdot 4}{3}\);
\(x\geqslant\frac{125\cdot 64}{123}\);
\(x\geqslant \frac{125}{123}\cdot 64\);
\(x\geqslant 65\).
Как решить без калькулятора.
Очевидно, \(x>64\). Проверим \(x=65\).
\(\frac{65}{64}\vee \frac{125}{123}\)
\(1+\frac{1}{64}\vee 1+ \frac{2}{123}\)
\(\frac{1}{64}\vee \frac{2}{123}\)
\(\frac{2}{128}< \frac{2}{123}\) Если \(x=66\), \(\frac{66}{64}\vee \frac{125}{123}\) \(\frac{2}{64}\vee \frac{2}{123}\) \(\frac{2}{64}> \frac{2}{123}\)
\(x=66\) – подходит.
Ответ: 66.
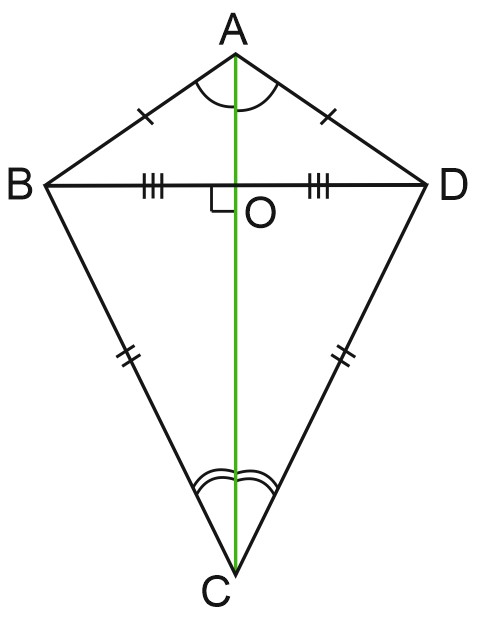
16. В четырехугольнике \(ABCD\) противоположные стороны не параллельны. Диагонали четырехугольника \(ABCD\) пересекаются в точке \(O\) под прямым углом и образуют 4 подобных треугольника, у каждого из которых одна из вершин – точка \(O\).
а) Докажите, что вокруг четырехугольника \(ABCD\) можно описать окружность
б) Найдите радиус вписанной окружности, если \(AC = 10\), \(BD = 26\).
Решение:
Диагонали четырехугольника \(ABCD\) перпендикулярны, но параллельных сторон нет, значит, нам не подходят ромб и трапеция.
Диагонали четырехугольника \(ABCD\) пересекаются в точке \(O\) под прямым углом и образуют 4 подобных прямоугольных треугольника, у каждого из которых одна из вершин – точка \(O\).
Пусть острые углы этих подобных треугольников равны \(\alpha \) и \(\beta \).
Возможны такие случаи:
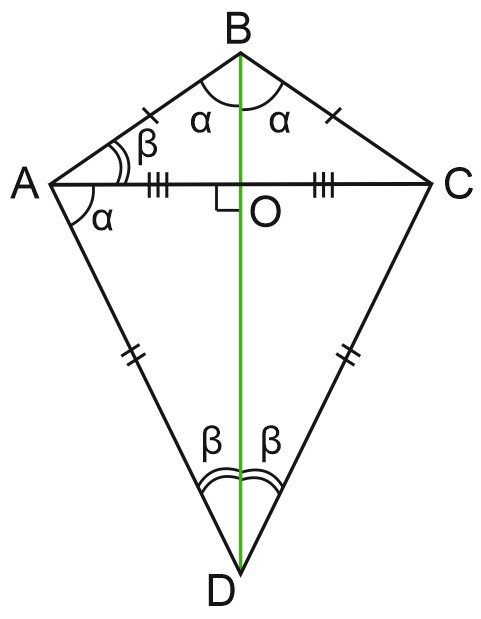
1) Диагональ ВD является биссектрисой углов \(B\) и \( D\) четырехугольника. Пусть угол \(B\) равен \(2\alpha \), а угол \(D\) равен \(2\beta \). Тогда оставшиеся углы \(A\) и \(C\) четырехугольника равны \(\alpha+\beta=90^{\circ}\).
Треугольники \(BAD\) и \(BCD\) равны по стороне и двум углам.
Отсюда \(AB = BC\), \(AD = CD\). Наш четырехугольник имеет две пары равных сторон, причем равные стороны – смежные. Такой четырехугольник называется дельтоид.
В нем \(\angle A+\angle C=90^{\circ}+90^{\circ}=180^{\circ}\), значит, четырехугольник \(ABCD\) можно вписать в окружность.
2) Если \(\angle A=\angle C=2\alpha\), то \(\angle B=\angle D=2\beta\), получается ромб, у него противоположные стороны параллельны, противоречие. Это нам не подходит.
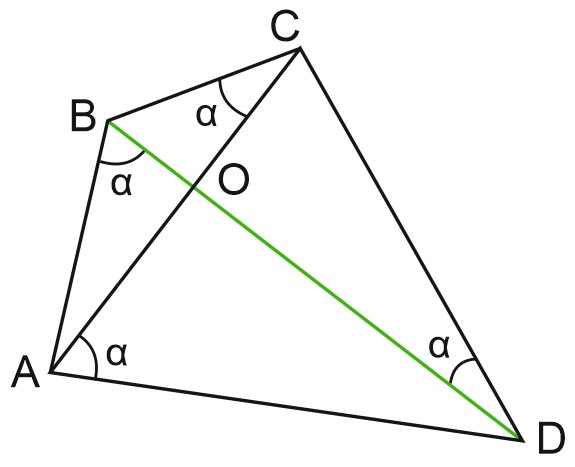
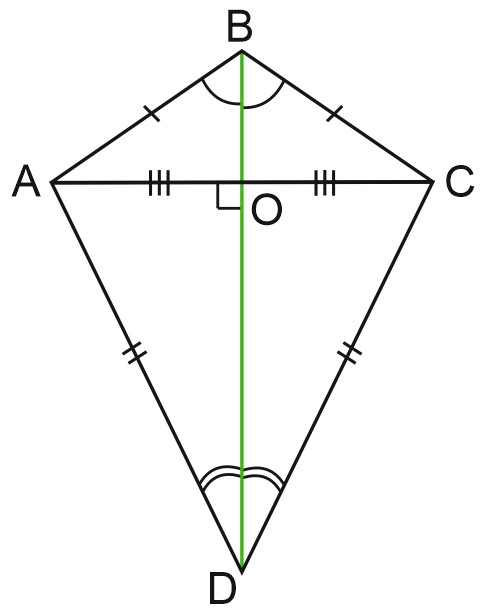
3) Рассмотрим такой случай:
Ни одна из диагоналей не является биссектрисой угла четырехугольника. Рассмотрим подобные прямоугольные треугольники \(AOB\), \(BOC\), \(COD\), \(AOD\).
В каждом из них выразим \(tg\alpha \) как отношение противолежащего катета к прилежащему.
\(tg\alpha =\frac{AO}{OB}=\frac{BO}{OC}=\frac{OC}{OD}=\frac{OD}{AO}\), отсюда
\(OB^2=AO\cdot OC\)
\(OD^2=OC\cdot AO\)
Значит, \(OB^2=OD^2\)⇒\(OB=OD\).
Аналогично, \(AO^2=OB\cdot OD\); \(OC^2=BO\cdot OD\), получили: \(AO=OC\).
Получили, что диагонали этого четырёхугольника в точке пересечения делятся пополам, и этот четырехугольник - параллелограмм, противоречие.
Остается только вариант (1), то есть дельтоид.
б) Найдём радиус вписанной окружности, если \(AC=10\); \(BD=26\). Четырехугольник \(ABCD\) вписан в окружность, и прямоугольный треугольник \(ABD\) также вписан в окружность, причем центр описанной окружности лежит на середине его гипотенузы \(BD\),
\(R=\frac{BD}{2}\).
По условию, \(AC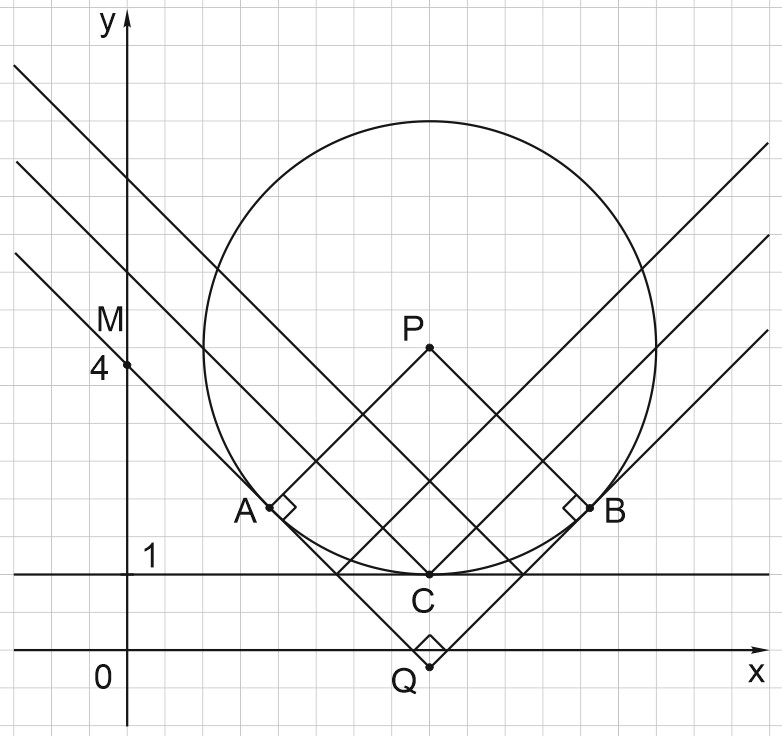
Система имеет ровно три различных решения, если график функции \(y=|x-a|+1\) ровно 3 раза пересекает окружность. Это происходит в следующих случаях:
1) Вершина графика \(y=|x-a|+1\) находится в точке \(C(4;1)\).
Тогда \(a=4\).
2) Левая ветвь графика функции \(y=|x-a|+1\) касается окружности в точке \(A\), а правая ветвь пересекает окружность в двух точках.
3) Левая ветвь графика функции \(y=|x-a|+1\) пересекает окружность в двух точках, а правая ветвькасается окружности в точке \(B\).
Найдём значение параметра в точках касания геометрическим способом.
Касательная перпендикулярна радиусу, проведённому в точку касания.
Угол \(AQB\) – прямой,так как левая и правая ветви графика функции \(y=|x-a|+1\) взаимно перпендикулярны. Так же, как и у графика функции \(y=|x|\), где правая и левая ветви - это биссектрисы первого и второго координатных углов. А биссектрисы смежных углов взаимно перпендикулярны.
Значит, радиус \(PA\) параллелен правой ветви графика \(y=|x-a|+1\),
Радиус \(PB\) параллелен левой ветви графика \(y=|x-a|+1\).
Получили:
\(AP\parallel QB\); \(BP\parallel AQ\); \(\angle AQB=\angle PAQ=\angle PBQ=90^{\circ}\), \(AP=BP\),⇒\(APBQ\) – квадрат.
Тогда \( PA=AQ=R=3 \) .
\( PQ \) – диагональ квадрата, \( PQ=3\sqrt{2}\). Заметим, что \(C\in PQ\).
Длина отрезка \(PQ\) равна \( y_P-y_Q \), отсюда \( y_Q=y_P-PQ=4-3\sqrt{2} \). Мы нашли ординату точки \(Q\).
\(Q(4; 4-3\sqrt{2})\).
Для прямой \(AQ\), на которой лежит левая ветвь графика модуля,
\(y=a-x+1\).Подставим координаты точки \(Q\):
\(4-3\sqrt{2}=a-4+1\)⇒\(a=7-3\sqrt{2}\).
В случае касания в точке \(A\): \(a=7-3\sqrt{2}\).
Для прямой \(BQ\), на которой лежит правая ветвь графика модуля,
\(y=x-a+1\). Подставим координаты точки \(Q\):
\(4-3\sqrt{2}=4-a+1\)⇒\(a=1+3\sqrt{2}\)
Для случая касания в точке \(B\): \(a=1+3\sqrt{2}\).
Получили, что система уравнений имеет ровно 3 различных решения, если
\(a=4\); \(a=1+3\sqrt{2}\); \(a=7-3\sqrt{2}\).
Во всех остальных случаях система имеет больше или меньше трех решений.
Ответ: 4; \(1+3\sqrt{2}\); \(7-3\sqrt{2}\).
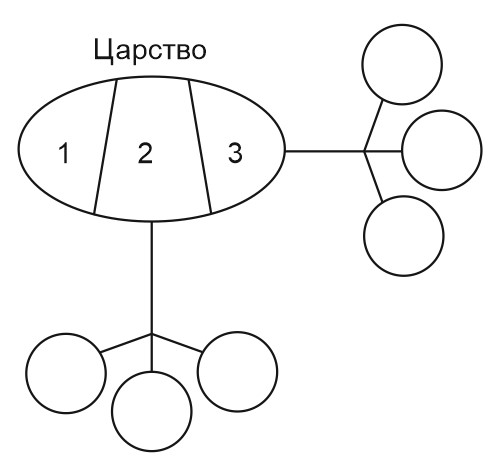
18. В некотором царстве было несколько (более двух) княжеств. Однажды некоторые из этих княжеств объявили себя царствами и разделились каждое на то же самое число княжеств, которое было в самом начале. Затем всё новые и новые княжества из числа прежних и вновь образующихся объявляли себя царствами и делились каждое на то же самое число княжеств, которое было в самом начале.
а) Могло ли сразу после одного из делений общее число княжеств стать равным 102?
б) Могло ли в какой‐то момент времени общее число княжеств стать равным 320, если известно, что сразу после одного из делений общее число княжеств было равно 162?
в) Сколько княжеств было в самом начале, если сразу после какого‐то из делений общее число княжеств стало ровно в 38 раз больше первоначального?
Решение:
Вначале было nкняжеств, \(n\geqslant 3\).
Например, пусть вначале царство состояло из трёх княжеств. И третье княжество решило выйти из царства. А выйдя, разделилось на три княжества.
Стало \(3-1+3=3+3-1\) княжеств. Вместо одного княжества стало три.
И пусть аналогичное действие произошло и со вторым княжеством.
Теперь стало \(3-1+3-1+3=3+3-1+3-1\) княжеств.
Аналогично, если было \(n\) княжеств и они начали делиться, то каждое действие добавляет \(n-1\) княжество.
Послеkдействий получим \(n+k(n-1)\) княжеств.
а) Предположим, что общее число княжеств стало равным 102
\(n+k(n-1)=102\)
Это уравнение с двумя переменными.
Мы умеем решать уравнения в целых числах, если в левой части стоит произведение множителей, а в правой – число. Тогда мы представляем это число в виде произведения простых множителей, взятых в натуральных степенях (по основной теорема арифметики).
Попробуем сделать в левой части произведение множителей.
Для этого перенесём 1 в левую часть.
Получим: \(n-1+k(n-1)=101\)
\((n-1)\cdot (k+1)=101\)
101 - простое число, делится только на себя и на 1;
\(101=101\cdot 1\)
Возможны случаи:
1) \(k+1=101\); \(n-1=1\), тогда \(n=2\), но \(n\geqslant3\) поусловию.
Пришли к противоречию, значит, такой случай невозможен.
2) \(k+1=1\), тогда \(k=0\)
Это означает, что княжества из царства не выходили и не делились, но это противоречит условию. Значит, и этот случай невозможен.
Ответ: нет, не может.
б) Известно, что сразу после одного из делений общее число княжеств было равно 162. Предположим, что в какой‐то момент времени общее число княжеств стало равным 320. Получим систему уравнений:
\(\left\{\begin{matrix}
n+k(n-1)=162 \\
n+m(n-1)=320\end{matrix}\right.\)
Так же, как и в пункте (а), сделаем в левой части каждого уравнения произведение множителей.
\(\left\{\begin{matrix}
n-1+k(n-1)=161 \\
n-1+m(n-1)=319\end{matrix}\right.\)
\(\left\{\begin{matrix}
(n-1)\cdot (k+1)=161 \\
(n-1)\cdot (m+1)=319\end{matrix}\right.\)
Получается, что 161 делится на \( n-1 \) и 319 делится на \( n-1 \).
\( 161=7\cdot 23 \)
\( 319=11\cdot 29 \)
Числа 161 и 319 не имеют общих множителей.
Пришли к противоречию, значит, предположение было неверно.
в) Найдем, сколько княжеств было в самом начале, если сразу после какого‐то из делений общее число княжеств стало ровно в 38 раз больше первоначального.
\(n+k(n-1)=38n\). Приведем подобные:
\(k(n-1)=37n\). Сделаем в левой части произведение множителей.
\(k(n-1)=37n-37+37\)
\(k(n-1)-37(n-1)=37\)
\((k-37)\cdot (n-1)=37\)
37 - простое число, делится только на себя и на 1.
\(n-1=1\), такого не может быть, т.к. \(n\geqslant 3\)
\(k-37=1\), тогда \(n-1=37\),
Значит, \(k=38\); \(n=38\). Было в царстве 38 княжеств, и деление на новые княжества происходило 38 раз.
Ответ:
а) Нет
б) Нет
в) 38