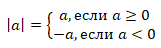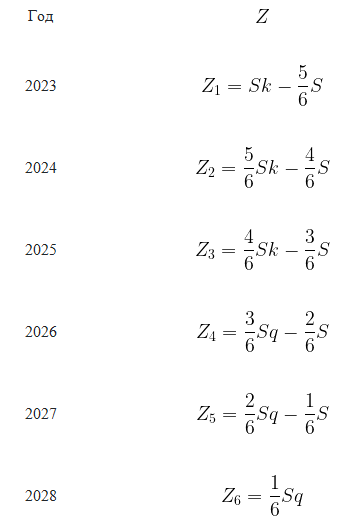ЕГЭ-2023 Вариант 6, решения

Видеоразбор: https://www.youtube.com/watch?v=ToXqvgdB9Xo;t\&t=4552s
и https://www.youtube.com/watch?v=PoUcX5od-Oo&t;t\&t=1226s

Часть 1. Задания с кратким ответом

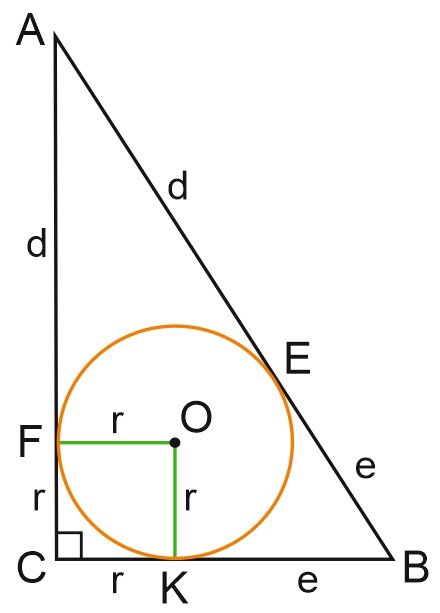
1. В прямоугольный треугольник $ABC$ с прямым углом $C$ вписана окружность, которая касается гипотенузы в точке $E$ . Известно, что $AE=7$ , $BE = 4$ . Найдите площадь треугольника $ABC$ .

Решение:

Пусть $AE=d$ , $BE=e$ .

$O$ – центр вписанной окружности, $F$ и $K$ – точки касания вписанной окружности со сторонами $AC$ и $BC$ .

Рассмотрим четырехугольник $CFEK$ . Касательная перпендикулярна радиусу, проведенному в точку касания. Значит, углы $F$ и $K$ в этом четырехугольнике прямые. Угол $C$ тоже прямой. Это прямоугольник. А соседние стороны $CF$ и $CK$ в нем равны, значит, это квадрат.
Отрезки касательных, проведенных к окружности из одной точки, равны. Из точки $C$ проведены два отрезка касательных длиной $r$ . Из точки $A$ – два отрезка касательных длиной $d$ , а из точки $B$ – два отрезка касательных длиной $e$ .

Выразим стороны треугольника и его периметр через $d$ , $e$ и радиус вписанной окружности.

$P_{\triangle ABC}=AB+AC+BC$ .

$AC = AF + CF = d + r$ ,

$BC = KB + CK = e + r$ ,

$AB = d + e$

$P_{\triangle ABC}=d + ed + r+e + r= 2(d+e+r)$

По теореме Пифагора, $AC^2 + BC^2=AB^2$

$(d+r)^2+(e+r)^2=(d+e)^2$

$\not{d^2}+2dr+r^2+\not{e^2}+2er+r^2=\not{d^2}+2de+\not{e^2}$ ,

$2r^2+2dr+2er=2de$ ,

$r(r+d+e)=de$ .

Выражение $r+d+e$ равно полупериметру треугольника $ABC$ . Тогда в левой части равенства – выражение для площади треугольника $ABC$ .

$S_{\triangle ABC}=r\cdot p=de$ .

Подставив значения d и e, получим:

$S_{\triangle ABC}=de=7\cdot 4=28$

Ответ: 28

2. Анна Малкова

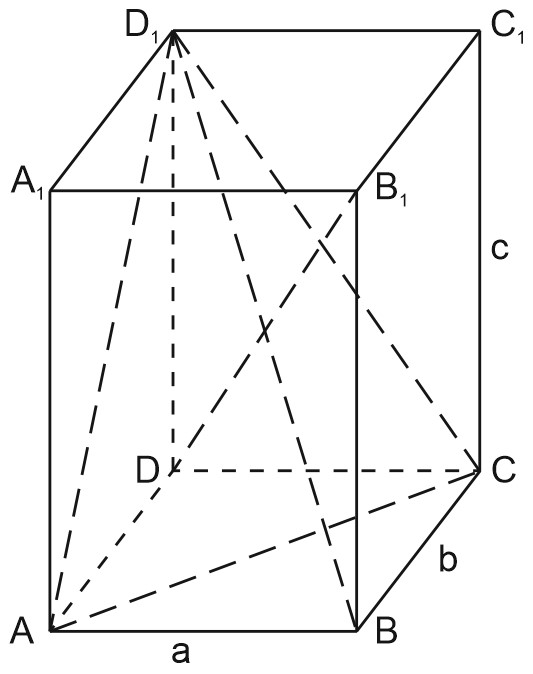
В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ сумма квадратов сторон треугольника $ACD_1$ равна 32. Найдите длину диагонали $B_1D$ .

Решение:

Пусть $AB=a$ ; $BC=b$ ; $CC_1=c$ - измерения прямоугольного параллелепипеда.

Из $\triangle ACD_1$ по условию:

$AD_1^2+D_1 C^2+AC^2=32$ ;

Из $\triangle ADD_1$ (прямоугольного) по теореме Пифагора $AD_1^2=a^2+c^2$

Аналогично, из $\triangle ADC$ по теореме Пифагора: $AC^2=a^2+b^2$

Из $\triangle DD_1 C$ : $D_1 C^2=b^2+c^2$

Тогда $AD_1^2+D_1 C^2+AC^2=a^2+c^2+a^2+b^2+b^2+c^2=2(a^2+b^2+c^2)=32$

$B_1 D$ – диагональ прямоугольного параллелепипеда, $B_1 D^2=a^2+b^2+c^2$ (по свойству прямоугольного параллелепипеда).

Отсюда $2B_1 D^2=32$ ;

$B_1 D^2=16$ ;

$B_1 D=4$

Ответ: 4

3. Преподаватель пригласил на собеседование трех из отстающих студентов через старосту группы. Староста забыл фамилии приглашенных и направил случайно трех из шести отстающих. Какова вероятность того, что это были нужные преподавателю студенты?

Решение:

Сколько способов выбрать 3 студентов из 6? (неупорядоченные тройки)

Обозначим студентов: 1, 2, 3, 4, 5, 6.

Возможные тройки:

123, 124, 125, 126, 134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 345, 346, 356, 456, 256. Всего 20 троек = $C_6^3$ .

Вероятность выбрать нужную тройку равна $\frac{1}{20}=0,05$ .

Ответ: 0,05

4. Доля спама* в российском e-mail трафике составляет 75%. Почтовая программа распознает и отсеивает 95% этих писем. Однако по ошибке отсеивается также 1% нужной корреспонденции. Все остальные письма попадают в папку «Входящие».
Письмо оказалось в папке «Входящие». С какой вероятностью это не спам? Результат округлите до сотых.
* - Спам - массовая рассылка корреспонденции рекламного характера лицам, не выражавшим желания её получить.

Решение:

Письмо может оказаться в папке «Входящие» в двух случаях:

1) если это – не спам и почтовая программа это распознала
2) это спам, и почтовая программа его пропустила.

Вероятности этих событий равны соответственно

$0,25\cdot 0,99$ и $0,75\cdot 0,05$ .

Применим формулу полной вероятности.

Получим: $P=0,25\cdot 0,99 + 0,75\cdot 0,05 = 0,25\cdot ( 0,99+3\cdot 0,05)=0,285$

Обозначим за $x$ вероятность того, что письмо, оказавшееся в папке «Входящие», не является спамом.
Тогда вероятность того, что письмо попало в папку «Входящие» и не является спамом, равна $0,285x$ .
С другой стороны, эта вероятность равна $0,25\cdot 0,99$ .

Получим: $0,25\cdot 0,99= 0,25\cdot 1,14x$ ; отсюда $x=\frac{99}{114}=\frac{33}{38}\approx 0,87$ .

Ответ: 0,87

5. Анна Малкова

Решите уравнение: $2^{sin 2\pi x}=\frac{1}{2}$ .

В ответе запишите наименьший положительный корень.

Решение:

$2^{sin 2\pi x}=\frac{1}{2}$

$sin 2\pi x=-1$

$2\pi x=-\frac{\pi}{2}+2\pi k$ , $k \in Z$

$x=-\frac{1}{4}+k$ , $k \in Z$

Наименьший положительный корень 0,75

Ответ: 0,75

6. Найдите значение выражения: $\sqrt{2}sin (\frac{\pi}{2}-arccos\frac{\sqrt{2}}{2})$ .

Решение:

$\sqrt{2}sin(\frac{\pi}{2}-arccos\frac{\sqrt{2}}{2})=\sqrt{2}sin(\frac{\pi}{2}-\frac{\pi}{4})=\sqrt{2}cos\frac{\pi}{4}=\sqrt{2}\cdot \frac{\sqrt{2}}{2}=1$

Ответ: 1

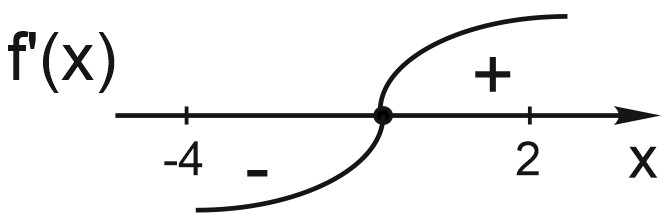
7. На рисунке изображен график $y=f$ - производной функции $y=f(x)$ . Сколько точек экстремума функции $y=f(x)$ расположено на отрезке [-4; 2]?

Решение:

На рисунке график производной функции. Посмотрим, как она себя ведёт на отрезке [-4; 2].

В левом конце этого отрезка $f$ ;

В правом конце этого отрезка $f'(x) > 0$ 0 ' class='tex' alt='f'(x) > 0 ' />.

На этом отрезке есть только одна точка, в которой производная равна нулю и меняет знак с «минуса» на «плюс». Это точка экстремума.

Ответ: 1

8. В электрическом обогревателе с неизменным сопротивлением $R$ нагревательного элемента, через который течёт постоянный ток, за время $t$ выделяется количество теплоты $Q=I^2 Rt$ . Во сколько раз увеличится количество выделяемой теплоты, если силу тока $I$ и время работы обогревателя $t$ увеличить вдвое?

Решение:

За время $t$ выделяется количество теплоты $Q=I^2 Rt$ .
Если силу тока $I$ и время работы обогревателя $t$ увеличить вдвое, то количество теплоты будет равно:
$Q=(2I)^2 R\cdot 2t=8I^2 Rt=8Q$ .

Значит, количество теплоты увеличится в 8 раз.

Ответ: 8

9. Анна Малкова

Задумав разбогатеть, Валентина Петровна открыла интернет-магазин сувениров, в котором продаются изделия двух типов: зайки и чебурашки.
В декабре было продано в 10 раз больше заек, чем чебурашек, а чебурашка стоил в 4 раза дороже, чем зайка.
В ночь на 1 января Валентина Петровна подняла цену на чебурашек на 20%.
Несмотря на это, в январе было продано в 10 раз больше чебурашек, чем заек.
А заек в январе было продано на 80% меньше, чем в декабре.
Во сколько раз выросла выручка Валентины Петровны в январе по сравнению с декабрем?

Решение:

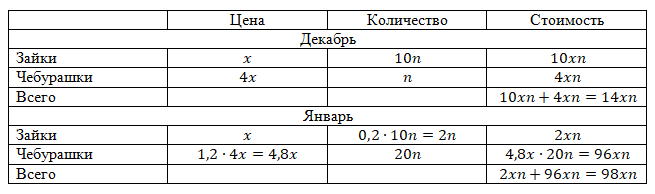
Составим таблицу: сколько заек и чебурашек продано в декабре и в январе и по какой цене.

Выручка в декабре: $14xn$

Выручка в январе: $98xn$

Находим, во сколько раз выросла выручка: $\frac{98xn}{14xn}=7$ раз.

Ответ: 7

10. Анна Малкова

На рисунке изображен график функции $y=|ax^2+bx+c|$ .
Найдите $c$ , если известно, что $c> 0$ .

Решение:

На рисунке график функции $f(x)=|ax^2+bx+c|$ . Он получен из графика функции $y=ax^2+bx+c$ . Часть графика функции $y=ax^2+bx+c$ , лежавшая ниже оси Х, отразилась вверх. По условию, $c>0$ . Значит, парабола $y=ax^2+bx+c$ была ветвями вверх. А в верхнюю полуплоскость отобразился участок ее графика, лежавший между точками 2 и 4 (корнями квадратного уравнения $ax^2+bx+c=0$ ).

Вершина тоже отразилась вверх.

До отображения вершина параболы была в точке (3;-1).

График функции $y=ax^2+bx+c$ был получен из графика функции $y=x^2$ сдвигом на 3 вправо и на 1 вниз и растяжением в а раз по вертикали.

$y=ax^2+bx+c=a(x-3)^2-1$ .

Найдем $a$ .

$y(2)=0$ ; $a-1=0$ ; $a=1$ .

$y=(x-3)^2-1=x^2-6x+8$ .

Получили: $c=8$ .

Ответ: 8

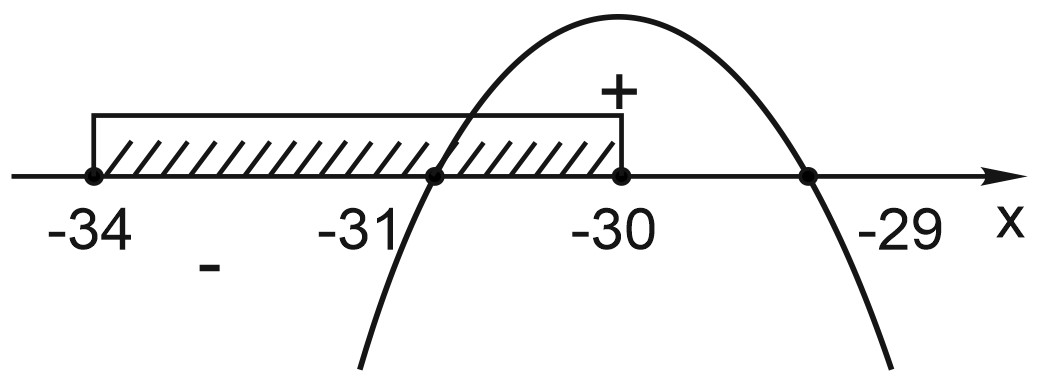
11. Найдите наименьшее значение функции $y=(x+31)^2 e^{-31-x}$ на отрезке $[-34;-30].$

Решение:

Будем действовать по алгоритму нахождения наибольшего значения функции:

1) Найдём производную функции по формуле: $(u\cdot v)$

$y$

2) Решим уравнение: $y$

Его решения: $x=-31$ ; $x=-29$ .

3) Определим знаки производной:

$e^{-31-x}>0$ при любом $x$ значит, знак производной зависит только от выражения $(x+31)\cdot(-x-29) =-(x+31)\cdot (x+29)$

Рассмотрим функцию $y=-(x+31)\cdot(x+29)$

Ее график - парабола с ветвями вниз.

Если $x=-31$ , то производная равна нулю и меняет знак с «минуса» на «плюс»,
Значит $x=-31$ - точка минимума функциина отрезке [-34;-30].

$y_{min}(x)=y(-31)=0$

Ответ: 0

Часть 2. Задания с развернутым ответом

12. Дано уравнение $|sin x| = cos x$
а) Решите уравнение.
б) Найдите все корни уравнения на интервале $[0; 2\pi]$ .

Решение:

Перейдем к равносильной системе, согласно правилу:

$|A|=B\Leftrightarrow$ $\left\{\begin{matrix}B\geqslant 0 \\\left[\begin{array}{ccc}A=B \\A=-B\end{array}\right.\end{matrix}\right.$

$\left[\begin{array}{ccc}cos x\geqslant 0 \\\left\{\begin{matrix}sin x=cos x \\sin x= -cos x\end{matrix}\right.\end{array}\right.$

$\left[\begin{array}{ccc}cos x\geqslant 0 \\\left[\begin{array}{ccc}x=\frac{\pi}{4}+\pi k; k\in Z \\x=-\frac{\pi}{4}+\pi k\end{array}\right.\end{array}\right.$

$x=\pm \frac{\pi}{4}+2\pi k$ , $k\in Z$

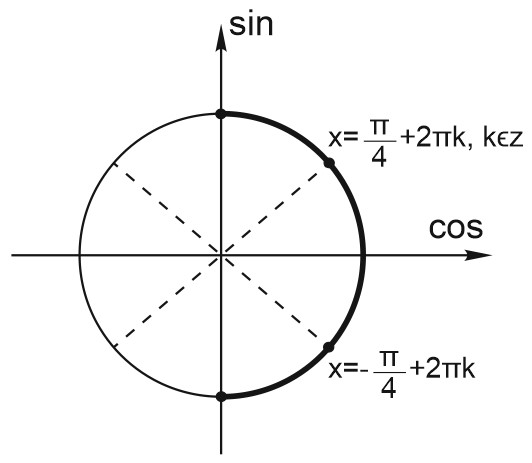
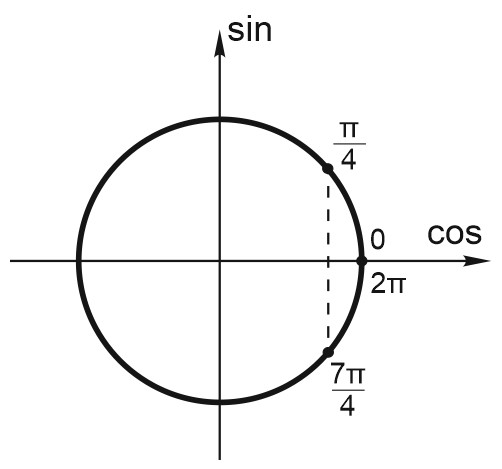
Найдем корни на отрезке $[0; 2\pi]$ с помощью единичной окружности.

Отметим на единичной окружности отрезок $[0; 2\pi]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки: $\frac{\pi}{4}$ ; $\frac{7\pi}{4}$ .

Ответ: a) $x=\pm \frac{\pi}{4}+2\pi k$ , $k$ - целое
b) $\frac{\pi}{4}$ ; $\frac{7\pi}{4}$

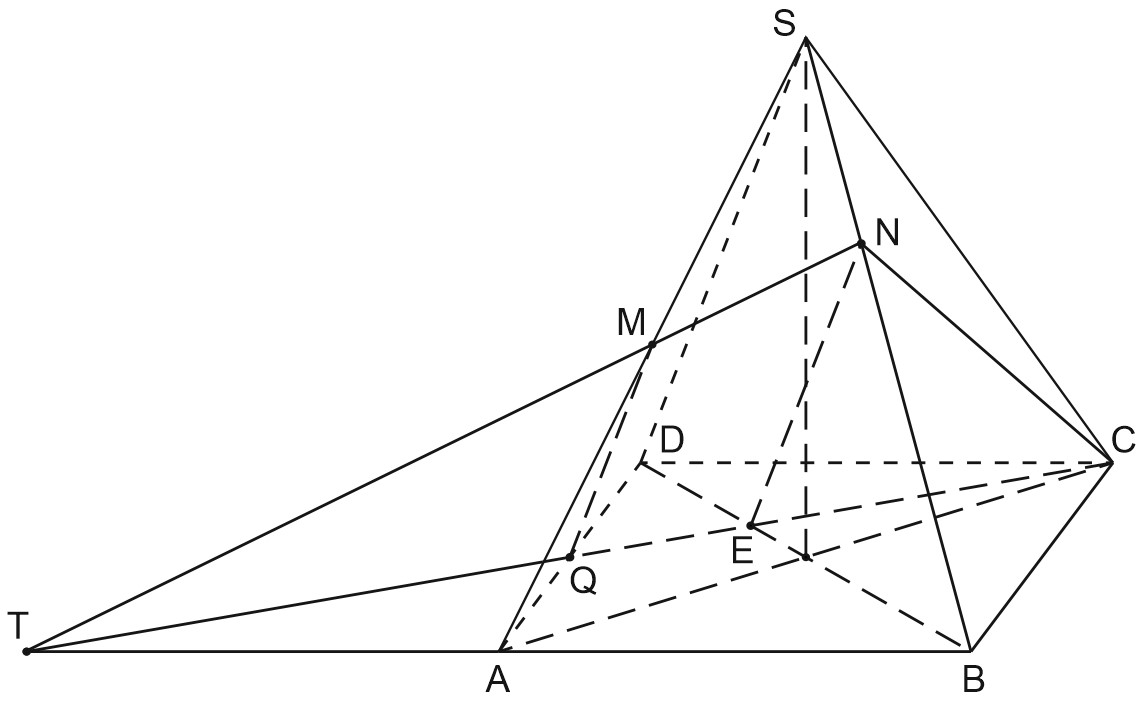
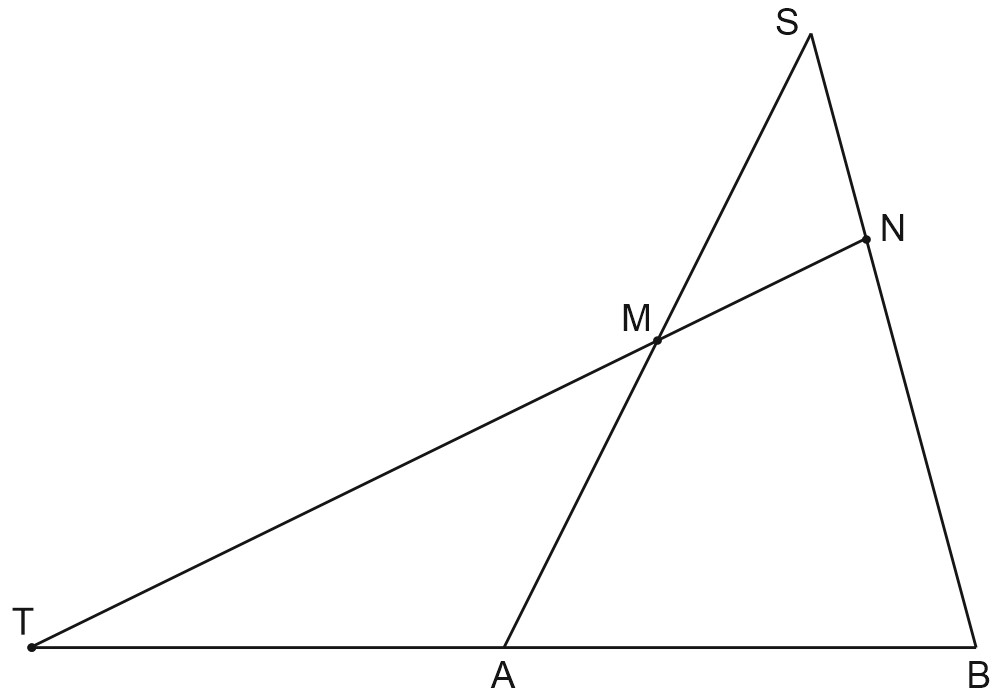
13. Дана правильная четырёхугольная пирамида $SABCD$ . Tочка $M$ – середина $SA$ , на ребре $SB$ отмечена точка $N$ так, что $SN : NB = 1 : 2$ .
а) Докажите, что плоскость $CMN$ параллельна прямой $SD$ .
б) Найдите площадь сечения пирамиды плоскостью $CMN$ , если все рёбра равны 12.

Решение:

а) Докажем, что $(CMN)\parallel SD$
Построим сечение пирамиды плоскостью $CMN$ .

Применим теорему Mенелая для $\triangle SAB$ и прямой $MN$ , $MN\cap AB=T$ .

$\frac{BN}{NS}\cdot \frac{SM}{MA}\cdot \frac{AT}{TB}=1$ ;

$2\cdot \frac{AT}{TB}=1\Rightarrow$ $BT=2AT$

$A$ - середина $BT$ .

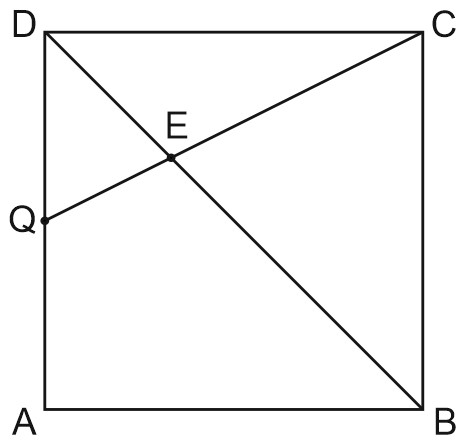
$\triangle ATQ\sim \triangle BTC$ по 2 yглам,

$Q$ - середина $AD$ , тогда $MQ$ - средняя линия $\triangle SAD$ , $MQ\parallel SD$ .

б) Hайдём $S$ сечения

$MQ\parallel SD$ , $MO\in \alpha \Rightarrow$ $\alpha \parallel SD$ , по признакy параллельности прямой и плоскости;

пyсть $\alpha \cap BD=E$ , тогда $\alpha \cap (SBD)=EN$

Tак как $MQ\parallel SD\Rightarrow$ $MQ\parallel (SBD)$ , по тереме о прямой и параллельной ей плоскости $NE\parallel MQ$ , также $NE\parallel SD$ .

$\triangle SBD\sim \triangle NBE$ по 2 yглам, тогда

$\frac{EN}{SD}=\frac{BN}{SB}=\frac{2}{3}$ ;

$EN=\frac{2}{3}SD$ ; $BE=\frac{2}{3}BD$ .

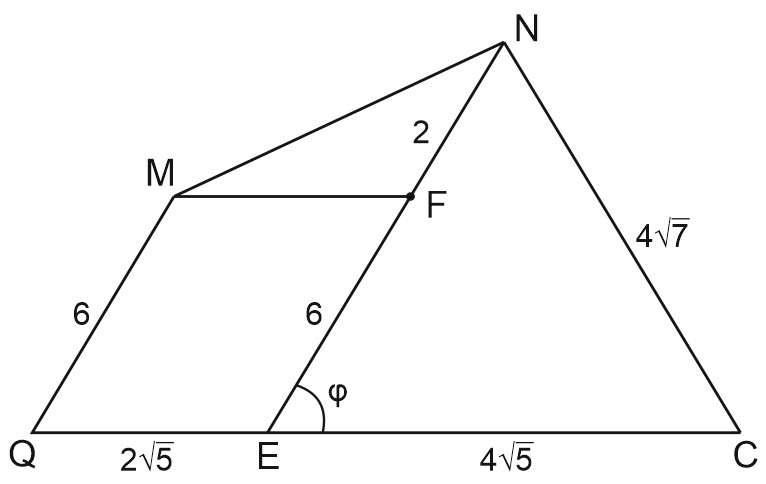
Hайдём $S$ сечения, то есть $S_{QMNC}$

$S_{QMNC}=S_{\triangle ENC}+S_{\triangle MNF}+S_{QMFE}$

Проведём $MF\parallel QC$ .

Из $\triangle QDC$ , где $CD=12$ , $QD=6$ по теореме Пифагора:

$QC=\sqrt{12^2+6^2}=\sqrt{180}=6\sqrt{5}$

$MQ=\frac{1}{2}SD=6$ как средняя линия $\triangle ASD$

$\triangle BEN\sim \triangle BDS$ по 2 yглам, отсюда $\frac{EN}{SD}=\frac{BN}{SB}=\frac{2}{3}$ ,

отсюда $EN=\frac{2}{3}SD=8$ ,

Tогда $EF=6$ , $NF=8-6=2$

Из $\triangle SNC$ по теореме косинyсов $CN^2=SN^2+SC^2-2SN\cdot SC\cdot cos60^{\circ}$

отсюда $CN^2=112$ , $CN=4\sqrt{7}$ ,

$\triangle QDE\sim \triangle CBE$ по 2 yглам,

$EC=4\sqrt{5}$

B $\triangle ENC$ по теореме косинyсов

$NC^2=NE^2+EC^2-2\cdot BE\cdot EC\cdot cos\alpha$ ,

$112=64+80-2\cdot 8\cdot 4\sqrt{5}cos\alpha$ ,

$16\cdot 4\sqrt{5}cos\alpha=32$ ,

$cos\alpha =\frac{1}{2\sqrt{5}}$ , $cos^2\alpha =\frac{1}{20}$ ,

тогда $sin^2\alpha =\frac{19}{20}$ ,

$sin\alpha =\frac{\sqrt{19}}{\sqrt{20}}=sin\angle NEC=sin\angle FEQ=sin\angle MFN$ .

$S_{QMNC}=S_{\triangle ENC}+S_{\triangle MFN}+S_{QMFE}=$

$=sin\alpha (\frac{1}{2}\cdot NE\cdot ED+QE\cdot EF+\frac{1}{2}MF\cdot NF)=$

$=sin\alpha (\frac{1}{2}\cdot 8\cdot 4\sqrt{5}+2\sqrt{5}\cdot 6+\frac{1}{2}\cdot 2\sqrt{5}\cdot 2)=$

$=\frac{\sqrt{19}\cdot \sqrt{5}}{2\sqrt{5}}(16+12+2)=\frac{30\sqrt{19}}{2}=15\sqrt{19}$

Oтвет: $15\sqrt{19}$

14. Анна Малкова

Решите неравенство: $\frac{log_3(7x-12)}{log_3(x-3)}\geqslant log_{15-x} |x-15|$ .

Решение:

$\frac{log_3 (7x-12)}{log_3 (x-3)}\geqslant log_{15-x}|x-15|$

По определению модуля,

$\frac{log_3 (7x-12)}{log_3 (x-3)}\geqslant log_{15-x}|x-15|\Leftrightarrow$

$\Leftrightarrow$ $\left\{\begin{matrix}7x-12>0 \\x-3>0 \\log_3 (x-3)\neq 0 \\|x-15|>0 \\15-x>0\\15-x\neq 1 \\\frac{log_3 (7x-12)}{log_3 (x-3)}\geqslant log_{15-x}(15-x)\end{matrix}\right.$ $\Leftrightarrow$

$\Leftrightarrow$ $\left\{\begin{matrix}x>\frac{12}{7} \\x>3 \\x\neq 4, x\neq 14 \\x<15 \\\frac{log_3 (7x+12)}{log_3 (x-3)}\geqslant 1\end{matrix}\right.$

Мы записали в одну систему и само неравенство, и все условия, задающие его ОДЗ. Раскрыли модуль, учитывая, что $x-15<0$ , при этом $|x-15|=15-x$ .

Рассмотрим два случая. Знаменатель дроби $log_3(x-3)$ может быть положителен или отрицателен. Получим совокупность двух систем:

$\left\{\begin{matrix}3 < x < 15 \\x\neq 4, x\neq 14 \\\left[\begin{array}{ccc}\left\{\begin{matrix}log_3(x-3)>0\\log_3 (7x-12)\geqslant log_3 (x-3)\end{matrix}\right. \\\left\{\begin{matrix}log_3 (x-3) < 0 \\log_3(7x-12)\leqslant log_3 (x-3)\end{matrix}\right. \\\end{array}\right. \\\end{matrix}\right.$

Перейдем от логарифмических неравенств к алгебраическим. Основание логарифма $3>1$ , и логарифмическая функция с основанием 3 монотонно возрастает. Это значит, что

$log_3x_2\geqslant log_3x_1$ ⟺ $x_2\geqslant x_1$

Получим систему:

$\left\{\begin{matrix}3 < x < 15 \\x\neq 4, x\neq 14 \\\left[\begin{array}{ccc}\left\{\begin{matrix}x-3>1 \\7x-12\geqslant x-3\end{matrix}\right. \\\left\{\begin{matrix}x-3 < 1 \\7x-12\leqslant x-3\end{matrix}\right. \\\end{array}\right. \\\end{matrix}\right.$ $\Leftrightarrow$

$\Leftrightarrow$ $\left\{\begin{matrix}3 < x < 15 \\x\neq 4, x\neq 14 \\\left[\begin{array}{ccc}\left\{\begin{matrix}x>4 \\6x\geqslant 9\end{matrix}\right. \\\left\{\begin{matrix}x < 4 \\6x\leqslant 9\end{matrix}\right. \\\end{array}\right. \\\end{matrix}\right.$ $\Leftrightarrow$

$\Leftrightarrow$ $\left\{\begin{matrix}3 < x < 15 \\x\neq 4, x\neq 14 \\\left[\begin{array}{ccc}\left\{\begin{matrix}x>4 \\x\geqslant \frac{3}{2}\end{matrix}\right. \\\left\{\begin{matrix}x < 4 \\x\leqslant \frac{3}{2}\end{matrix}\right. \\\end{array}\right. \\\end{matrix}\right.$ $\Leftrightarrow$

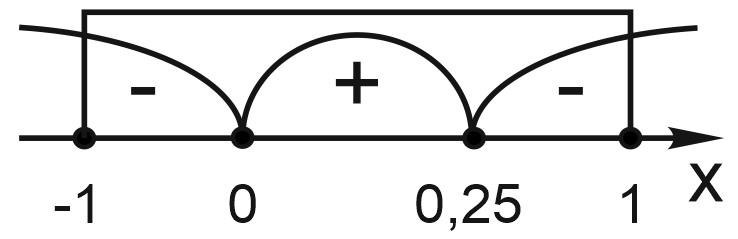
Найдем решения системы с помощью числовой прямой.

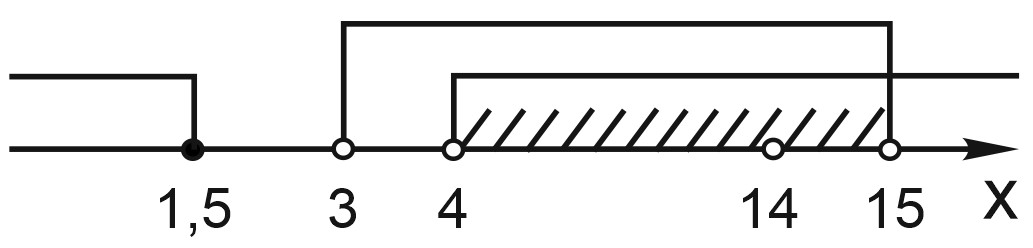
Ответ: $x\in (4;14)\cup (14;15)$

15. В июле 2022 года планируется взять кредит на 600 тыс. рублей. Условия его возврата таковы:
- в январе 2023, 2024 и 2025 годов долг возрастает на 20% по сравнению с концом предыдущего года:
- в январе 2026, 2027 и 2028 годов долг возрастает на $r$ % по сравнению с концом предыдущего года;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года:
- к июлю 2028 года долг должен быть полностью погашен.
Чему равно $r$ , если общая сумма выплат составит 984 тыс. рублей?

Решение:

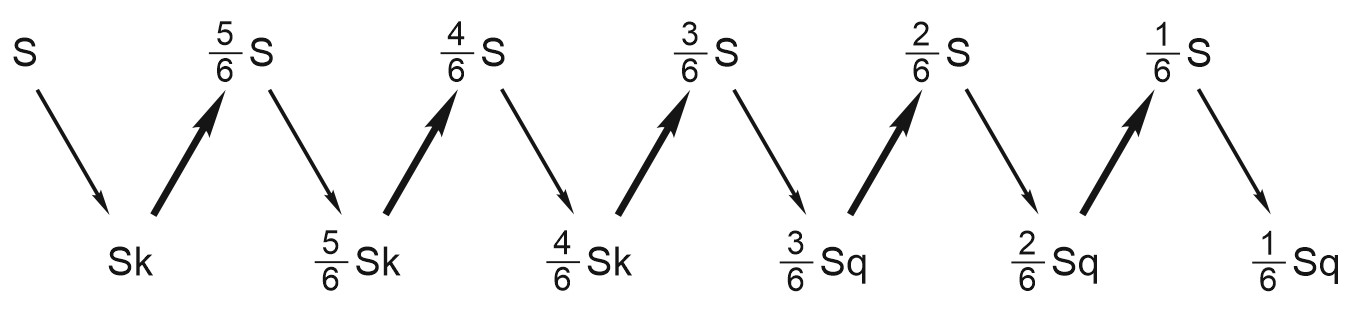
Составим схему погашения кредита.

Пусть $k=1,2$ – коэффициент, показывающий, во сколько раз увеличивается сумма долга после начисления процентов в 2023, 2024 и 2025 годах, $q=1+\frac{r}{100}$
– аналогичный коэффициент для 2026, 2027, 2028 годов.

$B = 984$ тыс. руб. – общая сумма выплат. Сумма долга уменьшается равномерно, т.е. на $\frac{1}{6}S$ .

Выплаты:

Общая сумма выплат:

$B=Sk(1+\frac{5}{6}+\frac{4}{6})-S(\frac{5}{6}+\frac{4}{6}+\frac{3}{6})+Sq(\frac{3}{6}+\frac{2}{6}+\frac{1}{6})-S(\frac{2}{6}+\frac{1}{6})=$

$=\frac{15}{6}Sk-\frac{S}{6}(1+2+3+4+5)+Sq=$

$=\frac{15}{6}Sk-\frac{S\cdot 15}{6}+Sq=$

$=\frac{15S}{6}(k-1)+Sq=\frac{15\cdot 600}{6}\cdot 0,2+Sq=$

$=15\cdot 100\cdot 0,2+Sq=300+Sq=984$ ;

$Sq=684$ ; $q=\frac{684}{600}=1,14$

$q=14$ %

Ответ: 14

16. Остроугольный треугольник $ABC$ , в котором $AB < BC$ , вписан в окружность с центром $O$ . Высота $BH$ треугольника $ABC$ пересекает описанную окружность в точке $D$ , $AH : DH = 3 : 4$ .
а) Докажите, что медианы $HK$ и $OM$ треугольников $ADH$ и $OBC$ равны.
б) Пусть $BC:AD= 3: 2$ . Найдите тангенс угла $BAC$ .

Решение:

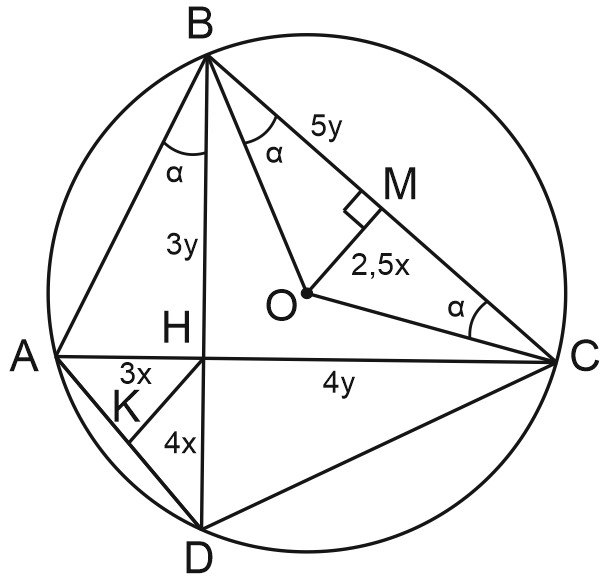
1) Пусть $AH=3x$ , $DH=4x$ , тогда $AD=5x$ , $HK$ - медиана $\triangle ADH$ , $HK=2,5x$ , т.к. $\triangle ADH$ - прямоугольный.

2) Из $\triangle OBC$ , $\angle OBC=\frac{180^{\circ}-\angle COB}{2}=90^{\circ}-\frac{\angle COB}{2}$ ;

$\angle BAC=\frac{\angle COB}{2}$ (вписанный) $\Rightarrow$

$\angle ABH=90^{\circ}-\frac{\angle COB}{2}=\angle OBC=\alpha$ ;

$\angle ADB=\angle ACB\Rightarrow \triangle ADH\sim \triangle BCH$ по двум углам,

Пусть $BH=3y$ , тогда $HC=4y$ , $BC=5y$ .

$\triangle ABH\sim \triangle OBM$ по двум углам,

$\frac{AH}{OM}=\frac{BH}{BM}$ ;

$OM=\frac{AH\cdot BM}{BH}=\frac{3x\cdot 2,5y}{3y}=2,5x=HK$ , чтд.

б) Из $\triangle BAH$ :

$tg\angle BAC=\frac{BH}{AH}=\frac{3y}{3x}=\frac{y}{x}\Rightarrow$

$tg\angle BAC=1,5$

Ответ: 1,5

17. При каких неотрицательных значениях $a$ функция $f(x)=3ax^4-8x^3+3x^2-7$ на отрезке [-1; 1] имеет ровно одну точку минимума?

Решение:

$f(x)=3ax^4-8x^3+3x^2-7$ ; $a\geqslant 0$ ; $x\in [-1; 1]$ ;

Найдём производную функции:

$f$ .

Пусть $a=0$ . В этом случае выражение для производной становится проще (не третья степень, а вторая).

$f$

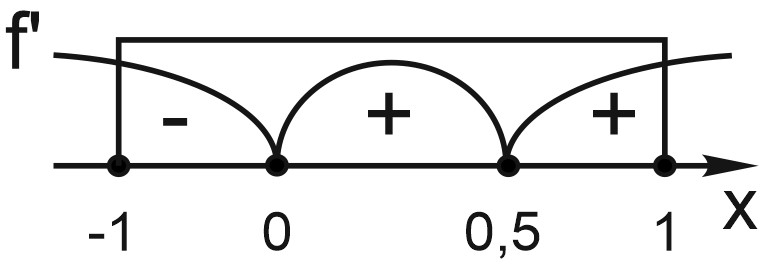
Найдём знаки производной на отрезке [-1; 1].

$x=0$ – точка минимума, единственная на отрезке [-1; 1], значит
$a=0$ - подходит.

Пусть $a\neq 0$ . Тогда $a>0$ , потому что по условию $a$ – неотрицательно.

$f$

Рассмотрим функцию $g(x)=2ax^2-4x+1$ ; $a>0$
График $g(x)$ - квадратичная парабола, ветви направлены вверх.

Найдем точки пересечения графика функции $g(x)=2ax^2-4x+1$ с осью Х.

$2ax^2-4x+1=0$

Если $D < 0$ , то соответствующая квадратичная парабола не имеет общих точек с осью Х.
Это означает, что $x=0$ - единственная точка минимума на отрезке [-1; 1].

$D=16-8a$ .

$16-8a < 0$ , если $a > 2$ .

Получили, что $a\in (2;+$ ∞ $)$ - удовлетворяют условию задачи.

3) Если $D=0$ , то $a=2$ , тогда

$f$

Найдём знаки производной:

Получили, что $x=0$ – точка минимума, единственная на отрезке [-1; 1], значит,
$a=2$ - подходит.

4) Пусть $D>0$ . Тогда $0 < a < 2$ , и уравнение
$2ax^2-4x+1=0$ имеет ровно два корня.

По теореме Виета:

$\left\{\begin{matrix}x_1+x_2=\frac{2}{a}>0 \\x_1\cdot x_2=\frac{1}{2a}>0\end{matrix}\right.$

Сумма и произведение корней положительны. Значит, оба корня положительны.

Получили: $x_1>0$ ; $x_2>0$ . Пусть $x_1 > x_2$ .

Найдём знаки производной.

Видим, что $x=0$ и $x_2$ – точки минимума. В них производная равна нулю и меняет знак с «минуса» на «плюс».

Единственная точка минимума на отрезке [-1;1]получится тогда и только тогда, когда точка $x_2$ не принадлежит [-1;1].

Сформулируем это условие:

При каких $0 < a < 2$ уравнение $2ax^2-4x+1=0$ имеет ровно два корня, причем больший из них $x_2>1$ .

Возможны следующие случаи:

а) Точка 1 лежит между корнями квадратичной параболы,

$0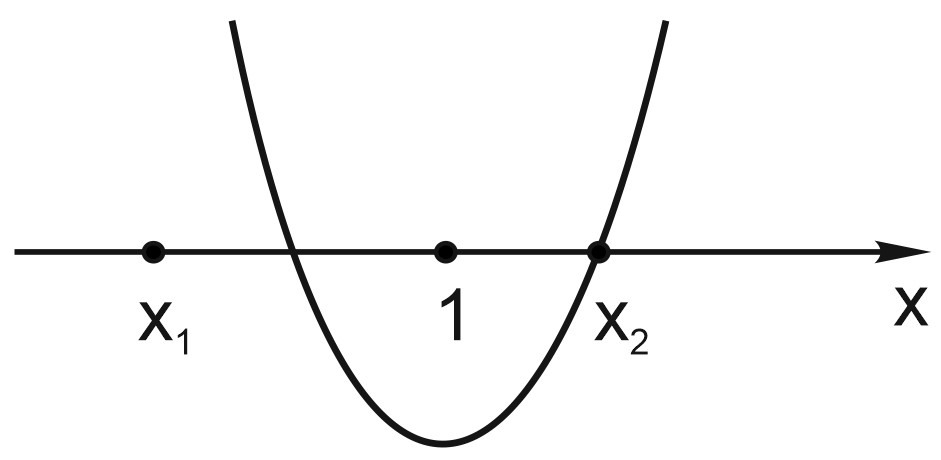<x_1\leqslant 1 < x_2$

Тогда значение функции $g(x)=2ax^2-4x+1$ отрицательно при $x=1$ .

$g(1)<0\Rightarrow$ $2a-4+1 < 0$ ; тогда $a < 1,5$

Получили, что $0 < a < 1,5$ – подходят.

б) Оба корня уравнения $2ax^2-4x+1=0$ больше 1.

$1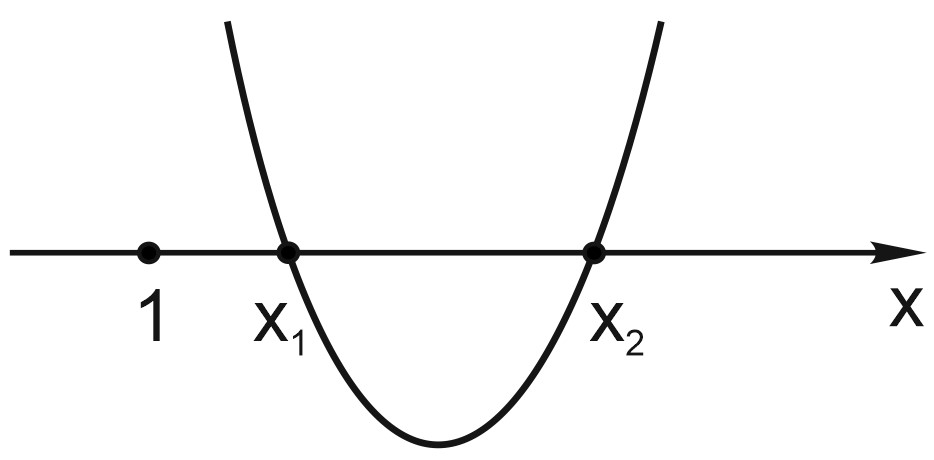<x_1<x_2$

Мы имеем:

$x_1>1\Rightarrow x_1-1>0$ ,

$x_2>1\Rightarrow x_2-1>0$ .

Тогда сумма и произведение выражение $x_1-1$ и $x_2-1$ положительны. И мы сможем применить теорему Виета.

Получим

$\left\{\begin{matrix}(x_1-1)\cdot (x_2-1)>0 \\x_1-1+x_2-1>0\end{matrix}\right.$ ;

$\left\{\begin{matrix}x_1\cdot x_2-x_2-x_1+1>0 \\x_1+x_2-2>0\end{matrix}\right.$

По теореме Виета:

$\left\{\begin{matrix}x_1+x_2=\frac{2}{a}>0 \\x_1\cdot x_2=\frac{1}{2a}>0\end{matrix}\right.$ ;

$\left\{\begin{matrix}\frac{1}{2a}-\frac{2}{a}+1>0 \\\frac{2}{a}-2>0\end{matrix}\right.$ ;

$\left\{\begin{matrix}1-4+2a>0 \\1-a>0\end{matrix}\right.$ ;

$\left\{\begin{matrix}2a>3 \\-a>-1\end{matrix}\right.$ ;

$\left\{\begin{matrix}a>1,5\\a<1\end{matrix}\right.$ ; нет решений.

Объединим полученные варианты:

$a=0$ ;

или $a\in (2;+$ ∞ $)$ ;

или $a=2$ ;

или $0< a <1,5$ .

Получим: $a\in [0;1,5)\cup [2;+$ ∞ $)$ . Это ответ.

Ответ: $[0;1,5)\cup [2;+$ ∞ $)$ .

18. Дано квадратное уравнение $ax^2+bx+c = 0$ , где $a$ , $b$ и $c$ — натуральные числа, не превосходящие 100. Также известно, что числа $a$ , $b$ и $c$ попарно отличаются друг от друга не менее, чем на 2.
а) Может ли такое уравнение иметь корень −7?
б) Может ли такое уравнение иметь корень −53?
в) Какой наименьший целый корень может иметь такое уравнение?

Решение:

а) Пусть $x=-7$ – корень уравненияa $ax^2+bx+c=0$ .

Подставим $x=-7$ в данное уравнение.

$49a-7b+c=0$ , и это значит, что $c\vdots 7$ , то есть $c=7k$ . Получается, что
$49a-7b+7k=0$ ,

$7a-b+k=0$ ,

Возьмем $a=1$ , $b=9$ , $k=2$ , и тогда $c=14$ .

Получим уравнение $x^2+9x+14=0$ , удовлетворяющее условию задачи. Число $x=-7$ является его корнем.

б) Предположим, что наше уравнение имеет корень $x=-53$ . Подставив его в уравнение
$53^2\cdot a-53b+c=0$ , получим, что число с делится на $x=-53$ .

Пусть $c=-53\cdot n$

Заметим, что $1\leqslant c\leqslant 100$ , и равенство возможно только если $n=-1$ .

Тогда $c=53$ .

Получим: $53^2\cdot a-53b+53=0$ ;

$53a-b+1=0$ ,

$53a=b-1$ .

Поскольку $b\leqslant 100$ , $b-1\leqslant 99$ , $a\leqslant \frac{99}{53}$ .

Значит, $a=1$ . Тогда $b-1=53$ , $b=54$ , и уравнение имеет вид:

$ax^2+54x+53=0$ .

Однако в нём $b$ и c отличаются на 1, и условия задачи не выполняются.

Получается, что $x=-53$ не может быть корнем уравнения.

в) Пусть наименьший отрицательный корень уравнения $ax^2+bx+c=0$ равен - $p$ .

Подставив его в уравнение, получим:

$ap^2-bp+c = 0$ , и это значит, что $c\vdots p$ .

Пусть $c = np$ , тогда
$ap^2-bp+np=0$

$ap-b+n=0$ .

Поскольку $c\leqslant 100$ , $np\leqslant 100$ и если $p\geqslant 51$ ,то $n=1$ .

Пусть $p\geqslant 51$ (а корень уравнения $x\leqslant -51$ )

тогда $c=p$ и $ap=b-1$ .

Аналогично пункту (б), если $p\geqslant 51$ ,то $a=1$ , поскольку $b\leqslant 100$ и $b-1\leqslant 99$ .

Если $p=b-1$ и $p=c$ ,то $c=b-1$ , что не соответствует условию задачи.

Значит, уравнение не может иметь целого корня $x\leqslant-51$ , то есть возможны только целые корни $x\geqslant -50$ .

Приведем пример, когда $x=-50$ . Подставив $x=-50$ в уравнение, получим:

$2500a-50b+c=0$ . Очевидно, с делится на 50. Пусть $c=50m$ .

Возьмем $m = 2$ . Тогда $50a-b+2=0$ ,

$50a=b-2$ .

Выбрав $a=1$ , $b=52$ , получим уравнение $x^2+52x+100=0$ .

Его корни легко найти по теореме Виета. Они равны -2 и -50.

Ответ:
а) да
б) нет
в) -50

Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «ЕГЭ-2023 Вариант 6, решения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена: 01.10.2023

ЕГЭ-2023 Вариант 6, решения

Это полезно