Условие задачи
а) Решите уравнение \(\left(1-3tg^2x\right)\sqrt{7{\sin x}}=0.\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\displaystyle \left[-2\pi ; -\frac{\pi }{2}\right].\)
Решение
а) \(\left(1-3tg^2x\right)\sqrt{7{\sin x}}=0.\) Так как \({\sin x}\) стоит под корнем, то он неотрицателен, а наличие тангенса добавляет ограничение \({\cos x}\ne 0,\) поэтому уравнение равносильно системе \(\displaystyle \left\{ \begin{array}{c}
{\cos x}\neq 0, \\
{\sin x}\geq 0, \\
\left[ \begin{array}{c}
{\sin x}=0, \\
1-3tg^2x=0; \end{array}
\right. \end{array}
\right.\Leftrightarrow \left\{ \begin{array}{c}
{\sin x}\geq 0, \\
\left[ \begin{array}{c}
{\sin x}=0, \\
tg^2x=\displaystyle \frac{1}{3}; \end{array}
\right. \end{array}
\right.\Leftrightarrow \left\{ \begin{array}{c}
{\sin x}\geq 0, \\
\left[ \begin{array}{c}
{\sin x}=0, \\
tgx=\displaystyle \frac{\sqrt{3}}{3}, \\
tgx=-\displaystyle \frac{\sqrt{3}}{3}. \end{array}
\right. \end{array}
\right.\)
Ограничение \({\cos x}\neq 0\) уже можно убрать, так как синус и косинус не могут равняться нулю одновременно.
Изобразим тригонометрический круг и на нём отметим точки, соответствующие значениям \(\displaystyle tgx=\pm \frac{\sqrt{3}}{3}, \; {\sin x}=0.\)
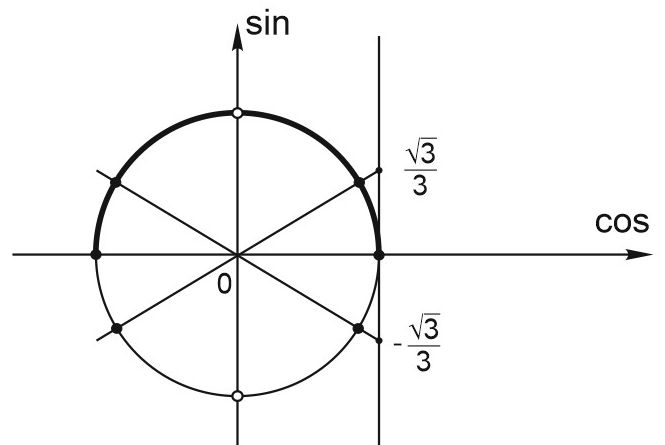
С учётом неотрицательности \({\sin x}\) получаем следующие серии решений
\(\displaystyle x=\pi n, \; n\in Z; \; x=\frac{\pi }{6}+2\pi k, \; k\in Z; \; x=\frac{5\pi }{6}+2\pi m, \; m\in Z.\)
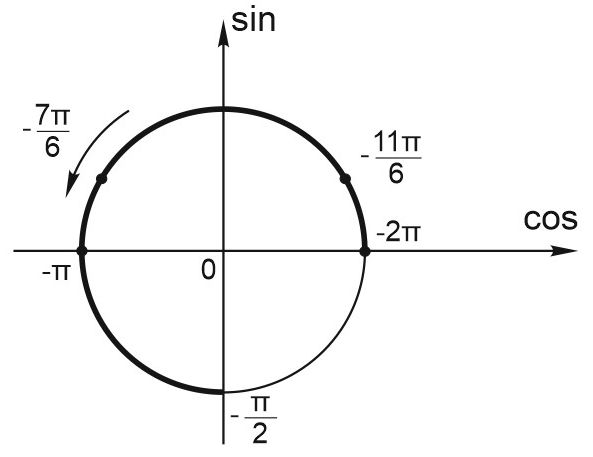
б) С помощью тригонометрического круга отберём корни, принадлежащие отрезку \(\left[-2\pi ; \displaystyle -\frac{\pi }{2}\right].\)
Видим, что отрезку принадлежат точки \(-2\pi ; \; -2\pi +\displaystyle \frac{\pi }{6}=-\frac{11\pi }{6}; \; -\pi -\frac{\pi }{6}=-\frac{7\pi }{6}; \; -\pi .\)
Ответ:
а) \(x=\pi n, \; n\in Z;\) \(\displaystyle x=\frac{\pi }{6}+2\pi k, \; k\in Z;\) \(\displaystyle x=\frac{5\pi }{6}+2\pi m, \; m\in Z\).
б) \(-2\pi ;\) \(\displaystyle -\frac{11\pi }{6};\) \(\displaystyle -\frac{7\pi }{6}; -\pi .\)






























