Условие задачи
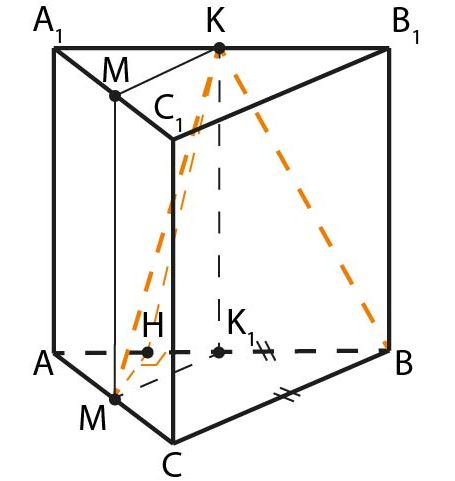
В основании прямой треугольной призмы \(ABCA_1B_1C_1\) лежит равнобедренный треугольник \(ABC\) с равными сторонами \(AB\) и \(BC.\) Точки \(K\) и \(M\) — середины рёбер \(A_1B_1\) и \(AC\) соответственно.
а) Докажите, что \(KM=KB.\)
б) Найдите угол между прямой \(KM\) и плоскостью \(ABB_1,\) если \(AB = 8,\) \(AC = 6\) и \(1\) \(AA_1=3.\)
Решение
а) Пусть \(M_1\) — проекция точки \(M\) на верхнее основание, а \(K_1\) — проекция точки \(K\) на нижнее основание призмы, тогда \(MM_1\parallel AA_1\) и \(K_1K\parallel AA_1.\)
Соединяя точки \(K, \; M_1, \; M, \; K_1\) и \(K,\) получаем прямоугольник \(K_1K\parallel M_1M,\) в плоскости которого лежит прямая \(MK.\)
\(KB\) — гипотенуза прямоугольного треугольника \(KK_1B,\) а \(KM\) — гипотенуза прямоугольного треугольника \(KK_1M.\) Докажем, что эти треугольники равны.
\(\displaystyle K_1B=\frac{1}{2}AB\) по построению; \(K_1M\) — средняя линия \(\triangle ABC\): \(K_1M\parallel BC\) и
\(\displaystyle K_1M=\frac{1}{2}BC=\frac{1}{2}AB,\) следовательно, \(K_1B=K_1M, \; K_1K\) — общая, прямоугольные треугольники \(KK_1B\) и \(KK_1M\) равны, а значит, \(KM=KB,\) что и требовалось доказать.
б) Угол \(\varphi \) между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость. Точка \(K\) лежит в плоскости \(\left(ABB_1\right),\) найдём проекцию точки \(M\) на эту плоскость. В плоскости \(\left(ABC\right)\) проведём \(MH\) перпендикулярно \(AB.\)
\(\left. \begin{array}{c}
MH\in \left(ABC\right) \\
AA_1\bot \left(ABC\right) \end{array}
\right\}\Rightarrow AA_1\bot MH,\)
\(\left. \begin{array}{c}
MH\bot AA_1 \\
MH\bot AB \end{array}
\right\}\Rightarrow MH\bot \left(ABB_1\right)\) по признаку перпендикулярности прямой и плоскости.
На плоском чертеже найдём такую точку \(H,\) что \(MH\bot AB.\)
Пусть \(CL\) — высота \(\triangle ABC,\) тогда \(MH\parallel CL\) и проходит через середину \(AC,\) значит, \(MH\) — средняя линия и \(\displaystyle MH=\frac{1}{2}CL.\)
\(CL\) найдём из \(\triangle ABC\) по методу площадей \(\displaystyle S_{\triangle ABC}=\frac{1}{2}AC\cdot BM=\frac{1}{2}AB\cdot CL.\)
Треугольник \(BCM\) прямоугольный, так как в равнобедренном \(\triangle ABC\) медиана \(BM\) является высотой.
По теореме Пифагора:
\(BM=\sqrt{BC^2-MC^2}=\sqrt{64-9}=\sqrt{55}.\)
\(AC\cdot BM=AB\cdot CL,\) \(\displaystyle CL=\frac{6\cdot \sqrt{55}}{8}=\frac{3\sqrt{55}}{4}.\)
\(\displaystyle HM=\frac{1}{2}CL=\frac{3\sqrt{55}}{8}. \; HM\) — перпендикуляр, \(KH\) — проекция, \(\varphi =\angle MKH.\)
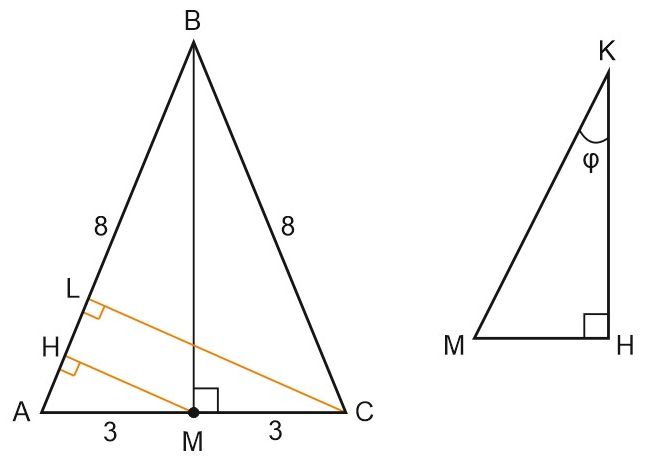
Угол \(\varphi \) найдём из прямоугольного \(\triangle MKH\) \(\displaystyle \left(\left. \begin{array}{c}
MH\bot \left(ABB_1\right) \\
KH\in \left(ABB_1\right) \end{array}
\right\}\Rightarrow MH\bot KH\right).\)
\(\displaystyle HM=\frac{3\sqrt{55}}{8},\)
\(MK=KB=\sqrt{K_1K^2+K_1B^2}=\sqrt{3^2+4^2}=5,\) тогда
\(\displaystyle {\sin \varphi }={\sin \angle }MKH=\frac{3\sqrt{55}}{8\cdot 5}=\frac{3\sqrt{55}}{40}, \; \displaystyle \varphi ={\arcsin \frac{3\sqrt{55}}{40}}.\)
Ответ:
б) \(\displaystyle {\arcsin \frac{3\sqrt{55}}{40}}.\)




























