Условие задачи
В треугольнике \(ABC\) проведены биссектрисы \(BM\) и \(CN.\) Оказалось, что точки \(B, \; C, \; M\) и \(N\) лежат на одной окружности.
а) Докажите, что треугольник \(ABC\) равнобедренный.
б) Пусть \(P\) — точка пересечения биссектрис треугольника \(ABC.\) Найдите площадь четырёхугольника \(AMPN,\) если \(MN:BC = 2:5,\) а \(BN =14.\)
Решение
а) Обозначим половинки углов \(B\) и \(C\) через \(\beta \) и \(\gamma .\)
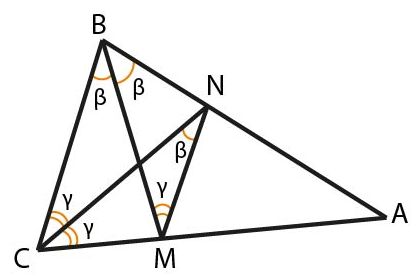
Четырёхугольник \(CBNM\) вписан в окружность, поэтому \(\angle CBM=\angle CNM=\beta , \; \angle BCN=\angle BMN=\gamma ,\) как вписанные в окружность и опирающиеся на равные дуги.
Аналогично \(\angle MCN=\angle MBN,\) т. е. \(\beta =\gamma \) и \(\angle BCA=2\gamma =2\beta =\angle CBA,\) следовательно, \(\vartriangle ABC\) — равнобедренный, что и требовалось доказать.
б) Переделаем чертёж согласно пункту (а).
1) \(\triangle BMC=\triangle CNB\) по стороне и двум углам, значит, \(MC=NB=14,\) а \(AM=AN,\) поэтому \(\triangle ANM\sim \triangle ABC, \; \angle ANM=\angle ABC,\) и \(NM\parallel BC.\)
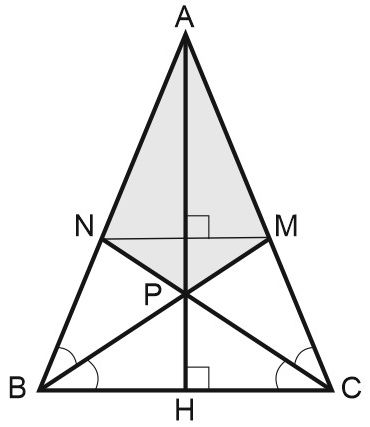
Из подобия треугольников \(\triangle ANM\sim \triangle ABC\) получаем \(\displaystyle \frac{NM}{BC}=\frac{AN}{AB}.\)
Пусть \(AN=x,\) значит, \(AB=14+x\) и из равенства отношений \(\displaystyle \frac{x}{14+x}=\frac{2}{5}\) получаем \(\displaystyle x=\frac{28}{3},\) а \(\displaystyle AB=14+\frac{28}{3}=\frac{70}{3}.\)
2) В \(\vartriangle ABC \; BM\) — биссектриса, и по свойству биссектрисы имеем
\(\displaystyle \frac{AB}{BC}=\frac{AM}{MC}=\frac{28}{3\cdot 14}=\frac{2}{3},\) значит, \(\displaystyle \frac{70}{3\cdot BC}=\frac{2}{3}\) и \(BC=35.\)
\(\displaystyle \frac{MN}{BC}=\frac{2}{5}, \; MN=\frac{2\cdot 35}{5}=14.\)
Пусть прямая \(AP\) пересекает \(BC\) в точке \(H, \; AH\) — биссектриса, медиана и высота, \(\displaystyle BH=\frac{BC}{2}=\frac{35}{2}\) и \(AH=\sqrt{AB^2-BH^2}=\sqrt{{\left(\displaystyle \frac{70}{3}\right)}^2-{\left(\displaystyle \frac{35}{2}\right)}^2}=\displaystyle \frac{35\sqrt{7}}{6}.\)
3) В \(\vartriangle ABH\) \(BP\) — биссектриса, по свойству биссектрисы \(\displaystyle \frac{AP}{PH}=\frac{AB}{BH}, \; \frac{AP}{AH-AP}=\frac{AB}{BH}.\) Пусть \(AP=y,\) получаем уравнение
\(\displaystyle \frac{y}{AH-y}=\frac{70\cdot 2}{3\cdot 35}, \; 7y=4AH, \; y=4\cdot \frac{35\sqrt{7}}{6\cdot 7}=\frac{10\sqrt{7}}{3}, \; \displaystyle AP=\frac{10\sqrt{7}}{3}.\)
Так как \(\left. \begin{array}{c}
AH\bot BC \\
BC\parallel MN \end{array}
\right\}\Rightarrow AH\bot MN,\) то в четырёхугольнике \(AMPN\) диагонали перпендикулярны и известны, поэтому
\(\displaystyle S_{AMPN}=\frac{1}{2}AP\cdot MN=\frac{1}{2}\cdot \frac{10\sqrt{7}}{3}\cdot 14=\frac{70\sqrt{7}}{3}.\)
Ответ:
б) \(\displaystyle \frac{70\sqrt{7}}{3}.\)






























