Условие задачи
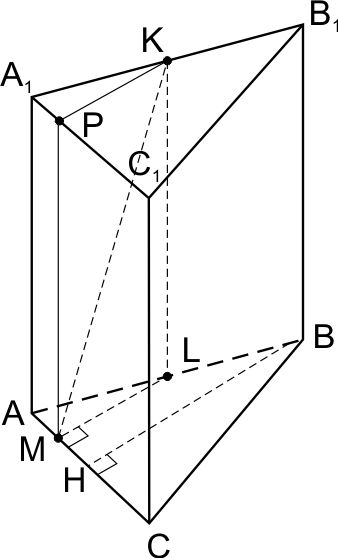
Дана прямая треугольная призма \(ABCA_1B_1C_1 .\) Известно, что \(AB=BC\). Точка \(K\) — середина ребра \(A_1B_1 ,\) а точка \(M\) лежит на ребре \(AC\) и делит его в отношении \(AM:MC = 1:3.\)
а) Докажите, что прямая \(KM\) перпендикулярна прямой \(AC\).
б) Найдите расстояние между прямыми \(KM\) и \(A_1C_1 ,\) если \(AB = 6, \; AC = 8\) и \(AA_1=3 .\)
Решение
а) Укажем какую-нибудь плоскость, содержащую прямую \(KM\). Для этого возьмём точку \(L\) — середину \(AB\) и через точки \(K, \; M\) и \(P\) проведём плоскость. Эта плоскость пересекает грань \(AA_1B_1B\) по прямой \(KL\), параллельной прямой \(AA_1 ,\) и следовательно, как и \(AA_1\), перпендикулярна плоскости \(\left(ABC\right) .\)
Пусть \(H\) — середина \(AC\). В равнобедренном треугольнике \(ABC\) медиана \(BH\) является высотой, поэтому \(BH\bot AC .\) Точка \(M\), делящая \(AC\) в отношении \(1:3\), является серединой \(AH\). Таким образом, \(LM\) — средняя линия \(\vartriangle ABH ,\) поэтому она параллельна \(BH\), а значит, перпендикулярна \(AC\).
По признаку перпендикулярности прямой и плоскости
\(\left. \begin{array}{c}
KL\bot AC \\
LM\bot AC \end{array}
\right\}\Rightarrow AC\bot \left(KLM\right) .\)
\(\left. \begin{array}{c}
KM\in \left(KLM\right) \\
\left(KLM\right)\bot AC \end{array}
\right\}\Rightarrow KM\bot AC .\) Что и требовалось доказать.
б) Достроим сечение призмы плоскостью \(\left(KLM\right) .\) Линия её пересечения с верхней гранью \(A_1B_1C_1\) параллельна \(LM\) (как линии пересечения двух параллельных плоскостей третьей) \(P\in A_1C_1 \cap \left(KLM\right) .\) Соединим точки \(P\) и \(M\).
Найдём расстояние между скрещивающимися прямыми \(KM\) и \(A_1C_1\) как длину их общего перпендикуляра.
\(\left. \begin{array}{c}
A_1C_1\parallel AC \\
AC\bot \left(KLM\right) \end{array}
\right\}\Rightarrow A_1C_1\bot \left(KLM\right) ,\) следовательно, \(A_1C_1\)перпендикулярна любой прямой, лежащей в плоскости \(\left(KLM\right) .\)
Построим такую прямую в плоскости \(\left(KLM\right) ,\) которая будет перпендикулярна и \(KM\).
Из точки \(P\) опустим перпендикуляр \(PT\) на прямую \(KM\).
\(\left. \begin{array}{c}
A_1C_1\bot \left(KLM\right) \\
PT\in \left(KLM\right) \end{array}
\right\}\Rightarrow A_1C_1\bot PT , \; PT\bot KM ,\) значит, \(PT\) — общий перпендикуляр скрещивающихся прямых.
Чтобы найти его длину, рассмотрим четырёхугольник \(PKLM .\)
Это прямоугольник, так как \(KL\bot PK,KL\bot ML\) (см. а).
\(\left. \begin{array}{c}
ML\bot AA_1 \\
ML\bot AC \end{array}
\right\}\Rightarrow ML\bot \left(ACC_1\right)\Rightarrow ML\bot PM\) и \(PK=ML .\)
\(PT\) — высота прямоугольного треугольника \(PKM . \; PM=KL=AA_1=3 , \; ML\) найдём из \(\vartriangle ABH .\)
\(AB=6, \; AC=8, \; AH=4,\) тогда по теореме Пифагора \(BH=\sqrt{6^2-4^2}=\sqrt{20}=2\sqrt{5} , \; ML=\sqrt{5} , \; MK=\sqrt{5+9}=\sqrt{14} .\)
По методу площадей \(\displaystyle PK\cdot MP=KM\cdot PT , \; PT=\frac{PK\cdot MP}{MK}=\frac{\sqrt{5}\cdot 3}{\sqrt{14}}=\frac{3\sqrt{70}}{14} .\)
Ответ:
б) \(\displaystyle \frac{3\sqrt{70}}{14} .\)