13. а) Решите уравнение \(25^{-\sqrt {1-cos^2x }}-25^{sin x}=-\displaystyle \frac{24}{5}.\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left [-3π;-\displaystyle \frac{3π}{2}\right ].\)
Решение:
\( \sqrt{1-cos^{2x} }=|sinx|.\)
\( 25^{-|sinx|}-25^{sinx} =-\displaystyle \frac{24}{5}.\)
1) \( sinx=0\), тогда \( 25 ^{\circ}-25 ^{\circ}=1-1=0≠-\displaystyle \frac{24}{5}.\)
2) \(sinx < 0\), тогда \(25^{sinx} -25^{sinx} =0≠-\displaystyle \frac{24}{5}\) - нет решений.
3) \(sinx > 0\), тогда \(25^{sinx} -25^{-sinx}=\displaystyle \frac{24}{5}.\)
Замена: \(25^{sinx}=t, \ t > 0\),
\(t-\displaystyle \frac{1}{t}=\frac{24}{5}; \ t^{2}-\displaystyle \frac{24}{5}t-1=0\);
\(5t^{2}-24t-5=0\);
\(D=576+100=676\);
\(\sqrt{D}=26\),
\(t=\displaystyle \frac{(24±26)}{10}\);
\(t_1=5; \ t_2 < 0\) – не подходит, т. к. \(t > 0.\)
\(25^{sinx}=5\);
\(25^{sinx} =25^{\frac{1}{2}}; \ sinx=\displaystyle \frac{1}{2}\), при этом \(sinx > 0.\)
\(x=\displaystyle \frac{π}{6}+2πn, \ n∈z\) или \(x=\displaystyle \frac{5π}{6}+2πn.\)
б) С помощью двойного неравенства отберем корни.
\(x=-2π+\displaystyle \frac{π}{6}=-\frac{11π}{6}.\)
14. В правильной четырёхугольной призме \(ABCDA_1 B_1 C_1 D_1\) сторона \(AB\) основания равна 7, а боковое ребро \(AA_1\) равно \(\sqrt7\). На рёбрах \(BC\) и \(C_1 D_1\) отмечены точки \(K\) и\(L\) соответственно, причём \(BK=C_1 L=3\). Плоскость \(γ\) параллельна прямой \(BD\) и содержит точки \(K\) и \(L\).
а) Докажите, что прямая \(A_1 C\) перпендикулярна плоскости \(γ.\)
б) Найдите объём пирамиды, вершина которой – точка \(A\), а основание – сечение данной призмы плоскостью \(γ.\)
Решение:
Проведем \(KN||BD\).
\(∆CKN∼∆CBD\) по двум углам.
\(\displaystyle \frac{CK}{BC}=\frac{CN}{CD}=\frac{4}{7}\);
\(CK=CN=4.\)
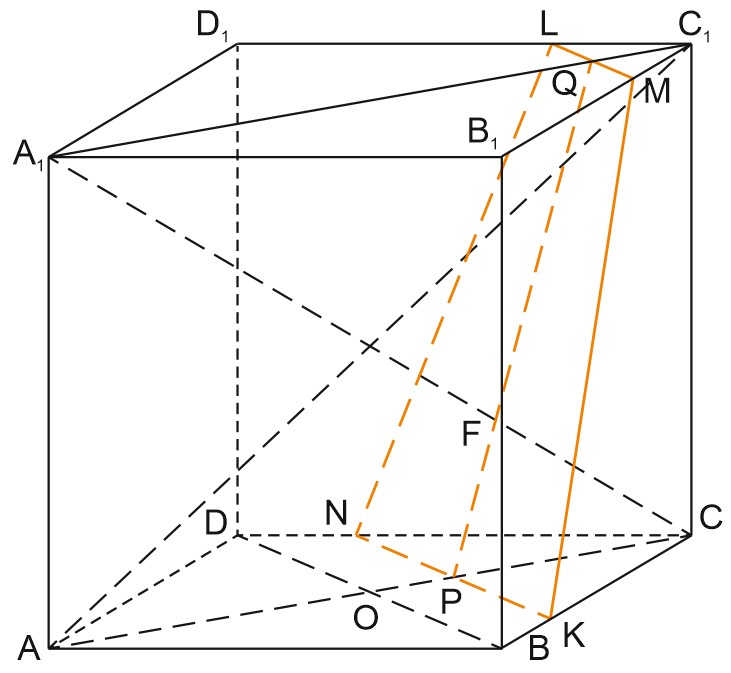
Проведём \(LM||B_1 D_1\).
\(\displaystyle \frac{C_1 M}{C_1 B_1}=\frac{C_1 L}{C_1 D_1}=\frac{3}{7}\);
\(C_1 M=C_1 L=3\);
\(LM||NK\) как линии пересечения параллельных плоскостей третьей плоскостью сечения – трапеция \(KMLN\).
\(AC⊥BD⇒AC⊥NK.\)
Тогда \(A_1 C⊥NK\), по теореме о трех перпендикулярах.
Пусть \(A_1 C∩(KLM)=F\);
\(AC∩KN=P\),
\(A_1 C_1∩LM=Q\),
\(AC∩BD=O\),
\(A_1 C_1∩B_1 D_1=O_1\),
\(∆CPK∼∆COB\) по 2 углам, \(⇒ CP=\displaystyle \frac{4}{7} CO\).
Аналогично, \(C_1 Q=\displaystyle \frac{3}{7} C_1 O_1\).
\(A_1 C_1=AC=7\sqrt2\).
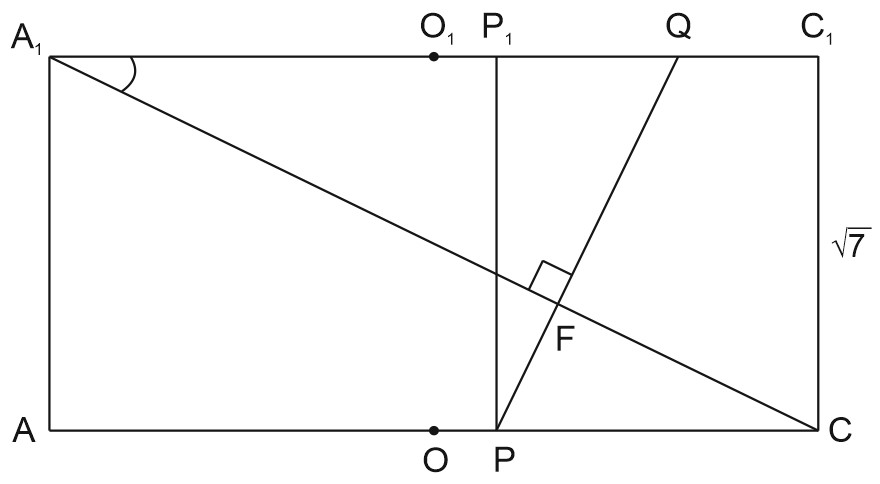
Докажем, что \(QP⊥A_1 C\).
Рассмотрим \(∆A_1 FQ\);
\(tg∠CA_1 C_1=tg∠FA_1 Q=\displaystyle \frac{\sqrt7}{7\sqrt2}=\frac{1}{\sqrt{14}}.\)
Проведем \(PP_1 ||CC_1.\)
Из \(∆PP_1 Q\):
\(P_1 Q=\displaystyle \frac{7\sqrt2}{2}\cdot\frac{1}{7}=\frac{\sqrt2}{2}\);
\(tg∠P_1 QP=tg∠A_1 QF=\displaystyle \frac{\sqrt7\cdot2}{\sqrt2}=\sqrt14\);
\(tg∠A_1 QF=\displaystyle \frac{1}{tg∠QA_1 F}=ctg∠QA_1 F=tg \left (\displaystyle \frac{π}{2}-∠QA_1 F\right ).\)
Так как углы \(A_1 QF\) и \(QA_1 F\) острые,
\(∠A_1 QF=\displaystyle \frac{π}{2}-∠QA_1 F\);
\(∠A_1 QF+∠QA_1 F=\displaystyle \frac{π}{2}⇒A_1 C⊥PQ\).
По признакам перпендикулярности прямой и плоскости \(A_1 C⊥(KML)\).
б) Найдем \(V_{A_1 KMLN}.\)
Так как \(A_1 C⊥(KML)\);
\(V_{A_1 KMLN}=\displaystyle \frac{1}{3} S_∆KMLN\cdot A_1 F\),
\(A_1 F\) – расстояние от \(A_1\) до плоскости \((KML).\)
Из \(∆A A_1 C: \ A_1 C=\sqrt{AA_1^{2}+AC^{2}}=\sqrt{105}\);
\(∆AA_1 C∼ ∆FPC\), отсюда
\(FC=\displaystyle \frac{AC\cdot PC}{A_1 C}=\frac{4\sqrt{105}}{15}\);
\(A_1 F=\displaystyle \frac{11\sqrt{105}}{15}\).
Из \(∆PP_1 Q\):
\(PQ=\displaystyle \frac{\sqrt30}{2}\);
\(NK=4\sqrt2, \ LM=3\sqrt2\),
\(V_{A_1 KMLN}=\displaystyle \frac{77\sqrt7}{6}\).
15. Решите неравенство \(\displaystyle \frac{log_5(x+1)-log_5(5-x)}{log_5^{2}x^{2}+3 log_5x^{4}+9} ≤0.\)
Решение:
Упростим знаменатель:
\(3 log_2x^{4}=6 log_2x^{2}\);
\(log_5^{2}x^{2}+6 log_5x^{2}+9 =(log_5x^{2}+3 )^{2};\)
\(\displaystyle \frac{log_5 (x+1)-log_5 (5-x)}{(log_5x^{2}+3 )^{2} }≤0.\)
ОДЗ: \( \left\{\begin{matrix} x+1 < 0,\\ 5-x < 0,\\x\neq 0,\\ log_5x^{2}≠-3;\end{matrix}\right.\)
\( \left\{\begin{matrix} -1 < x < 5,\\x\neq 0,\\ x^{2}≠\displaystyle \frac{1}{125}.\end{matrix}\right.\)
Неравенство равносильно системе:
\( \left\{\begin{matrix} -1 < x < 5,\\ x^{2}≠\displaystyle \frac{1}{125},\\x\neq 0,\\ log_5 (x+1)-log_5 (5-x)≤0;\end{matrix}\right.\)
\( \left\{\begin{matrix} -1 < x < 5,\\x\neq 0,\\ x≠\pm\displaystyle \frac{1}{5\sqrt{5}},\\ log_5 (x+1)≤ log_5 (5-x).\end{matrix}\right.\)
Функция \(y=log_5 t\) монотонно возрастает, поэтому, если
\(log_5t_1≤log_5t_2\), то \(t_1≤t_2.\)
При \(t_1 > 0, \ t_2 > 0\)
\( \left\{\begin{matrix} -1 < x < 5,\\x\neq 0,\\ x≠\pm\displaystyle \frac{1}{5\sqrt{5}},\\ x+1≤5-x; \end{matrix}\right.\)
\( \left\{\begin{matrix} -1 < x < 5,\\x\neq 0,\\ x≠\pm\displaystyle \frac{1}{5\sqrt{5}},\\ x≤2.\end{matrix}\right.\)
\(-1 < -\displaystyle \frac{1}{5\sqrt{5}} < 0;\)
\(0 < \displaystyle \frac{1}{5\sqrt{5}} < 2.\)
Ответ: \(x∈\left (-1;-\displaystyle \frac{1}{5\sqrt{5}}\right )∪\left (-\displaystyle \frac{1}{5\sqrt{5}};0\right )∪\left (0;\displaystyle \frac{1}{5\sqrt{5}}\right )∪\left (\displaystyle \frac{1}{5\sqrt{5}};2\right ]\)
16. В июле 2026 года планируется взять кредит на целое число миллионов рублей на пять лет. Условия его возврата таковы:
- каждый январь долг возрастает на 16% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
- в июле 2027, 2028 и 2029 годов долг остаётся равным первоначальному;
- выплаты в 2030 и 2031 годах равны;
- к июлю 2031 года долг должен быть выплачен полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат заёмщика будет меньше 9 млн рублей.
Решение:
Пусть \(S\) – сумма кредита, \(k=1,16\) повышающий коэффициент банка.
После первого, второго и третьего начисления процентов долг увеличивается в \(k\) раз и становится равен \(Sk\);
После 1-й, 2-й и 3-й выплаты долг равен \(S\). Значит, первая, вторая и третья выплаты равны \(S(k-1)\).
После 4-го начисления процентов долг равен \(Sk\),
После 4-й выплаты уменьшается на \(x\) и равен \(Sk-x\).
После 5-го начисления процентов и 5-й выплаты сумма долга
\((Sk-x)\cdot k-x=0\);
\(Sk^{2}-x(k+1)=0\);
\(x=\displaystyle \frac{Sk^{2}}{k+1}\).
Общая сумма выплат равна \(B=3S(k-1)+2x=3S(k-1)+2\cdot\displaystyle \frac{Sk^{2}}{k+1} < 9.\)
Будем вести расчеты в млн. рублей:
\(S(3(k-1)+\displaystyle \frac{2k^{2}}{k+1} < 9\);
\(S\cdot\displaystyle \frac{3(k-1)(k+1)+2k^{2}}{k+1} < 9\);
\(S\cdot\displaystyle \frac{5k^{2}-3}{k+1} < 9\);
\(S\cdot\displaystyle \frac{5\cdot1,16^{2}-3}{1,16+1} < 9\);
\(S < \displaystyle \frac{9\cdot2,16}{3,728}=\displaystyle \frac{9\cdot2160}{3728}\);
\(S < \displaystyle \frac{9\cdot540}{932}; \ S < \frac{9\cdot135}{233}\);
\(S < \displaystyle \frac{1215}{233}; \ S < 5 \frac{50}{233}\);
\(S≤5\);
\(S_{max}=5\).
17. Точки \(P, \ Q, \ W\) делят стороны выпуклого четырёхугольника \(ABCD\) в отношении \(AP:PB=CQ:QB=CW:WD=2:5\). В треугольнике \(PQW\) угол \(W\) острый, при этом радиус описанной около этого треугольника окружности равен \(\displaystyle \frac{17}{4}, \ PQ=\frac{15}{2}, \ QW=4\).
а) Докажите, что треугольник \(PQW\) прямоугольный.
б) Найдите площадь четырёхугольника \(ABCD\).
Решение:
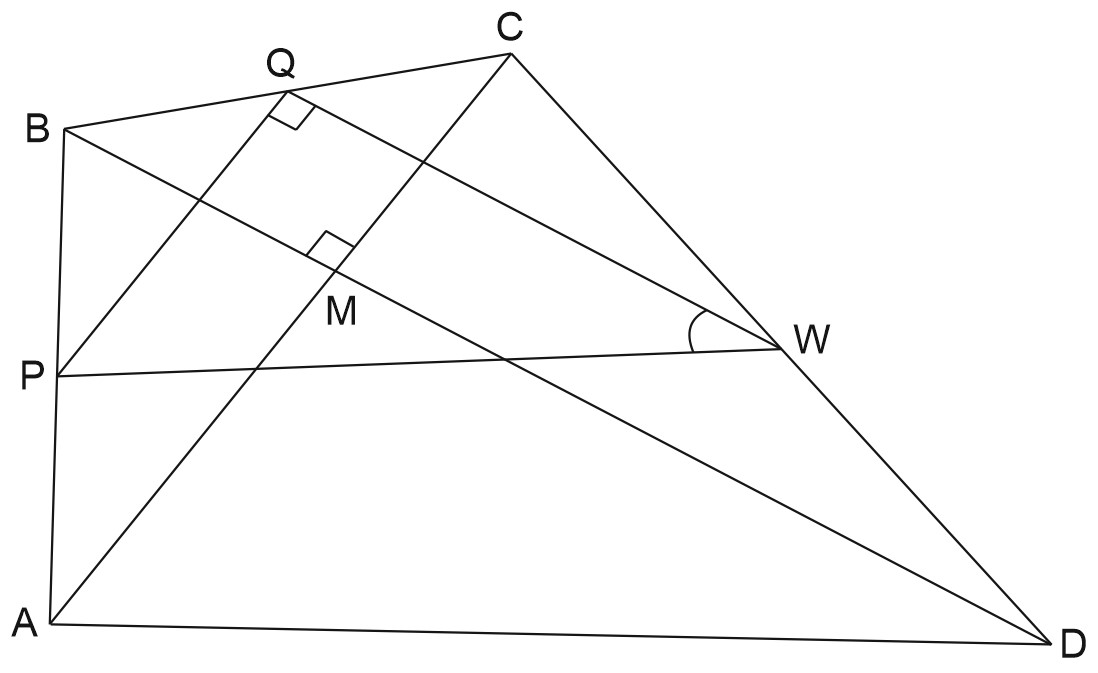
\(R_{∆PQW}=\displaystyle \frac{17}{4}\);
\(PQ=\displaystyle \frac{15}{2}\);
\(QW=4\).
а) Докажем, что \(∆PQW\) - прямоугольный.
\(2R=\displaystyle \frac{PQ}{sin∠PWQ} = \frac{QW}{sin∠QPW} ⇒sin∠PWQ=\displaystyle \frac{PQ}{2R}=\frac{15}{17}\);
\(sin∠QPW=\displaystyle \frac{QW}{2R}=\frac{8}{17}\);
\(sin^{2}∠PWQ+sin^{2}∠QPW=\left (\displaystyle \frac{15}{17}\right )^{2}+ \left (\displaystyle \frac{8}{17}\right )^{2}=1\);
\(∠PWQ\) острый \(⇒sin∠QPW=cos∠PWQ\);
\(∠PWQ+∠QPW=90^{\circ}⇒∠PQW=90^{\circ}\).
б) Найдем площадь четырёхугольника \(ABCD\).
\(∆ABC ∼∆PBQ; \ AB:PB=BC:BQ=7:5\).
Тогда \(AC=\displaystyle \frac{7}{5}PQ=\displaystyle \frac{21}{2}.\)
Аналогично, \(∆BCD ∼∆QCW;, \ BC:QC=CD:CW=7:2,\)
\(BD=\displaystyle \frac{7}{2}QW=14,\)
\( PQ||AC, \ OW||BD,\)
\(S_ABCD=\displaystyle \frac{1}{2}\cdot AC \cdot BD=\frac{147}{2}=73,5\).
18. Найдите все значения \(a\), при каждом из которых неравенство \(|x+2a+8|+|x-2a-16|≤3|x|+3|x-4|\) выполняется при всех значениях \(x\).
Решение:
Замена: \(x-4=z\), тогда \(x=z+4\).
\(|z+2a+12|+|z-2a-12|≤3|z+4|+3|z|\).
Замена: \(2a+12=b\);
\(|z+b|+|z-b|≤3(|z+4|+|z|)\) (*).
Построим график функции \(f(z)=3(|z+4|+|z|)\):
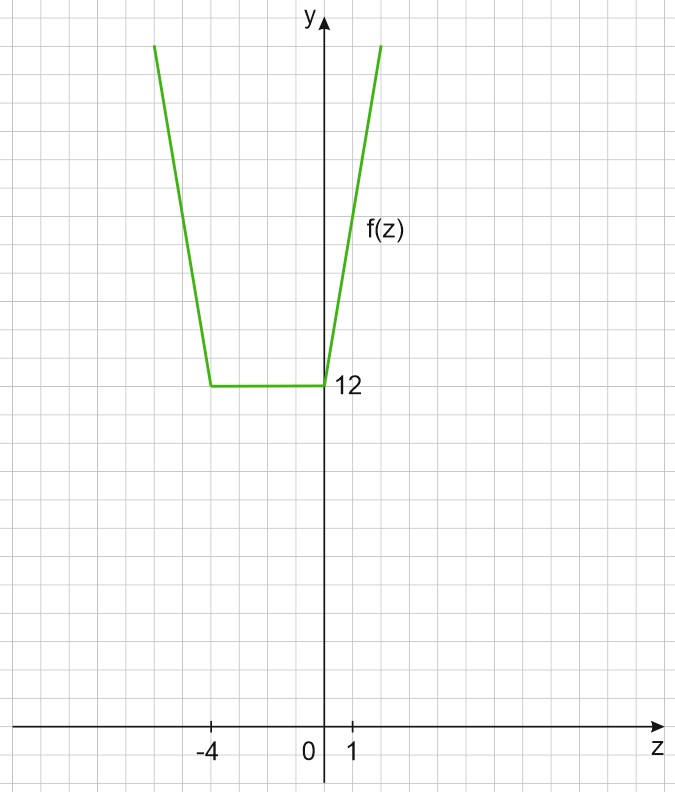
Если \(z≤-4, \ f(z)=-6z-12\);
если \(-4 < z < 0, \ f(z)=12\);
если \(z≥0, \ f(z)=6z+12\).
Построим график функции \(g(z)=|z+b|+|z-b|)\).
Уравнение (*) четно относительно \(b\); если \(b_0\) – решение, то \(-b_0\) тоже решение.
Если \(b=0\), то \(g(z)=|z|\).
Если \(b≥0\), то:
при \(z < -b, \ g(z)=-2z\),
при \(-b≤z≤b, \ g(z)=2b\),
при \(z > b, \ g(z)=2z\).
График функции \(g(z)\) состоит из луча с угловым коэффициентом -2 с началом в точке \((-b; 2b)\); горизонтального участка \(y=2b\) и луча с угловым коэффициентом 2 и началом в точке \((b; 2b)\).
Исходное неравенство выполняется при всех \(z\), если график \(g(z)\) лежит не выше графика \(f(z)\) при всех \(z\).
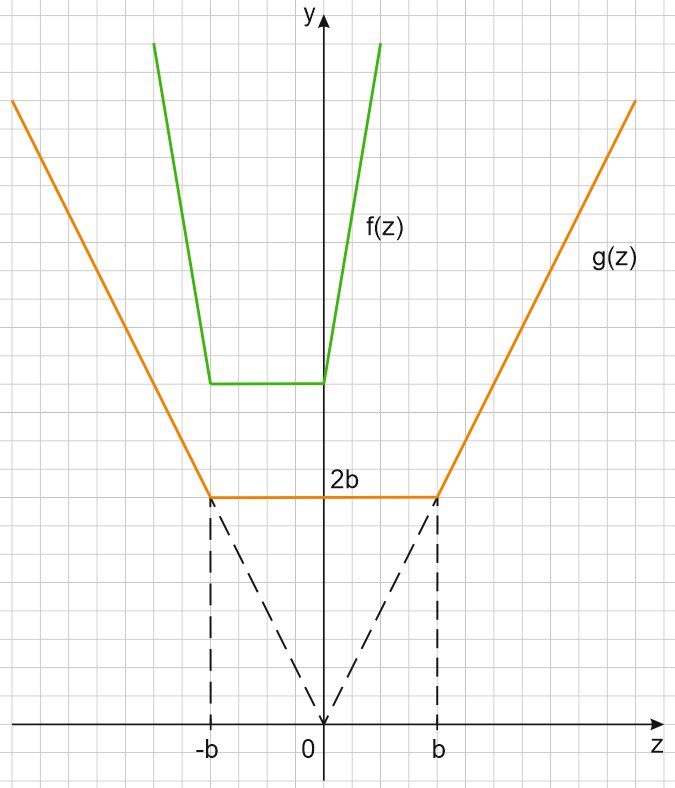
Наклонные участки графиков \(f(z)\) и \(g(z)\) не имеют общих точек. Неравенство выполнено, если горизонтальный участок функции \(g(z)\) лежит не выше горизонтального участка \(f(z)\), то есть \(2b≤12\) при \(b≥0\).
Так как уравнение (*) четно относительно \(b\),
\(2|b|≤12\);
\(|b|≤6\);
\(-6≤b≤6; \ b=2a+12\);
\(-6≤2a+12≤6\);
\(-3≤a+6≤3\);
\(-9≤a≤-3\).
Это ответ.
19. На доске написано 10 различных натуральных чисел. Среднее арифметическое шести наименьших из них равно 4, а среднее арифметическое шести наибольших равно 12.
а) Может ли наименьшее из этих десяти чисел равняться 2?
б) Может ли среднее арифметическое всех десяти чисел равняться 9?
в) Найдите наибольшее значение среднего арифметического всех десяти чисел.
Решение:
На доске 10 чисел. Расставим их по порядку: \(x_1 < x_2 < x_3 < ⋯x_{10}\)
Перейдем от средних арифметических к суммам чисел.
\(x_1+x_2+x_3+x_4+x_5+x_6=4\cdot6=24\);
\(x_5+x_6+x_7+x_8+x_9+x_{10}=12\cdot6=72\).
а) Если \(x_1=2\), то \(x_2≥3, \ x_3≥4, \ x_4≥5, \ x_5≥6, \ x_6≥7\).
Тогда \(x_1+x_2+⋯+x_6≥2+3+4+5+6+7=27 > 24\), противоречие.
Ответ: Нет, не может.
б) В этом случае сумма всех чисел равна \(90=9\cdot10\).
Так как \(x_5+x_6+⋯+x_{10}=72\),
\(x_1+x_2+x_3+x_4=18\), при этом
\(x_1+x_2+x_3+x_4+x_5+x_6=24\), значит \(x_5+x_6=6\).
Так как \(x_5 < x_6, \ x_5≤2\).
Тогда \(x_4≤1, \ x_3 < 1\) – противоречие.
Нет, не может.
в) Обозначим сумму всех чисел \(S\), найдем \(S_{max}\), тогда наибольшее среднее арифметическое равно \(\displaystyle \frac{S_{max}}{10}\).
Сумма первых 6 чисел равна \(x_1+x_2+x_3+x_4+x_5+x_6=24\).
Если \(x_1≥2,\) то \(x_2≥3, \ x_3≥4, \ x_4≥5…\)
\(x_1+x_2+x_3+x_4+x_5+x_6≥2+3+4+5+6+7=27 > 24;\) значит, \(x_1=1\).
Если \(x_2≥3,\) то \(x_1+x_2+x_3+x_4+x_5+x_6≥1+3+4+5+6+7=26 > 24;\) значит, \(x_2=2\).
Если \(x_3≥4,\) то \(x_1+x_2+x_3+x_4+x_5+x_6≥1+2+4+5+6+7=25 > 24;\) значит, \(x_3=3\).
Тогда \(x_1+x_2+x_3=6\);
\(x_4+x_5+x_6=24-6=18\);
\(x_4 < x_5 < x_6\).
Возможны варианты:
1) \(x_4=5; \ x_5=6; \ x_6=7;\)
2) \(x_4=4; \ x_5=6; \ x_6=8;\)
3) \(x_4=4; \ x_5=5; \ x_6=9;\)
Так как \(x_5+x_6+x_7+x_8+x_9+x_{10}=72\).
Выберем вариант с наибольшим возможным \(x_4=5\).
Тогда сумма всех чисел равна \(1+2+3+5+72=83\); наибольшее среднее арифметическое равно 8,3.
Приведем пример: \(1, \ 2, \ 3, \ 5, \ 6, \ 7, \ 8, \ 9, \ 10, \ 32\).
Тогда \(\displaystyle \frac{1+2+3+5+6+7}{6}=4\);
\(\displaystyle \frac{6+7+8+9+10+32}{6}=12\).
Среднее арифметическое всех чисел равно 8,3.






























