В вариантах ОГЭ и ЕГЭ вам также встретятся задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.
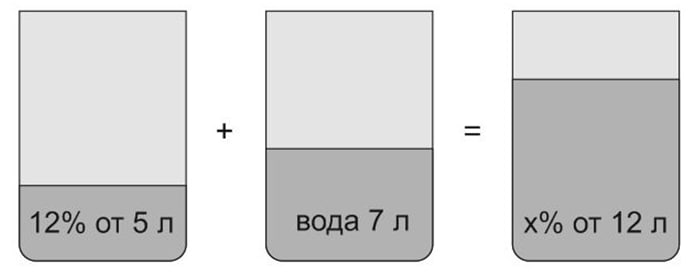
1. В сосуд, содержащий \(5\) литров \(12\)-процентного водного раствора некоторого вещества, добавили \(7\) литров воды. Сколько процентов составляет концентрация получившегося раствора?
В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим \(x\).
Первый сосуд содержал \(0,12 \cdot 5=0,6\) литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
\(0,12 \cdot 5=\genfrac{}{}{}{0}{\displaystyle x}{\displaystyle 100} \cdot 12;\)
\(x=5.\)
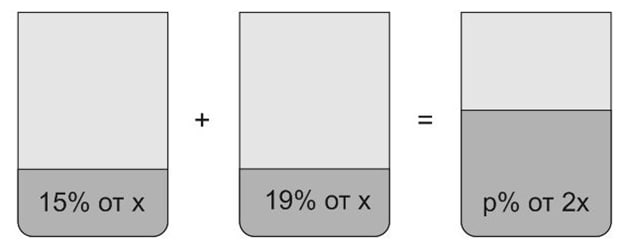
2. Смешали некоторое количество \(15\)-процентного раствора некоторого вещества с таким же количеством \(19\)-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть масса первого раствора равна \(x\). Масса второго — тоже \(x\). В результате получили раствор массой \(2x\). Рисуем картинку.
Получаем: \(0,15x+0,19x=0,34x=0,17\cdot 2x.\)
Ответ: \(17.\)
3. Виноград содержит \(90\%\) влаги, а изюм — \(5\%\). Сколько килограммов винограда требуется для получения \(20\) килограммов изюма?
Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы.
Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка.
Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось \(90\%\) воды, значит, «сухого вещества» было \(10\%\). В изюме \(5\%\) воды и \(95\%\) «сухого вещества». Пусть из \(x\) кг винограда получилось \(20\) кг изюма. Тогда
\(10\%\) от \(x=95\%\) от \(20.\)
Составим уравнение:
\(0,1x=0,95\cdot20\)
и найдем \(x\).
Ответ: \(190.\)
Запишем правила решения задач на сплавы, смеси и растворы в одну табличку:
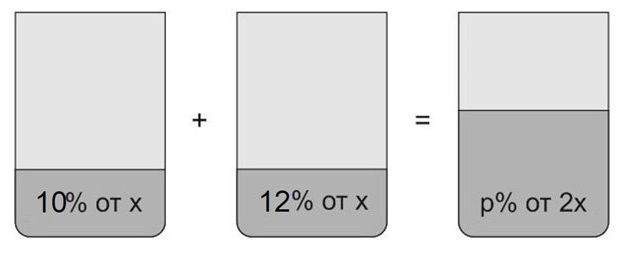
4. Смешали некоторое количество 10-процентного раствора некоторого вещества с таким же количеством 12-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
Пусть масса первого раствора равна \(x\). Масса второго – тоже \(x\). В результате получили раствор массой \(2x\). Рисуем картинку.
Масса вещества в первом растворе равна 10% от \(x\), то есть \(0,1x\). Масса вещества во втором растворе \(0,12x\).
Получаем: \(0,10x+0,12x=0,22x.\)
Масса вещества в третьем растворе составляет \(p\)% от \(2x\), то есть равна \(\frac{p}{100}\cdot 2x\).
Получим: \(0,22x=\frac{p}{100}\cdot 2x.\)
Отсюда \( x=11.\)
Ответ: 11.
5. В сосуд, содержащий 6 литров 11-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение:
В таких задачах слова «11-процентный раствор» означают «раствор, в котором вещество занимает 11% объема».
Составим таблицу:
| I раствор | Вода | II раствор | |
| Объем раствора, л | \(6\) | \(5\) | \(5+6=11\) |
| Объем растворенного вещества, л | \(0,11\cdot 6=0,66\) | \(0\) | \(0,66+0=0,66\) |
Пусть концентрация полученного раствора равна \(x\), тогда
\(11x=0,66.\)
\(x=0,06\). Значит, концентрация вещества в растворе была равна 6%.
Ответ: 6.
6. Содержание сахара в одном соке – 10%, а в другом – 15%. Смешали 4л первого и 6 л второго сока. Каково содержание сахара (в процентах) в смеси?
Решение:
Всего сахара в смеси: \(0,1\cdot 4+0,15\cdot 6=1,3\) л. В процентах \(\frac{1,3}{10}\cdot 100\)%=\(13\)%.
Ответ: 13.
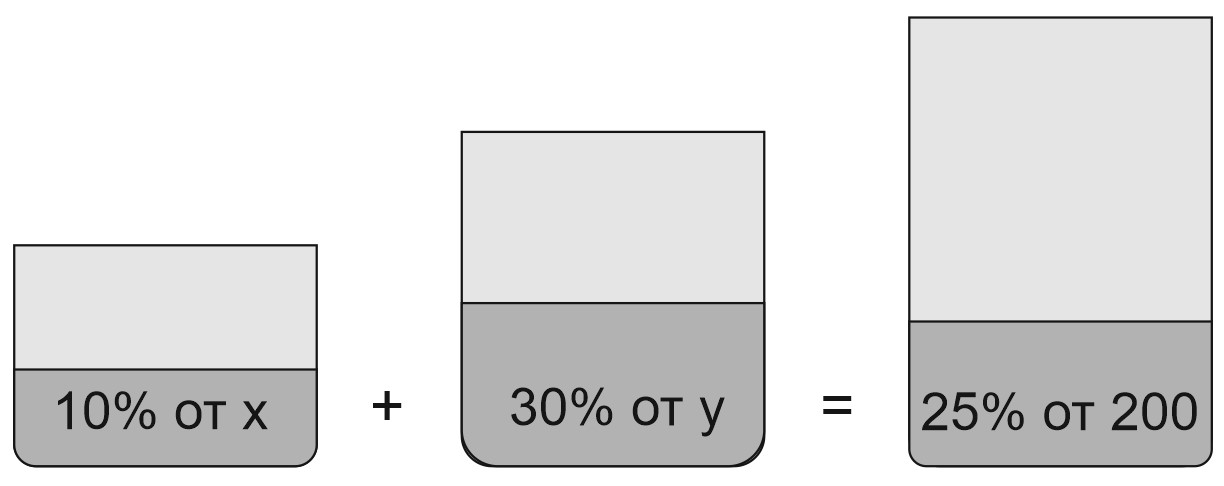
7. Имеется два сплава. Первый сплав содержит \(10\%\) никеля, второй — \(30\%\) никеля. Из этих двух сплавов получили третий сплав массой \(200\) кг, содержащий \(25\%\) никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть масса первого сплава равна \(x\), а масса второго равна \(y\). В результате получили сплав массой \(x+y=200\).
Запишем простую систему уравнений:
\(\left\{\begin{matrix}x+y=200,
\\ 0,1x+0,3y=0,25 \cdot200.
\end{matrix}\right.\)
Первое уравнение — масса получившегося сплава, второе — масса никеля.
Решая, получим, что \(x=50, y=150\).
Ответ: \(100\).
8. Смешав \(30\)-процентный и \(60\)-процентный растворы кислоты и добавив \(10\) кг чистой воды, получили \(36\)-процентный раствор кислоты. Если бы вместо \(10\) кг воды добавили \(10\) кг \(50\)-процентного раствора той же кислоты, то получили бы \(41\)-процентный раствор кислоты. Сколько килограммов \(30\)-процентного раствора использовали для получения смеси?
Пусть масса первого раствора \(x\), масса второго равна \(y\). Масса получившегося раствора равна \(x+y+10\). Запишем два уравнения, для количества кислоты.
\(\left\{\begin{matrix}0,3x + 0,6y = 0,36 \left(x + y + 10\right),
\\ 0,3x + 0,6y + 0,5 \cdot 10 = 0,41 \left(x + y + 10\right).
\end{matrix}\right.\)
Решаем получившуюся систему. Сразу умножим обе части уравнений на \(100\), поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.
\(\left\{\begin{matrix}30x + 60y = 36x + 36y + 360,
\\ 30x + 60y + 500 = 41x + 41y + 410;
\end{matrix}\right.\)
\(\left\{\begin{matrix}4y - x = 60,
\\ 11x - 19y = 90;
\end{matrix}\right.\)
\(x=60, y=30.\)
Ответ: \(60\).