В задачах на построение сечений мы применяем все те определения, теоремы, свойства и признаки, которые изучаем и доказываем на уроках в школе.
Например, если две плоскости имеют общую точку, то они пересекаются по прямой. Это значит, что плоскость сечения и, например, плоскость грани пирамиды будут пересекаться по прямой, и на чертеже будет показана часть этой прямой – отрезок.
Как вы думаете - может ли восьмиугольник быть сечением куба?
И может ли правильный пятиугольник быть сечением куба?
Чтобы соединить какие-либо две точки на чертеже, нам нужна плоскость, в которой эти точки лежат. Иногда это грань объемного тела. Иногда – вспомогательная плоскость.
А вообще сечение - это плоская фигура, которая образуется при пересечении объемного тела плоскостью и граница которой лежит на поверхности этого объемного тела.
Конечно, восьмиугольник сечением куба быть не может. Ведь у куба 6 граней, и поэтому сечение куба не может иметь больше 6 сторон.
При построении сечений мы часто используем следующие теоремы:
1. Линии пересечения параллельных плоскостей третьей плоскостью параллельны.
Именно поэтому правильный пятиугольник не может быть сечением куба. Ведь 4 из 5 сторон этого пятиугольника лежат в параллельных гранях куба и поэтому параллельны. А у правильного пятиугольника параллельных сторон нет.
2. Теорема о прямой и параллельной ей плоскости:
Пусть прямая \(m\) параллельна плоскости \(\alpha\). Если плоскость \(\beta \) проходит через прямую \(m\) и пересекает плоскость \(\alpha\) по прямой \(c\), то \(c\) параллельна \(m\).
Эта теорема помогает, например, при построении сечений пирамиды.
Разберем несколько задач на построение сечений.
1. Постройте сечение тетраэдра плоскостью, проходящей через точки \(M, \; N, \; K.\) Точка \(M\) лежит на ребре \(AD, \; N\) — на ребре \(DC, \; K\) — на ребре \(AB\).
Решение:
Проведем \(MK\) в плоскости грани \(ABD\) и \(MN\) в плоскости грани \(ADC\).
Продлим отрезки \(MN\) и \(AC\); \((MN)\cap (AC)=P; \; P\in \left(ABC\right).\)
Проведем \(PK\) в плоскости нижней грани; \(PK\cap BC=L;\) четырехугольник \(MNLK\) — искомое сечение.
2. Постройте сечение тетраэдра плоскостью, проходящей через точки \(M, \; N, \; K.\) Точка \(N\) лежит на ребре \(BC, \; M \in AD, \; K \in BD, \; MK \parallel AB. \)
Решение:
Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой \(NT\), параллельной \(MK\).
Прямая \(MK\) параллельна \(AB\), лежащей в плоскости основания \(ABC\). Значит, \(MK \parallel (ABC).\)
Плоскость сечения проходит прямую \(MK\), параллельную плоскости \(ABC\). По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости \(ABC\) параллельна прямой \(MK\). Трапеция \(MKNT\) — искомое сечение.
3. Постройте сечение куба \(A\dots D_1\), проходящее через вершину \(D_1\) и середины ребер \(AB\) и \(BC\).
Решение:
Пусть \(M\) — середина \(AB, \; N\) — середина \(BC, \; MN\in \left(ABC\right).\) Продолжим прямую \(MN\) до пересечения с продолжениями ребер \(DC\) и \(AD\);
\(\left(MN\right)\cap \left(DC\right)=K. \; \left(MN\right)\cap \left(AD\right)=P. \)
Треугольники \(AMP\) и \(KCN\) — прямоугольные равнобедренные, причем \(AP = CK = \displaystyle \frac{AB}{2}.\)
Проведем \(D_1K\) — в плоскости задней грани и \(D_1P\) — в плоскости левой грани куба;
\(D_1K\cap {CC}_1=F, \; {D}_1P\cap AA_1=T.\)
Пятиугольник \(MNFD_{1}T\) — искомое сечение. В нем есть параллельные стороны: \(TM\parallel D_1F, \; TD_1\parallel NF\), так как линии пересечения параллельных плоскостей третьей плоскостью параллельны.
4. Постройте сечение куба \(A\dots D_{1}\), проходящее через вершину \(B\) и середины ребер \(AA_1\) и \(CC_1.\)
Решение:
Пусть \(M\) — середина ребра \(AA{}_{1}, \; N\) — середина ребра \(CC_{1}.\)
Поскольку линии пересечения параллельных плоскостей третьей плоскостью параллельны, плоскость сечения пересекает заднюю грань по прямой, параллельной \(BM\), а левую грань — по прямой, параллельной \(BM\). Тогда искомое сечение — ромб \(BND{}_{1}M.\)
5. Постройте сечение правильного тетраэдра \(ABCS\), проходящее через точку \(K\) — середину ребра \(AB\), точку \(M\), делящую ребро \(AS\) в отношении \(SM:AM = 1:2\), и точку \(N\) — середину апофемы грани \(SBC\).
Решение:
Пусть \(SH\) — апофема грани \(SBC; \; N\)—середина \(SH.\)
Проведем \(MN\) в плоскости \(ASH;\)
\(\left(MN\right)\cap \left(AH\right)=P; \; P\in \left(ABC\right).\)
\(KP\cap BC=F; \; FN\cap SC=E.\)
Четырехугольник \(KMEF\) — искомое сечение.
6. Постройте сечение правильного тетраэдра \(ABCS\), проходящее через точку \(K\) — середину ребра \(AB\), и точки \(M\) и \(T\) — центры граней \(ASC\) и \(SBC\).
Пусть \(SE\) и \(SH\) — апофемы граней \(ASC\) и \(SBC\); точки \(M\) и \(T\) делят отрезки \(SE\) и \(SH\) в отношении \(2:1\), считая от точки \(S\).
Из подобия треугольников\(SMT\) и \(SEH\) получим, что \(MT\parallel EH.\) Значит, \(MT\parallel (ABC).\)
По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и нижней грани параллельна прямой \(MT\). Это значит, что плоскость сечения пересекает грань \(ABC\) по прямой \(AB\). Достроим сечение.
\(\left(BT\right)\cap \left(SC\right)=F,\) где \(F\) — середина \(SC\);
\(\left(AM\right)\cap \left(SC\right)=F; \; \triangle ABF\) — искомое сечение.
7. Постройте сечение куба \(A\dots D_1\), проходящее через точку \(M\), лежащую на ребре \(DD_1\) и точки \(T\) и \(K\), принадлежащие граням \(ABC\) и \(DCC_{1}\).
Решение:
Точки \(M\) и \(K\) лежат в плоскости задней грани \(DCC{}_{1}D{}_{1}\). Соединив \(M\) и \(K\), получим, что
\(MK\cap CC{}_{1}=E, \; (MK)\cap (DC)=P.\)
Соединив точки \(P\) и \(T\) в нижней грани, получим \(FN\) — линию пересечения плоскости сечения с нижней гранью;
\(F\in AD, \; N\in BC\). Трапеция \(FMEN\) — искомое сечение.
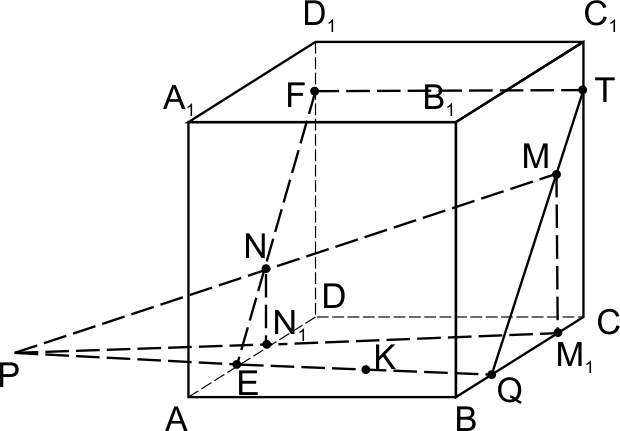
8. И самый сложный случай. Построим сечение куба \(A\dots D_1\) плоскостью \(MNK\), где \(M \in \left(BB_1C_1\right), \; N\in \left(AA_1D_1\right), \; K\in \left(ABC\right)\), причем расстояния от точек \(M\) и \(N\) до плоскости \(ABC\) различны.
Решение:
Пусть точки \(M{}_{1}\) и \(N{}_{1}\) — проекции точек \(M\) и \(N\) на плоскость нижней грани.
Плоскость \((MNN{}_{1})\) проходит через параллельные прямые \(MM{}_{1}\) и \(NN{}_{1}\).
Проведем в этой плоскости \(MN\) и \(M{}_{1}N{}_{1};\)
\((MN )\cap ( M{}_{1}N{}_{1})=P\).
Точки \(P\) и \(K\) лежат в нижней грани куба, следовательно, плоскость сечения пересекает нижнюю грань по прямой \(PK\). Дальнейшее построение — очевидно.