1. При каких значениях параметра \(a\) система \(
\begin{cases}
2^x+2^{\frac{4}{x}}=(a^2-4)^2+y^2+8, \\
|y|\cdot z^4+2z^2-a^2z+a+4=0
\end{cases}\ \) имеет единственное решение \((x_0,y_0,z_0)\)?
Решение:
В этой системе три переменных и всего 2 уравнения.
1) Уравнения системы четны относительно \(y\), и если тройка чисел \((x_0,y_0,z_0)\) — решение, то и тройка \((x_0,-y_0,z_0)\) — тоже решение. Вместе с каждым решением \((x_0,y_0,z_0)\) возникает также решение \((x_0,-y_0,z_0)\). Единственное решение может быть, только если \(y=0\). Это одно из необходимых условий.
Мы воспользовались четностью уравнений системы относительно \(y\).
2) В первом уравнении системы \((a^2-4)^2+y^2+8 \geqslant 8 \) — левая часть.
Значит, и правая его часть не меньше \(8, \ 2^x+2^{\frac{4}{x}} \geqslant 8. \)
Покажем, что условие \(2^x+2^{\frac{4}{x}} \geqslant 8 \) выполняется только при \(x>0.\)
ОДЗ этого неравенства: \(x\neq 0.\)
Если \(x>0,\) то \(2^x<1\) и \(2^{\frac{4}{x}}<1; \) тогда \(2^x+2^{\frac{4}{x}} < 2 < 8. \) Значит, \(x>0.\)
Заметим, что при \(x>0\) функция \(f(x)=2^x+2^{\frac{4}{x}}\) принимает одинаковые значения при \(x=x_0\) и \(x=\displaystyle \frac{4}{x_0}. \)
Тогда уравнение \(2^x+2^{\frac{4}{x}} =c\) имеет два решения, причем оба положительны.
Уравнение \(2^x+2^{\frac{4}{x}} =c\) может иметь единственное положительное решение, если \(x=\displaystyle \frac{4}{x}\) (воспользовались методом симметрии).
Это значит, что \(x^2=4.\) Положительное решение этого уравнения: \(x=2.\)
Если \(x=2,\) то \(2^x+2^{\frac{4}{x}} =8,\) и система может иметь единственное решение. Мы нашли второе необходимое условие.
Получается, что исходная система может иметь единственное решение, если это решение вида \((2; 0; z). \)
Подставим \(x = 2\) и \(y = 0\) в первое уравнение: \(2^x+2^{\frac{4}{x}}=(a^2-4)^2+y^2+8.\)
\(8=(a^2-4)^2+8; \ (a^2-4)^2=0, \ a^2=4,\) тогда \(a=2\) или \(a=-2.\)
Теперь второе уравнение исходной системы.
Если \(y=0,\) оно выглядит так: \(2z^2-a^2z+a+4=0.\)
Это квадратное уравнение относительно \(z\); оно имеет единственное решение, если \(D=0.\)
\(D=a^4-8(a+4)=0.\)
Подставив \(a=2,\) получим: \(16-8\cdot6<0, \ a=2\) не подходит.
Подставив \(a=-2,\) получим \(16-8\cdot2=0. \ \) Тогда \(z=\displaystyle \frac{4}{4}=1.\)
Покажем, что при \(a=-2\) нет других решений, кроме тройки чисел \((2;0;1).\)
Подставим \(a=-2\) в исходную систему.
\( \begin{cases}
2^x+2^{\frac{4}{x}}=y^2+8, \\
|y|\cdot z^4+2z^2-4z+2=0.
\end{cases} \)
Второе уравнение: \(|y|\cdot z^4+2(z-1)^2=0.\)
Оба слагаемые неотрицательны, значит, \(|y|\cdot z^4=0\) и \((z-1)^2=0.\)
Тогда \(z=1, \ y=0,\) из первого уравнения \(x=2,\) система имеет единственное решение.
Ответ: \(a = - 2.\)
2. Найдите все значения \(a\), при каждом из которых система \(\left\{\begin{matrix} 3\left | x-2a \right |+2\left | y-a \right |=6,\\xy-x-2y+2=0 \end{matrix}\right.\) имеет ровно три различных решения.
Решение:
\(\left\{\begin{matrix} 3|x-2a|+2|y-a|=6, \\xy-x-2y+2=0; \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 3|x-2a|+2|y-a|=6,\\(x-2)(y-1)=0; \end{matrix}\right. \Leftrightarrow\left\{\begin{matrix} 3|x-2a|+2|y-a|=6, \\ \left[ \begin{array}{ccc} x=2,\\ y=1 .\\ \end{array} \right. \end{matrix}\right.\)
Мы разложили второе уравнение на множители: \(xy-x-2y+2=x(y-1)-2(y-1)=(x-2)(y-1).\)
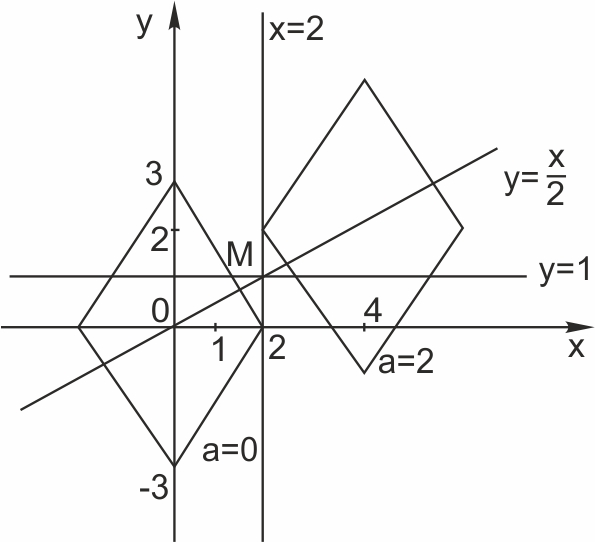
Первое уравнение системы задаёт ромб с диагоналями, параллельными осям координат; горизонтальная диагональ равна 4, вертикальная диагональ равна 6.
Центр ромба находится в точке \(p(2a;a)\), то есть лежит на прямой \(y=\displaystyle \frac{x}{2}.\)
Мы нашли координаты центра ромба, сказав, что \(x_p =2a, \ y_p =a,\) отсюда \(y_p = \displaystyle \frac{x_p}{2}.\)
Система имеет ровно 3 различных решения, если ромб, заданный первым уравнением, имеет ровно 3 общие точки с совокупностью прямых
\(\left[\begin{array}{ccc}
x=2 ,\\
y=1.\\
\end{array}
\right.\)
Это происходит в следующих случаях:
1) Прямая \(x=2\) проходит через одну из вершин ромба. Это происходит, если \(a=0\) или \(a=2.\)
В этом случае расстояние от центра ромба до прямой \(x=2\) равно 2.
2) Случай, когда расстояние от центра ромба до прямой \(y=1\) равно 3, не подходит. В этом случае ромб не имеет общих точек с прямой \(x=2.\)
3) Случай, когда точка \(M\) пересечения прямых \(y=1\) и \(x=2\) лежит на одной из сторон ромба.
Это значит, что координаты точки \(M \ x_M=2\) и \(y_M=1\) — удовлетворяют уравнению, задающему ромб. Подставив их в уравнение, получим:
\(3|2-2a|+2|1-a|=6;\)
\(6|a-1|+2|a-1|=6;\)
\(|a-1|=\displaystyle \frac{3}{4};\)
\(a=\displaystyle \frac{1}{4}\) или \(a=\displaystyle \frac{7}{4}.\)
Ответ: \( 0; \ \displaystyle \frac{1}{4}; \ \displaystyle \frac{7}{4}; 2.\)
3. При каких значениях параметра \(a\) система \(\left\{\begin{matrix} 2cos x+asin y=1 ,\\ log_{z}siny=log_{z}a\cdot log_a\left ( 2-3cos x \right ),\\ log_{a}z+log_{a}\left ( \displaystyle \frac{1}{2a}-1 \right )=0 \end{matrix}\right. \ \) имеет хотя бы одно решение?
Решение:
Выпишем ОДЗ системы:
\(\left\{\begin{matrix} sin y > 0, \\ a > 0 ,\: a\ne1, \\ 2-3cosx > 0, \\ z > 0,\: z\ne1, \\ \displaystyle \frac{1}{2a}-1 > 0; \end{matrix}\right. \: \left\{\begin{matrix} sinx > 0, \\ 0 < a < \displaystyle \frac{1}{2} ,\\2-3cos x > 0 , \\ z > 0,\: z\ne1. \end{matrix}\right.\)
При выполнении этих условий преобразуем уравнение исходной системы:
\(\left\{\begin{matrix} 2cos x+a sin y=1,\\ \displaystyle \frac{log_z sin y}{log_z a}=log_a (2-3cos x) ,\\ log_a\left (z\cdot \left (\displaystyle \frac{1}{2a}-1\right )\right )=0. \end{matrix}\right.\)
Во втором уравнении применим формулу перехода к другому основанию:
\(\displaystyle \frac{log_c b}{log_c a}=log_a b;\)
\(log_a sin y=log_a(2-3cos x);\)
\(sin y=2-3cos y.\)
В уравнении 3 представим 0 как \(log_a 1.\)
Получим: \(z\left (\displaystyle \frac{1}{2a}-1\right )=1.\)
С учётом ОДЗ система примет вид:
\(\left\{\begin{matrix} sin y > 0, \\ 0 < a < \displaystyle \frac{1}{2}, \\2-3cos x > 0, \\siny=2-3cos x ,\\2cosx+asin y=1, \: \: \: \:\: (*) \\z > 0, \, z\ne1, \\z\left (\displaystyle \frac{1}{2a}-1\right )=1. \end{matrix}\right.\)
Подставим \(sin\, y=2-3cosx\) в уравнение (*). Получим:
\(2cosx+2a-3 a \, cosx=1.\)
Отсюда \(cosx=\displaystyle \frac{2a-1}{3a-2}=\frac{1-2a}{2-3a}.\)
Из условия \(2-3cosx > 0\) имеем: \(cosx < \displaystyle \frac{2}{3}.\)
Так как \(cos\, x \in [-1;1]\), имеем: \(-1 \leq \displaystyle \frac{2a-1}{3a-2} < \displaystyle \frac{2}{3};\)
\(\left\{\begin{matrix} \displaystyle \frac{2a-1}{3a-2}\geq-1, \\\displaystyle \frac{2a-1}{3a-2} < \frac{2}{3}. \end{matrix}\right.\)
При \(0 < a < \displaystyle \frac{1}{2}\) оба неравенства выполняются.
Рассмотрим также условие \(0 < siny \leq 1.\)
Из уравнения \(siny=2-3cosx\) имеем:
\(sin y =2-3 \cdot \displaystyle \frac{2a-1}{3a-2}=\frac{6a-4-6a+3}{3a-2}=-\displaystyle \frac{1}{3a-2}=\frac{1}{2-3a}.\)
Условие \(2-3a > \) выполнено при \(0 < a < \displaystyle \frac{1}{2}.\)
Проверим: \(\displaystyle \frac{1}{2-3a} \leq 1:\)
\(1 \leq 2-3a; \, 3a \leq 1; \, a \leq \displaystyle \frac{1}{3}.\)
Значит, \(0 < a\leq \displaystyle \frac{1}{3}.\)
Осталось условие \(z\ne1.\)
Из уравнения \(z\left (\displaystyle \frac{1}{2a}-1\right )=1.\)
Получим: \(z \cdot \displaystyle \frac{1-2a}{2a}=1,\)
\(z= \displaystyle \frac{2a}{1-2a} \ne 1; \, a \ne \displaystyle \frac{1}{4}.\)
Ответ: \(a \in \left (0; \displaystyle \frac{1}{4}\right ) \cup \left (\displaystyle \frac{1}{4}; \frac{1}{3}\right ].\)
4. Дана четырёхугольная пирамида \(SABCD\) с прямоугольником \(ABCD\) в основании. Сторона \(AB\) равна 4, а \(BC\) равна \(4 \sqrt{2}.\) Вершина пирамиды \(S\) проецируется в точку пересечения диагоналей прямоугольника. Из вершины \(A\) и \(C\) на ребро \(SB\) опущены перпендикуляры \(AP\) и \(CQ.\)
а) Докажите, что точка \(P\) является серединой отрезка \(BQ.\)
б) Найдите угол между плоскостями \(SBA\) и \(SBC\), если ребро \(SD\) равно 8.
Решение:
а) Покажем, что \(O\) – середина \(BQ.\)
Поскольку \(ABCD\) – прямоугольник, его диагонали равны, \(AC=BD.\)
Точка \(O\) – точка пересечения диагоналей прямоугольника \(ABCD, \ AO=OC=OB=OD,\) тогда \(SA=SB=SC=SD.\) Наша пирамида не является правильной, но все ее боковые ребра равны.
Значит, треугольники \(ASB\) и \(BSC\) – равнобедренные.
Пусть \(b\) – боковое ребро пирамиды.
Заметим, что \(\triangle APB \sim \triangle SHB\), где \(SH\) - апофема боковой грани.
\(cos \varphi = cos \angle SBA;\)
\(\displaystyle \frac{PB}{AB} = \frac{AB}{2\cdot b}.\)
Тогда \(PB=\displaystyle \frac{AB^2}{2\cdot b}=\frac{16}{2b}.\)
Аналогично, рассмотрев треугольник \(SBC\), получим, что \(BQ = \displaystyle \frac{BC^2}{2\cdot b} = \frac{32}{2b}.\)
Тогда \(BQ=2PB\), точка \(P\) - середина \(BQ.\)
б) Найдем угол между \(SBA\) и \(SBC\), если \(SD=b=8.\)
\(AP\) и \(CQ\) – перпендикуляры к \(SB\), проведенные в плоскостях \(SAB\) и \(SBC\), точка \(P\) – середина \(BQ.\)
Пусть \(F\) – середина \(BC\), тогда \(PF\) – средняя линия \(\triangle BQC, \ PF \parallel QC, \ PF \perp SB. \)
Угол \(APF\) найдем из треугольника \(APF.\)
Из \(\triangle ABF: \, AF=\sqrt{AB^2+BF^2}=\sqrt{16+8}=2\sqrt{6}.\)
Если \(SD=b=8, \, PB=1,\) то \(AP= \sqrt{AP^2-PB^2}=\sqrt{15}, \ BQ=2.\)
Тогда \(QC=\sqrt{BC^2-BQ^2}=\sqrt{32-4}=2\sqrt{7}.\)
\(PF=\displaystyle \frac{1}{2} QC=\sqrt7.\)
В треугольнике \(APF\) по теореме косинусов \(AF^2=AP^2+PF^2-2AP\cdot PF\cdot cos\angle APF;\)
\(24=15+7-2\cdot\sqrt{15}\cdot\sqrt{7}\cdot cos\angle APF;\)
\(cos\angle APF=\displaystyle \frac{-1}{\sqrt{105}}.\)
Поскольку угол между плоскостями – это меньший из углов, ими образуемых, угол \(\varphi\) между плоскостями \(ASB\) и \(BSC\) – это угол, смежный с углом \(APF.\)
\(cos \varphi =\displaystyle \frac{1}{\sqrt{105}};\)
\( \varphi =arccos\displaystyle \frac{1}{\sqrt{105}}.\)
5. Решите неравенство: \(log_{x^2}\left ( 3-x \right )\leq log_{x+2}\left ( 3-x \right ).\)
Решение:
ОДЗ: \(\left\{\begin{matrix} 3-x> 0, \\ x^2\ne0 , \\x^2\ne1 , \\x+2>0, \\ x+2\ne1; \end{matrix}\right. \: \: \left\{\begin{matrix} -2< x<3, \\ x\ne0,\: x\ne1,\\ x\ne-1 .\end{matrix}\right.\)
1) Рассмотрим случай \(3-x=1\), тогда \(x=2.\)
Получим: \(log_4 1 = log_4 1\), тождество.
2) Пусть \(3-x \ne1\). Применим формулу \(log_a b = \displaystyle \frac{1}{log_b a}.\)
\(\displaystyle \frac{1}{log_{3-x}x^2} - \frac{1}{log_{3-x}(x+2)} \leq 0;\)
\(\displaystyle \frac{log_{3-x}(x+2)-log_{3-x}x^2}{log_{3-x}x^2 \cdot log_{3-x}(x+2)} \leq 0.\)
Применяя метод рационализации и учитывая ОДЗ и условие \(3-x \ne 1\), получим:
\(\left\{\begin{matrix} -2 < x < 3,\\x\ne1,\: x\ne2 , \\ x\ne0,\: x\ne-1,\\ \displaystyle \frac{(2-x)(x+2-x^2)}{(2-x)(2-x)(x^2-1)(x+1)}\leq0 ; \end{matrix}\right.\)
\(\left\{\begin{matrix} -2 < x < 3 ,\\ x\ne1, \, \, x\ne2, \, x\ne0, \, x\ne-1 , \\ \displaystyle \frac{(x-2)^2}{(x+1)(x-1)}\leq0 .\end{matrix}\right.\)
Решая систему и объединяя с ответом в случае (1), получим:
\(x\in (-1;0)\cup (0;1)\cup { 2 }.\)
6. а) Решите уравнение \(\sqrt{2}\, cos\left ( 8x \right )cos\left ( x+\displaystyle \frac{\pi}{4} \right )=2cos\displaystyle \frac{\pi}{4}.\)
б) Укажите корни этого уравнения, принадлежащие отрезку \([-3\pi; 5\pi].\)
Решение:
а) Так как \(cos \displaystyle \frac{\pi}{4} = \frac{\sqrt{2}}{2},\) получим:
\(\sqrt{2} cos \, 8x \cdot cos \left (x+ \displaystyle \frac{\pi}{4}\right )=\sqrt{2};\)
\(cos \,8x \cdot cos \left (\displaystyle \frac{\pi}{4}\right )=1.\)
Каждый из множителей в левой части уравнения по модулю не больше 1:
\(|cos 8x| \leq 1;\)
\(\left |cos \left (x+ \displaystyle \frac{\pi}{4}\right )\right | \leq 1.\)
Их произведение равно 1, только если
\(\left[ \begin{array}{ccc} \left\{\begin{matrix}cos\, 8x=1 ,\\cos \left (x+ \displaystyle \frac{\pi}{4}\right )=1, \end{matrix}\right. \\ \left\{\begin{matrix}cos\, 8x=-1 ,\\ cos \left (x+ \displaystyle \frac{\pi}{4}\right )=-1 ; \end{matrix}\right. \end{array} \right.\)
\(\left[ \begin{array}{ccc} \left\{\begin{matrix}8x=2\pi n, \, n\in Z , \\x+ \displaystyle \frac{\pi}{4} =2\pi k, \, k\in Z, \end{matrix}\right. \\\left\{\begin{matrix}8x= \pi+2\pi n , \\ x=\displaystyle \frac{\pi}{4}=\pi+2\pi k; \end{matrix}\right. \end{array} \right.\)
\(\left[ \begin{array}{ccc} \left\{\begin{matrix}x=\displaystyle \frac{\pi n}{4},\, n\in Z ,\\x= - \displaystyle \frac{\pi}{4}+2\pi k, \, k \in Z, \end{matrix}\right. \; (1) \\\left\{\begin{matrix}x=\displaystyle \frac{\pi}{8}+\displaystyle \frac{\pi n}{4}, \\ x=\ - \displaystyle \frac{\pi}{4}+\pi +2 \pi k. \end{matrix}\right. \; (2) \end{array} \right.\)
Система (1):
\(\displaystyle \frac{\pi n}{4}= - \frac{\pi}{4}+2\pi k \, n, \ k \in Z;\)
\(n = -1+8k,\) тогда \(x= - \displaystyle \frac{\pi}{4}+2\pi k , \, k \in Z.\)
Система (2):
\(\displaystyle \frac{\pi}{8}+\frac{\pi n}{4}=-\frac{\pi}{4}+\pi+2\pi k ,\, n, \ k \in Z.\)
\(\displaystyle \frac{1}{4} + \frac{1}{8} + \frac{n}{4} = 1+2k;\)
\(\displaystyle \frac{1}{2} + n =3 +8k, \, n, \ k \in Z.\)
Уравнение не имеет целых решений, так как левая часть — не целое число, правая — целое.
Получим ответ в пункте (a):
\(x= -\displaystyle \frac{\pi}{4}+2 \pi k ,\, k \in Z.\)
б) Отберём корни на отрезке \([-3\pi; 5\pi)\) с помощью двойного неравенства.
\(-3 \pi \leq \ -\displaystyle \frac{\pi}{4}+2 \pi k \leq 5\pi;\)
\(-12 \leq -1+8k \leq 20;\)
\(-11 \leq 8k \leq 21;\)
\(- \displaystyle \frac{11}{8} \leq k \leq \frac{21}{8};\)
\(k= -1; \ 0; \ 1; \ 2.\)
\(x= - \displaystyle \frac{9\pi}{4}; \ - \frac{\pi}{4}; \ \frac{7\pi}{4}; \ \frac{15 \pi}{4}.\)