Анна Малкова

1. ЕГЭ. На экзамене по геометрии школьнику достанется одна задача из сборника. Вероятность того, что эта задача по теме «Параллелограмм», равна 0,35. Вероятность того, что это окажется задача по теме «Окружность», равна 0,45. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
Решение:
В сборнике нет задач, относящихся к обеим темам. Значит, получить на экзамене задачу по теме «Окружность» или по теме «Параллелограмм» – несовместные события.
Вероятность того, что произойдет одно из них, равна сумме вероятностей, \(p=0,35+0,45=0,8\).
Ответ: 0,8.
2. ЕГЭ. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение:
Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы.
Пусть \(p\) – вероятность того, что чайник прослужил больше года.
\(p_1\) – вероятность того, что он сломается на второй год, \(p_2\) – вероятность того, что он прослужит больше двух лет. Очевидно, \(p=p_1+p_2\).
Тогда \(p_1=p-p_2=0,93-0,87=0,06\).
Ответ: 0,06
3. ЕГЭ. Вероятность того, что новый сканер прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение:
С вероятностью 0,94 сканер прослужит больше года. Это значит, что он может или прослужить больше года, но меньше двух лет, или прослужить больше двух лет. Сумма вероятностей этих событий дает 0,94.
\(0,87+p=0,94,\)
\(P=0,94−0,87=0,07.\)
Ответ: \(0,07\).
4. ЕГЭ. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в автобусе окажется меньше 24 пассажиров, равна 0,81. Вероятность того, что окажется меньше 14 пассажиров, равна 0,6. Найдите вероятность того, что число пассажиров будет от 14 до 23.
Решение:
Пусть количество пассажиров в автобусе равно \(n\). Возможны два случая:
\(n <\) 24 с вероятностью 0,81 или
\(n\geq24\) с вероятностью \(1–0,81=0,19\).
Если \(n < 44\), то и здесь возможны два случая:
\(n < 14\) с вероятностью 0,6 или
\(14 \leq n \leq 23\) с вероятностью \(p\).
\(p+0,6=0,81,\)
\(p= 0,81 – 0,6 = 0,21.\)
Ответ: \(0,21\).
5. ЕГЭ. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше, чем 810 г, равна 0,97. Вероятность того, что масса окажется больше, чем 790 г, равна 0,92. Найдите вероятность того, что масса буханки больше, чем 790 г, но меньше, чем 810 г.
Решение:
Пусть масса буханки равна \(m\).
\(m < 810\) г с вероятностью \(0,97\) или
\(m \geq 810\) г с вероятностью \(1 – 0,97 = 0,03\).
Вероятность того, что \(m > 790\) г, равна \(0,92\).
Значит, с вероятностью \(1 – 0,92 =0,08\) масса буханки \(m \leq 790\) г.
Получаем 3 случая.
\(m \leq 790\) с вероятностью \(0,08\).
\(m \geq 810\) г с вероятностью \(0,03\).
Значит, \(790 < m < 810\) г с вероятностью \(1 – 0,08 – 0,03 = 0,89\).
Ответ: \(0,89\).
6. Вероятность того, что студент увлекается математикой и социологией одновременно, равна 0,092. Вероятность того, что студент увлечен социологией, равна 0,73. Найдите вероятность того, что студент увлечен математикой, если известно, что он увлекается социологией. Ответ округлите до тысячных.
Решение:
Это задача не из ЕГЭ, однако очень интересная.
Возьмем 1000 студентов. Из них 73 процента увлекаются социологией, это 730 студентов (а 270 студентов равнодушны к социологии). Где искать тех студентов, которые увлекаются и математикой, и социологией? - Конечно, среди этих 730, больше негде. Одновременно увлекаются математикой и социологией \(0,092\cdot1000=92\) студента. Теперь множество всех исходов - это 730 студентов (социология), множество благоприятных исходов - 92 студента (математика и социология), \(p=\displaystyle \frac{92}{730}\approx0,126\).
Ответ: \(0,126\).
Вот похожая задача:
7. В местном баре 72% посетителей играют в бильярд и пьют пиво. В бильярд играют 80% посетителей. В баре случайным образом выбирают посетителя. Найдите вероятность того, что он пьет пиво, если известно, что он играет в бильярд.
Напоминаем, что неумеренное потребление пива вредит здоровью.

8. С какой вероятностью при трех бросках монетки выпадет 3 орла?
Решение:
Вы бросаете монетку. Зависит ли выпадение орла или решки от того, что выпало на предыдущем броске? – Конечно, нет! Ведь монетка «не помнит», каким был результат предыдущего броска.
При каждом броске монеты вероятность выпадения орла равна \(\displaystyle \frac{1}{2}\).
При двух бросках вероятность выпадения двух орлов равна \(\displaystyle \frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}\)
А вероятность выпадения трех орлов при трех бросках монеты равна \(\displaystyle \frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{8}=0,125\).
Ответ: \(0,125\).
9. ЕГЭ. Стрелок попадает в цель с вероятностью 0,9. Найдите вероятность того, что он попадёт в цель четыре раза подряд.
Решение:
Будем считать, что результат стрелка не зависит от того, попал он или промахнулся в прошлый раз.
Тогда вероятность двух попаданий подряд равна \(0,9\cdot0,9=0,81\). А вероятность четырех попаданий подряд равна \(0,9\cdot0,9\cdot0,9\cdot0,9=0,6561\).
Ответ: \(0,6561\).
10. ОГЭ. Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два случайно выбранных из одной партии фонарика не будут бракованными?
Решение:
Вероятность того, что один фонарик не бракованный, равна \(1-0,02=0,98\).
Фонарики могут быть хорошими или бракованными независимо друг от друга.
Вероятность того, что два фонарика не будут бракованными, равна \(0,98^2=0,9604\).
Ответ: \(0,9604\).
11. Анна Малкова. Два грузовика, работая совместно, с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй - два. Вероятность застрять с грузом снега при подъеме в горку равна 0,2 для первого грузовика и 0,25 - для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?
Решение:
Вероятность для первого грузовика благополучно одолеть горку \(1-0,2=0,8\). Для второго \(1-0,75=0,25\). Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью
\(0,8\cdot0,75\cdot0,8\cdot0,75\cdot0,8=0,36\cdot0,8=0,288\).
Ответ: \(0,288\).
12. ЕГЭ. В магазине три продавца. Каждый из них занят обслуживанием клиента с вероятностью 0,7 независимо от других продавцов. Найдите вероятность того, что в случайный момент времени все три продавца заняты.
Решение:
Три продавца могут быть заняты независимо друг от друга. Вероятность того, что и первый занят, и второй, и третий занят – это произведение вероятностей трех событий.
\(p=0,7\cdot0,7\cdot0,7=0,343\).
Ответ: \(0,343\).
13. Найдите вероятность того, что в случайно выбранном телефонном номере последняя цифра чётная, а предпоследняя – нечётная?
Решение:
Всего у нас 10 цифр. Это 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Из них 5 четные (делятся на 2): 0, 2, 4, 6, 8.
И 5 нечетные (не делятся на 2): 1, 3, 5, 7, 9.
Случайно выбранная цифра четная с вероятностью \(\displaystyle \frac{1}{2}\). В случайно выбранном телефонном номере последняя цифра четна тоже с вероятностью \(\displaystyle \frac{1}{2}\).
Предпоследняя нечетна, вероятность этого \(\displaystyle \frac{1}{2}\).
А вероятность того, что последняя цифра четна и предпоследняя нечетна, равна \(\displaystyle \frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}=0,25\).
Ответ: \(0,25\).
14. Анна Малкова. Играя в снежки, Маша попадает в цель с вероятностью 0,8, а Наташа – с вероятностью 0,25. Маша и Наташа одновременно бросили снежки в Василия. С какой вероятностью в Василия попадет хотя бы один снежок?
Решение:
Найдем вероятность того, что в Василия не попадет ни один снежок, то есть и Маша промахнулась (вероятность этого события \(1–0,8=0,2\)), и Наташа независимо от нее промахнулась (вероятность этого события \(1–0,25=0,75\)). Получим:
\(0,2\cdot0,75=0,15\).
Вероятность противоположного события (в Василия попал хотя бы один снежок) равна \(1–0,15=0,85\).
Ответ: \(0,85\)
15. ЕГЭ. Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Нам подходят варианты, когда первая лампа перегорела, а вторая работает.
Или вторая перегорела, а первая работает.
Или обе работают.
Не подходит только вариант, когда обе перегорели.
Вероятность этого события равна \(0,2\cdot0,2=0,04\).
Противоположное событие – хотя бы одна лампа работает (это нам и нужно). Его вероятность равна \(1-0,04=0,96\).
Ответ: \(0,96\).
16. ЕГЭ. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук выйдет через выход А.
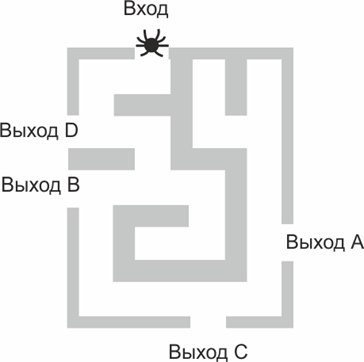
Решение:
Пронумеруем развилки, на которых паук может случайным образом свернуть в ту или другую сторону.
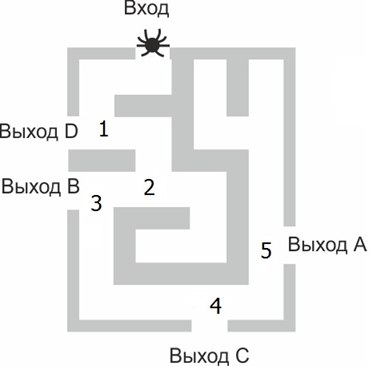
Он может либо выйти в выход D, и вероятность этого события равна \(\displaystyle \frac{1}{2}\). Либо уйти дальше в лабиринт. На второй развилке он может либо свернуть в тупик, либо выйти в выход В (с вероятностью \(\displaystyle \frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}\). На каждой развилке вероятность свернуть в ту или другую сторону равна \(\displaystyle \frac{1}{2}\), а поскольку развилок пять, вероятность выбраться через выход А равна \(\displaystyle \frac{1}{32}\), то есть \(0,03125\).
Ответ: \(0,03125\).
17. ЕГЭ. Если гроссмейстер А играет белыми, то он выигрывает у гроссмейстера Б с вероятностью 0,5. Если А играет черными, то А выигрывает у Б с вероятностью 0,3. Гроссмейстеры А и Б играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А выиграет оба раза.
Решение:
Согласно условию задачи, гроссмейстер А должен выиграть белыми и выиграть черными. Порядок не важен. Вероятность выигрыша в обеих партиях равна \(0,3\cdot0,5=0,15\).
Ответ: \(0,15\).
18. Говорят, что в старину каждый десятый на Руси был Иван, а каждый двадцатый Петр. Если это верно, то кого было больше: Иванов Петровичей или Петров Ивановичей?
Решение:
Можно по-разному решать эту задачу, и вероятностный подход здесь тоже применим. Посчитаем вероятности двух событий.
Событие А. Случайно выбранного мужчину зовут Иван Петрович.
Событие В. Мужчину зовут Петр Иванович.
Вероятность быть Иваном Петровичем для жившего в старину россиянина равна \(0,1\cdot0,05=0,005\). Мы перемножили вероятности того, что наш древнерусский житель – Иван и что его отца зовут Петр.
А вероятность оказаться Петром Ивановичем точно такая же: \(0,05\cdot0,1=0,005\).
Ответ: \(0,005\).
19. Анна Малкова. Математик М. не любит тонированные стекла в машинах, не переносит ароматизаторов воздуха и терпеть не может радио. Известно, что в 70% машин такси стекла тонированные, 75% таксистов вешают в машине ароматизатор воздуха, 80% водителей слушают радио, Математик М. вызывает такси. С какой вероятностью приехавшая машина будет удовлетворять всем требованиям математика М.?
Решение:
«Идеальное», с точки зрения М., такси – без тонированных стекол (с вероятностью 0,3), без ароматизатора (вероятность 0,25), без радио (вероятность 0,2). Произведение вероятностей равно \(0,3\cdot0,25\cdot0,2 = 0,015\) (полтора процента).
Ответ: \(0,015\)
20. Анна Малкова. Маша купила для всей семьи пирожков: 3 с капустой, 3 с вареньем и 4 с рисом. Пирожки лежат в одном пакете и внешне совершенно одинаковы. По дороге домой Маша чувствует непреодолимое желание съесть 2 пирожка, причем разных и не с рисом. С какой вероятностью ей удастся выбрать нужные пирожки из пакета?
Решение:
1) Благоприятными для Маши будут следующие варианты:
2) Первый пирожок, который она вытащит, будет с капустой, а второй с вареньем.
Наоборот – первый с вареньем, второй с капустой.
Вероятность достать пирожок с капустой из пакета, в котором всего 10 пирожков, равна \(\displaystyle \frac{3}{10}\). После того как этот пирожок вытащен, в пакете остается 9 пирожков, из которых 3 с вареньем. Значит, вероятность вытащить пирожок с вареньем равна \(\displaystyle \frac{3}{9}=\frac{1}{3}\), а вероятность достать пирожки с капустой и с вареньем равна \(\displaystyle \frac{3}{10}\cdot\frac{1}{3}=\frac{1}{10}\), поскольку эти события независимы.
Во втором варианте вероятность достать пирожок с вареньем равна \(\displaystyle \frac{3}{10}\), а вероятность вытащить после этого пирожок с капустой равна \(\displaystyle \frac{3}{9}\), произведение этих вероятностей также равно \(\displaystyle \frac{1}{10}\).
Сложив полученные вероятности, получаем: \(0,1 + 0,1 = 0,2\).
На первый взгляд кажется, что ответ должен быть в 2 раза меньше, то есть 0,1. Ведь Маша может достать пирожки из пакета одновременно. О каких же двух вариантах тогда идет речь?
Что же, представим себе, что Маша достает пирожки из пакета одновременно (и даже надкусывает их одновременно!) Но у нее в правой руке может быть пирожок с капустой, а в левой – с вареньем, или наоборот. Опять два варианта!
Можно рассуждать иначе: пусть Маша достает пирожки из пакета не одновременно, а с интервалом в 1 секунду, и получаются два варианта, которые мы рассмотрели. Сократим этот интервал до \(\displaystyle \frac{1}{2}\) секунды, до 0,01 секунды. Очевидно, ответ не должен зависеть от того, насколько быстро Маша доставала из пакета пирожки.
Ответ: \(0,2\).
Вот похожая задача из ЕГЭ:
21. ЕГЭ. В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Решение:
Всего в коробке 25 фломастеров.
В условии не сказано, какой из фломастеров вытащили первым – красный или синий.
Предположим, что первым вытащили красный фломастер. Вероятность этого \(\displaystyle \frac{9}{25}\), в коробке остается 24 фломастера, и вероятность вытащить вторым синий равна \(\displaystyle \frac{10}{24}\). Вероятность того, что первым вытащили красный, а вторым синий, равна \(\displaystyle \frac{9}{25}\cdot\frac{10}{24}=\frac{3}{5}\cdot\frac{1}{4}=\frac{3}{20}\).
А если первым вытащили синий фломастер? Вероятность этого события равна \(\displaystyle \frac{10}{25}=\frac{2}{5}\) Вероятность после этого вытащить красный равна \(\displaystyle \frac{9}{24}=\frac{3}{8}\), вероятность того, что синий и красный вытащили один за другим, равна \(\displaystyle \frac{2}{5}\cdot\frac{3}{8}=\displaystyle \frac{3}{20}\).
Значит, вероятность вытащить первым красный, вторым синий или первым синий, вторым красный равна \(\displaystyle \frac{3}{20}+\frac{3}{20}=0,3\).
А если их доставали из коробки не один за другим, а одновременно? Вероятность остается такой же: 0,3. Потому что она не зависит от того, вытащили мы фломастеры один за другим, или с интервалом в 2 секунды, или с интервалом в 0,5 секунды… или одновременно!
В этой задаче мы рассуждали так же, как и в предыдущей.
Ответ: \(0,3\).
22. ЕГЭ. Для подтверждения скидки магазин отправляет покупателю на телефон сообщение с трёхзначным кодом, ровно две из цифр которого совпадают. У Пети разряжен телефон. Какова вероятность того, что он случайно угадает код? Ответ округлите до тысячных.
Решение:
Узнаем сначала, сколькими способами можно составить код вида АВВ, в котором вторая и третья цифра совпадают.
Заметим, что первая цифра в трехзначном коде может быть равна нулю (а в трехзначном числе – не может).
Значит, первую цифру можно выбрать 10 способами. Это может быть 0, 1, 2… 9.
Для второй цифры остается 9 способов (любая цифра, кроме той, которая на первом месте).
Для третьей цифры только 1 способ, поскольку она такая же, как вторая.
Для комбинации АВВ получилось \(10 \cdot 9 = 90\) способов.
Для комбинации ВАВ (совпадают первая и третья цифры) – тоже 90 способов.
И для варианта ВВА (совпадают две первые) – тоже 90 способов, всего 270 способов составить код.
Пете подходит только один из 270 вариантов. Вероятность равна \(\displaystyle \frac{1}{270}\approx 0,004\).
Ответ: \(0,004\).
































