Анна Малкова
В вариантах ЕГЭ множество задач такого типа. Про куриные яйца из двух хозяйств. Про магазин, где продаются стекла для фар бракованные и небракованные. Про анализ на гепатит. Эти задачи мы решаем одним и тем же способом: строим «дерево» возможных исходов.
1. Анна Малкова. Мини-пекарня продает пирожки с мясом, однако в среднем 2 пирожка из 10 оказываются без мяса. Покупатель купил 2 пирожка. Найдите вероятность того, что хотя бы в одном из них найдется мясо.
Решение:
По условию, пекарня работает так, что каждый пирожок может случайным образом оказаться с мясом (с вероятностью \(\displaystyle \frac{4}{5}\)) или ни с чем (и вероятность этого события \(\displaystyle \frac{1}{5}\)).
Нарисуем схему возможных исходов:
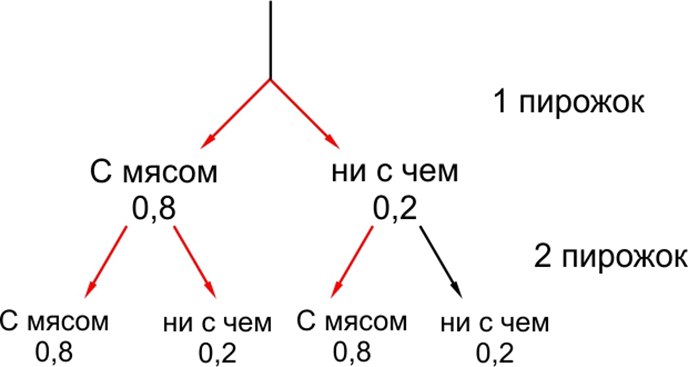
Благоприятные исходы в этой задаче – когда мясо будет только в первом пирожке, только во втором или в обоих. Не подходит только случай, когда оба пирожка окажутся без начинки. Вероятность этого исхода \(0,2\cdot0,2=0,04\). Тогда нужная нам вероятность равна \(1-0,04=0,96\).
В этой задаче пирожки могут оказаться без мяса независимо друг от друга.
Вероятность произведения независимых событий равна произведению их вероятностей. А вероятность суммы несовместных событий равна сумме вероятностей. Когда «и то, и другое» - вероятности перемножаются. Когда «или то, или другое» - вероятности складываются.
Ответ: 0,96
2. ЕГЭ. Склад оборудован двумя датчиками сигнализации различной конструкции, которые подают звуковой сигнал, если в помещение проникает посторонний. Вероятность выхода из строя в течение года для первого датчика равна 0,1 и второго 0,2. Найдите вероятность того, что в течение года хотя бы один датчик сигнализации останется исправным.
Решение:
Нарисуем схему возможных исходов.
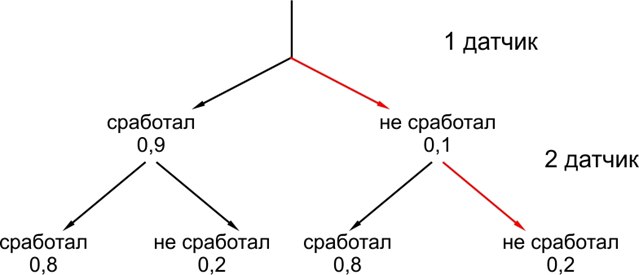
Нам подходят все исходы, кроме одного – когда в течение года сломались оба датчика. Вероятность этого, неблагоприятного для нас исхода, равна \(0,1 \cdot 0,2=0,02\).
Вероятность благоприятного исхода (хотя бы один датчик сработал) равна \(1-0,02=0,98\).
В этой задаче датчики также работают независимо друг от друга.
Ответ: 0,98
Следующая задача отличается от предыдущих. Однако и в ней мы рисуем «дерево» возможных исходов.
3. Анна Малкова. Маша – студентка МГУ. Если утром светит солнце, Маша посещает первую лекцию с вероятностью 0,7. Если в момент пробуждения Маши пасмурно, то с вероятностью 0,8 Маша снова засыпает и пропускает первую лекцию.
Утром 1 апреля вероятность солнечной погоды в Москве оценивается в 25%.
С какой вероятностью Маша будет присутствовать 1 апреля на первой лекции?
Решение:
Нарисуем «дерево» возможных исходов.
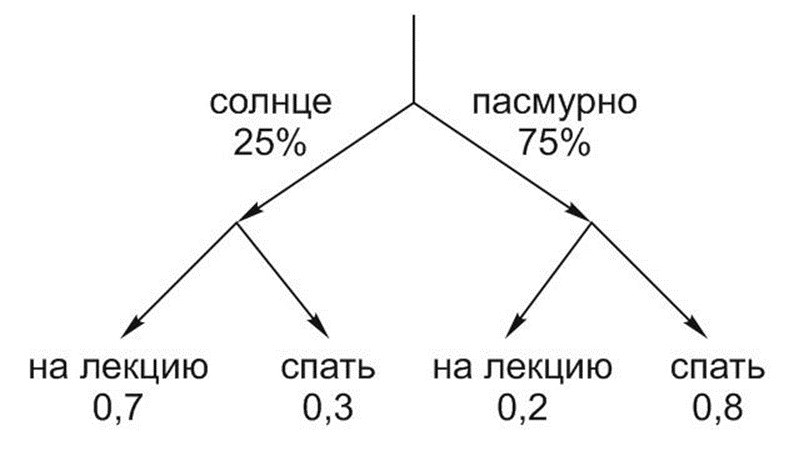
Вероятность присутствия Маши на первой лекции 1 апреля
\(p=0,25\cdot 0,7+0,75\cdot0,2=0,175+,015=,0325\)
В первых двух задачах, которые мы разобрали (про пирожки и датчики), речь шла о независимых событиях.
В задаче про Машу ситуация другая. Конечно, погода не зависит от того, пойдет Маша на лекцию или продолжит спать. Погода будет ясной или пасмурной независимо от поведения Маши.
А вероятность появления Маши на лекции зависит от погоды. Если светит солнце, Маша отправится на лекцию с вероятностью 0,7. Если пасмурно, то с вероятностью 0,3. Это условные вероятности, и о них вам наверняка рассказывали в школе. Прочитать о них можно в статье «Условная вероятность» на нашем сайте.
Но и в этом случаем мы строим дерево возможных исходов. А вероятность присутствия Маши на первой лекции мы посчитали по формуле полной вероятности.
Ответ: 0,325
В следующих задачах мы действуем аналогично.
4. ЕГЭ. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Изобразим все возможные исходы.
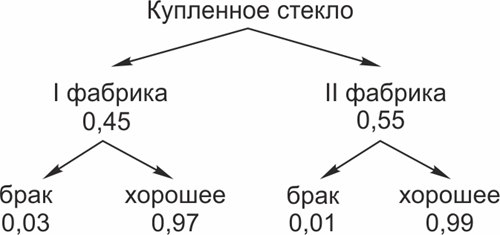
По условию, купленное в магазине стекло для автомобильной фары оказалось бракованным. Как это могло получиться?
Стекло сделано либо на первой фабрике, либо на второй. Эти события несовместны.
Вероятность того, что стекло с первой фабрики, равна 0,45.
Вероятность того, что стекло сделано на второй фабрике, равна 0,55.
Первая фабрика выпускает 3% бракованных стекол. Значит, с вероятностью 0,03 стекло, произведенное на первой фабрике, бракованное.
Вторая фабрика выпускает 1% бракованных стекол. Значит, с вероятностью 0,01 сделанное на ней стекло бракованное.
Покупатель купил бракованное стекло. Оно могло быть сделано на первой фабрике и оказалось бракованным. Вероятность произведения этих двух событий равна \(0,45\cdot0,03\).
Или другой случай. Стекло могло быть со второй фабрики и также бракованное. Вероятность одновременного наступления этих двух событий равна \(0,55\cdot0,01\). События «стекло с первой фабрики» и «стекло со второй фабрики» несовместны – они не могут случиться одновременно.
Вероятность суммы несовместных событий равна сумме вероятностей.
Значит, вероятность купить бракованное стекло равна:
\(0,45\cdot0,03 + 0,55\cdot0,01 = 0,019\).
Ответ: 0,019.
5. ЕГЭ. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Решение:
Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.
Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.
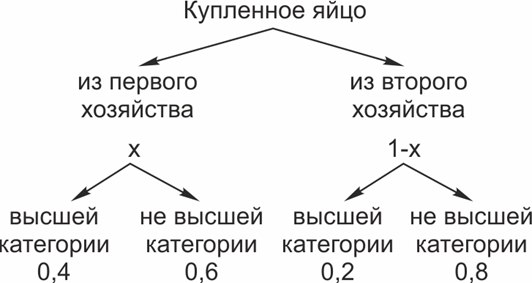
Пусть вероятность того, что купленное яйцо из первого хозяйства, равна \(x\). Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна \(1-x\).
Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% - не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.
Во втором хозяйстве 20% яиц высшей категории, а 80% - не высшей.
Пусть случайно выбранное в магазине яйцо - из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей: \(0,4x.\)
Вероятность того, что яйцо из второго хозяйства и высшей категории, равна \(0,2\cdot(1-x)\).
Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0,35.
Мы получили уравнение:
\(0,4x+0,2(1-x)=0,35\).
Решаем это уравнение и находим, что \(x=0,75\) – вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.
Ответ: 0,75
6. Анна Малкова. Магазин фермерских товаров закупает мёд в одинаковых банках у двух пчеловодов – Антона и Бориса, причем 65% мёда, который поставляет Антон, - это липовый мёд. У Бориса липовый мёд составляет 20% всего мёда, который он привозит в магазин. Известно, что 56% мёда, который продает магазин, - это липовый мёд. Найдите вероятность того, что случайно выбранная в магазине банка мёда произведена Борисом.
Решение:
Пусть \(x\) – вероятность того, что банка меда произведена на пасеке Бориса. Нарисуем «дерево» возможных исходов.
Банка меда может попасть в магазин с пасеки Антона с вероятностью \(1-x\). Поскольку 65% меда, который поставляетт Антон, - это липовый мед, вероятность того, что мед липовый и с пасеки Антона, равен \(0,65\cdot(1-x)\). Аналогично, вероятность того, что мед липовый и с пасеки Бориса, равна \(0,2x\).
Получим:
\(0,65(1-x)+0,2x=0,56;\)
\(45x=9;\)
\(x=0,2.\)
Ответ: 0,2.
7. Анна Малкова. Вероятность того, что клиент банка не вернет кредит, в период экономического роста равна 0,04, а в период экономического кризиса 0,2. Вероятность начала экономического кризиса оценивается в 0,45. Чему равна вероятность того, что клиент не вернет кредит?
Решение:
Как обычно, рисуем «дерево» возможных исходов. По условию задачи, экономический кризис начнется с вероятностью 0,45. С вероятностью 0,55 будет экономический рост.
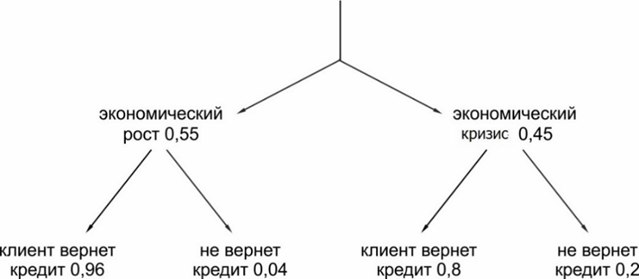
Вероятность того, что клиент не вернет кредит, равна \(0,55\cdot0,04+0,45\cdot0,2=0,112\).
Ответ: 0,112
8. Анна Малкова. По статистике, только 10% из тех, кто создает свой первый бизнес, достигают успеха. Из тех, кто вторично открывает свое дело, успеха достигают 90%. При этом только 8% из тех, у кого первый бизнес оказался неудачным, готовы стартовать еще раз. Найдите вероятность создания успешного бизнеса с первой или второй попытки.
Решение:
Нарисуем схему возможных исходов и отметим благоприятные.
Вероятность достичь успеха в бизнесе с первой попытки равна 0,1.
Вероятность достижения успеха со второй попытки равна 90% (как вы думаете, почему?)
Но эту вторую попытку еще надо рискнуть сделать, и на это способны только 8% из тех, у кого не получилось с первого раза.
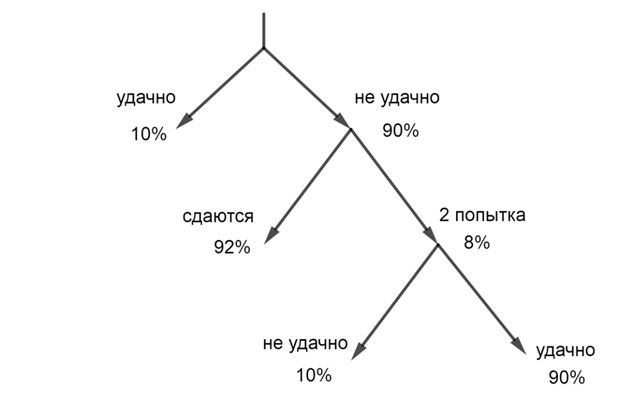
Получаем:
\(P=0,1+0,9\cdot0,08\cdot0,9=0,1648\) – вероятность создания успешного бизнеса с первой или второй попытки.
Ответ: 0,1648
9. Анна Малкова. Студентка Маша готовит на ужин макароны (с вероятностью 0,5), гречку (с вероятностью 0,3) или рис, причем выбор продукта происходит спонтанно. Макароны получаются съедобными с вероятностью 0,8, гречка – всегда, а рис с вероятностью 0,5. Студент Василий (женившийся на Маше) идет домой в предвкушении ужина. С какой вероятностью ужин окажется съедобным?
Решение:
Вероятность получить на ужин съедобные макароны равна \(0,5\cdot0,8=0,4\).
Гречка у Маши всегда готовится хорошо. Вероятность съесть гречку равна 0,3.
Наконец, рис, с которым всё непросто. Он получается у Маши пригодным в пищу с вероятностью \((1-0,5-0,3)\cdot0,5=0,2\cdot0,5=0,1\).
Поскольку события «на ужин макароны, гречка или рис» несовместны, получаем, что \(p=0,4+0,3+0,1=0,8\).
Ответ: 0,8.
10. Анна Малкова. Студент-биолог сдает тест, состоящий из четырех вопросов, причем вопросы для теста выбираются из списка случайным образом. Темы известны:
1-й вопрос – тема «Рыбы»,
2-й вопрос – тема «Рептилии»,
3-й вопрос – тема «Птицы»,
4-й вопрос – тема «Млекопитающие».
Каждый правильный ответ оценивается в 1 балл. Чтобы сдать тест, студенту достаточно набрать не менее 3 баллов. С какой вероятностью студент сдаст тест, если по теме «Рыбы» выучил 4 вопроса из 10 возможных, по теме «Рептилии» - 2 из 10, по теме «Птицы» - 5 из 10, зато по теме «Млекопитающие» знает ответ на любой из 10 возможных вопросов, которые могут встретиться в тесте?
Решение:
Каким бы ни был вопрос по теме «Млекопитающие», наш студент на него ответит и точно получит один балл. Осталось набрать еще не менее двух баллов.
Например, наш студент вначале занялся вопросом о рыбах. Вероятность ответить на вопрос о рыбах равна \(\displaystyle \frac{4}{10}\) (студент выучил по этой теме 4 вопроса из 10). Следующий вопрос о рептилиях, вероятность ответа \(\displaystyle \frac{2}{10}\). И еще вопрос о птицах – здесь вероятность получить балл равна \(\displaystyle \frac{5}{10}\).
Нарисуем «дерево» возможных исходов для вопросов про рыб, рептилий и птиц и отметим, в каких случаях студент получает за эти 3 вопроса не менее 2 баллов.
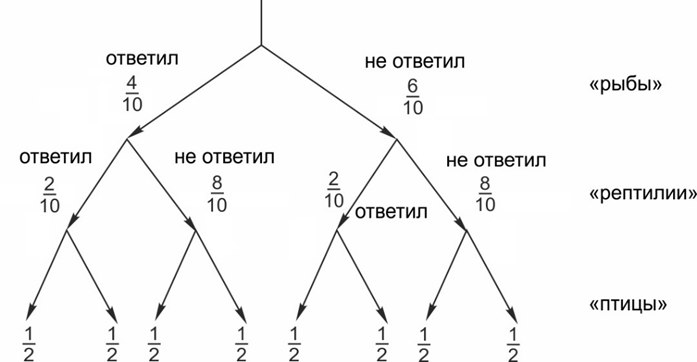
Считаем вероятность сдать тест:
\(P=\displaystyle \frac{4}{10}\cdot \frac{2}{10}\cdot \frac{1}{2}+\frac{4}{10}\cdot \frac{2}{10}\cdot \frac{1}{2}+\frac{4}{10}\cdot \frac{8}{10}\cdot \frac{1}{2}+\frac{6}{10}\cdot \frac{2}{10}\cdot \frac{1}{2}=0,3.\)
Ответ: 0,3
11. ЕГЭ. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Решение:
С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0,05 (то есть 5%). Вероятность того, что он здоров, равна 0,95 (то есть 95%).
Пациенту делают анализ. Покажем на схеме все возможные исходы:
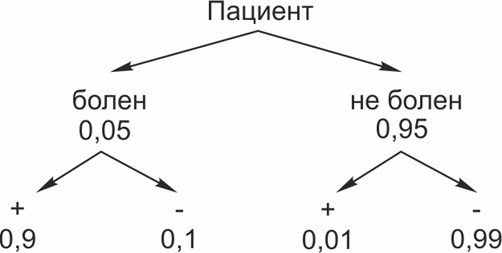
Если он болен гепатитом, анализ дает положительный результат с вероятностью 0,9. То есть анализ покажет: «есть гепатит».
Заметим, что анализ не во всех случаях выявляет гепатит у того, кто действительно им болен. С вероятностью 0,1 анализ не распознает гепатит у больного.
Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0,01. Тогда с вероятностью 0,99 анализ даст отрицательный результат, если человек здоров.
Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Благоприятные для этой ситуации исходы: человек болен, и анализ положительный (вероятность одновременного наступления этих двух событий равна \(0,05\cdot0,9\)), или человек здоров, и анализ ложный положительный (вероятность одновременного наступления этих двух событий равна \(0,95\cdot0,01\)). Так как события «человек болен» и «человек не болен» несовместны, то вероятность того, что результат анализа будет положительным, равна \(0,05\cdot0,9+0,95\cdot0,01=0,0545\).
Ответ: 0,0545.
12. Экзамен проходит по следующей схеме: если некоторый билет уже был вытянут, то после ответа экзаменатор откладывает его в сторону. Студент выучил 20 билетов из 30. Когда ему выгоднее идти, первым или вторым, чтобы вероятность вынуть выученный билет была больше?
Назовем билеты, которые студент выучил, «счастливыми».
Если студент пошел отвечать первым, вероятность вытянуть «счастливый» билет равна \(\displaystyle \frac{20}{30}=\frac{2}{3}\).
Если идти отвечать вторым, возможны два случая:
1) Первый билет, который вытянул кто-то другой, был «счастливым», и тогда «счастливых» билетов теперь 19.
2) Первый билет не был «счастливым», и «счастливых» билетов так и осталось 20.
Нарисуем схему возможных исходов, как делали раньше в подобных задачах:
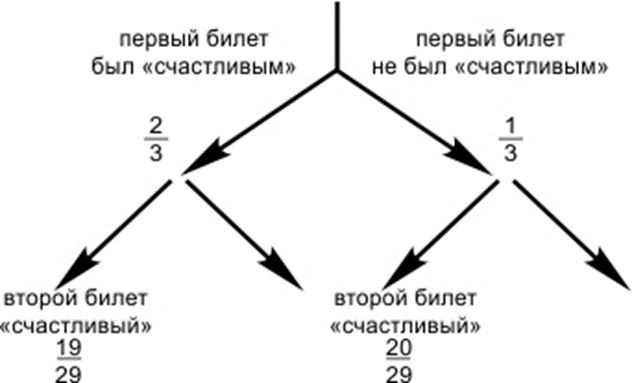
Вот наш студент идет отвечать вторым. Вероятность вытянуть «счастливый» билет равна \(\displaystyle \frac{2}{3}\cdot \frac{19}{29}+\frac{1}{3}\cdot \frac{20}{29}=\frac{2}{3}\).
Удивительный ответ! Та же самая вероятность! Значит, неважно, первым или вторым идти отвечать, если ты выучил 20 билетов из 30.
Ответ: не важно. Вероятность \(\approx0,66667\).
































