Анна Малкова
К задачам на вероятности сложных событий можно отнести и такие, где некоторое действие делается до результата.
Или получилось сразу. Или первый раз не получилось, а второй не получилось. Или не получилось первый раз, не получилось второй, а на третий раз – успех. Вот подборка таких задач.
1. Телефон передает sms-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше 2 попыток.
Решение:
По условию, либо сообщение удалось передать с первой попытки, либо со второй.
Вероятность того, что сообщение удалось передать с первой попытки, равна 0,4.
С вероятностью 0,6 с первой попытки передать не получилось. Если при этом получилось со второй, то вероятность этого события равна \(0,6\cdot 0,4\).
Значит, вероятность того, что для передачи сообщения потребовалось не более 2 попыток, равна \(0,4+0,4\cdot 0,6=0,4\cdot(1+0,6)=0,64\).
Можно посчитать и по-другому. Нам подходят случаи, когда удалось передать сообщение или с первой попытки, или со второй.
И не подходит только случай, когда не удалось передать сообщение ни с первой, ни со второй попытки. Не удалось с первой попытки с вероятностью 0,6. Со второй тоже с вероятностью 0,6. Значит, не удалось передать ни с первой, ни со второй попытки с вероятностью \(0,6\cdot 0,6=0,36\).
Нам нужна вероятность противоположного события (удалось передать или с первой, или со второй попытки). Эта вероятность равна \(1-0,36=0,64\).
Ответ: 0,64
В следующей задаче мы тоже посчитаем вероятность противоположного события.
2. Анна Малкова. Жил старик со своею старухой у самого синего моря. Старик ловил неводом рыбу, закидывая невод до тех пор, пока не поймает хотя бы одну. В результате многолетних наблюдений старик заметил, что вероятность поймать рыбу при первом закидывании невода равна 0,4, а при последующих 0,6. Сколько раз старику надо закинуть невод, чтобы вероятность поймать хотя бы одну рыбу была не менее 0,95?
Решение:
Закинув невод в первый раз, старик может поймать рыбу с вероятностью 0,4 или не поймать с вероятностью 0,6. Если старик поймал рыбу, он больше не ловит, если не поймал – продолжает закидывать.
Он может поймать рыбу с первой попытки, со второй, с третьей, с \(n\)-ной. Пусть вероятность события А = {старик поймал рыбу с одной из \(n\) попыток} не менее 0,95.
Тогда вероятность противоположного события В = {старик не поймал рыбу, сделав \(n\) попыток} не более 0,05. Это значит, что он не поймал рыбу с первой попытки, со второй, с третьей, с \(n\)-ной.
Вероятность этого события
\(p=0,6\cdot 0,4^{n-1}.\)
Получим:
\(0,6\cdot 0,4^{n-1}\leq 0,05;\)
\(0,4^{n-1}\leq \displaystyle \frac{0,5}{6};\)
\(0,4^{n-1}\leq \displaystyle \frac{1}{12};\)
\(\displaystyle \frac{1}{12} \approx 0,083;\)
\(0,4^2=0,16 > 0,083;\)
\(0,4^3=0,064 < 0,083.\)
Неравенство выполняется, если \(n-1=3\), тогда \(n=4\).
Ответ: 4
3. Арлен Близаров. Каждый вечер Хуан Гарсия играет на гитаре под окном неприступной красавицы Сесилии Кончиты. Вероятность того, что она в знак любви бросит ему красную розу, равна 0,1 в отдельно взятый вечер. Какие шансы, что Хуан Гарсия завоюет сердце Сесилии Кончиты, если её соседи согласны терпеть его бренчание только четыре вечера?
Решение:
Вероятность получить красную розу в отдельно взятый вечер равна 0,1. Хуан Гарсия, если повезет, получит ее в первый вечер. Тогда он приглашает Кончиту на свидание и больше под окном не бренчит. Хуан Гарсия может получить красную розу во второй, в третий или в четвертый вечер, причем вероятности каждого из этих событий разные.
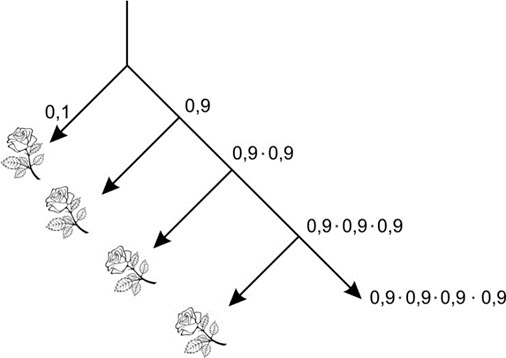
В первый вечер: вероятность получить красную розу равна \(0,1\).
Во второй вечер: \(0,9\cdot 0,1\) – поскольку с вероятностью \(0,9\) Хуан Гарсия во второй вечер вообще оказался под окном Сесилии Кончиты, а не на свидании с ней.
В третий вечер: \(0,9\cdot 0,9\cdot 0,1.\)
В четвертый вечер: \(0,9\cdot 0,9\cdot 0,9\cdot 0,1.\)
Получаем, что вероятность для Хуана Гарсии завоевать сердце Сесилии Кончиты равна
\(0,1+0,9\cdot 0,1+0,9\cdot 0,9\cdot 0,1+0,9\cdot 0,9\cdot 0,9\cdot 0,1=0,3439\).
Можно решить проще!
Вероятность того, что Хуан Гарсия так и не добился взаимности Сесилии Кончиты, равна
\(P_1=0,9\cdot 0,9\cdot 0,9\cdot 0,9=0,6561\).
Вычитая из единицы это число, получим вероятность благоприятного исхода для Хуана Гарсии: \(1-0,6561=0,3439\).
Ответ: 0,3439
4. Стрелок в тире стреляет по мишени. Известно, что он попадает в цель с вероятностью 0,3 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать этому стрелку, чтобы вероятность поражения цели была не менее 0,6?
Решение:
Пусть у стрелка есть \(n\) патронов. Стрелок может поразить цель первым, вторым… \(n\)-ным выстрелом, и все эти исходы для нас благоприятны. Не подходит только один исход – когда стрелок \(n\) раз стрелял и каждый раз был промах.
Вероятность промаха при одном выстреле равна \(1 - 0,3 = 0,7\).
Вероятность \(n\) промахов (из \(n\) выстрелов) равна \(0,7^n\), а вероятность попасть с первого или со второго … или с \(n\)-го выстрела равна \(1-0,7^n\).
По условию, \(1-0,7^n\geq 0,6,\)
\(0,7^n\leq 0,4.\)
Если \(n=2\), то \(0,7^2=0,49\) – не подходит, для \(n=3\) условие выполнено,
\(0,7^3=0,343 < 0,4\); хватит 3 патронов.
Ответ: 3.
































