Анна Малкова
Угол между двумя секущими (с вершиной вне окружности) равен полуразности дуг, высекаемых секущими на окружности.
Доказательство:
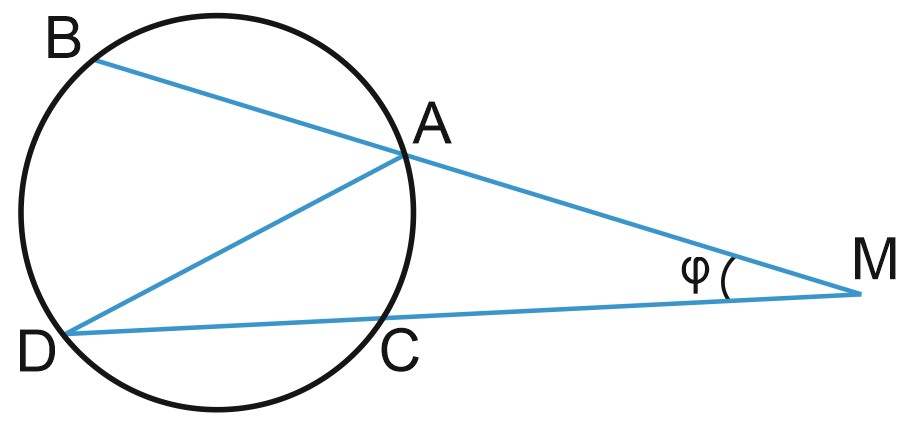
Пусть \(\varphi\) – угол между секущими \(MB\) и \(MD\). Докажем, что \(\varphi=\displaystyle\frac{\breve{BD}-\breve{AC}}{2}\).
Угол \(DAB\) – вписанный. Его величина равна половине угловой величины дуги \(BD\).
Угол \(ADC\) – вписанный. Его величина равна половине угловой величины дуги \(AC\).
Поскольку \(\angle DAB\) – внешний угол треугольника \(МAD, \; \angle DAB= \angle ADC+ \angle \varphi\). Отсюда \(\varphi=\displaystyle \frac{\breve{BD}-\breve{AC}}{2}\).