Анна Малкова
Условной вероятностью \(p(A|B)\) называют вероятность события \(A\) при условии, что событие \(B\) наступило.
\(p(A|B)=\frac{p(AB)}{p(B)}\)
И определение, и формула требуют объяснения. Чтобы понять, что такое условная вероятность, мы начнем с полезного лайфхака.
1. В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Решение:
Пусть население города составляет 10000 человек (мужчин и женщин).
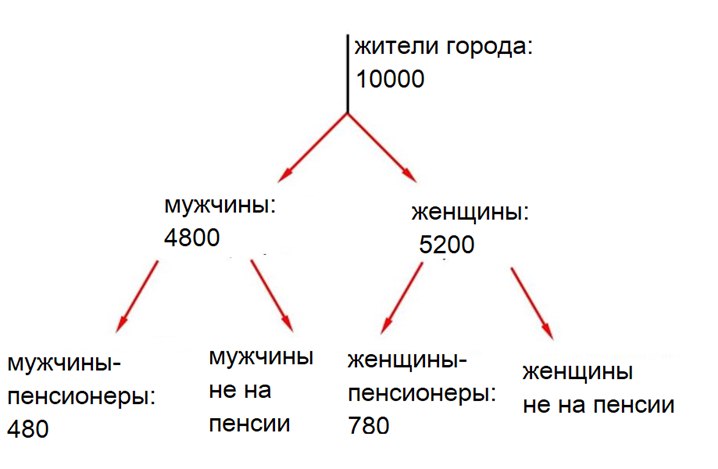
Количество взрослых мужчин в городе: 48 % от 10000, то есть 4800 человек.
Тогда количество женщин в городе равно 5200.
Из них \(0,15\cdot 5200=780\) женщин-пенсионеров (15 процентов от общего числа женщин).
Всего пенсионеров \(0,126\cdot 10000=1260\).
Тогда количество мужчин-пенсионеров равно \(1260 - 780 = 480\).
Вероятность для случайно выбранного мужчины оказаться пенсионером равна отношению числа мужчин-пенсионеров к числу мужчин в городе, то есть \(480:4800=0,1\).
Ответ. 0,1.
Следующую задачу решим подробно, двумя способами.
2. Анна Малкова
По данным социологического опроса, только 10% учащихся 11-х классов читали «Войну и мир» Л. Н. Толстого, а остальные не читали. Узнав об этом, министр просвещения приказал провести зачет по роману «Война и мир» во всех школах страны. В результате среди тех, кто не читал «Войну и мир», зачет сдали 20%, а среди тех, кто читал - 70%. С какой вероятностью случайно выбранный старшеклассник, который сдал зачет, действительно читал «Войну и мир»?*
*Ситуация вымышленная, возможные совпадения случайны.
Решение:
Пусть тест зачет сдавали 10000 учащихся (он ведь проходил во всех школах страны!).
Из этих 10000 учащихся только 1000 человек читали «Войну и мир», а 9000 – не читали.
Из читавших «Войну и мир» зачет сдали 70%, то есть 700 учеников.
Из не читавших сдали 20%, то есть \(0,2\cdot 9000=1800\) учащихся.
Всего зачет сдали \(700 + 1800 = 2500\) школьников.
Из этих \(2500\) школьников только \(700\) читали «Войну и мир».
Вероятность того, что случайно выбранный школьник, сдавший зачет, читал «Войну и мир», равна \(700 : 2500 = 0,28\).
Обратите внимание – при таком подходе слово «вероятность» возникает только в самом конце решения.
Есть и другой способ решения.
Вероятность того, что случайно выбранный старшеклассник сдал зачет, равна \(0,1\cdot0,7+0,9\cdot0,2=0,25\).
Вероятность того, что случайно выбранный старшеклассник читал «Войну и Мир» и сдал зачет, равна \(0,1\cdot0,7=0,07\).
С другой стороны, эта вероятность равна \(x\cdot0,25\), где \(x\) – вероятность того, что сдавший зачет старшеклассник читал «Войну и Мир». Отсюда \(x=0,07:0,25=0,28\).
Вот откуда получается формула для условной вероятности \(p(A|B)=\frac{p(AB)}{p(B)}\). Ее можно записать в виде: \(p(AB)=p(A|B)\cdot p(B)\). Знакомая формула, произведение вероятностей.
Можно также сказать, что \(p(AB)=p(A|B)\cdot p(B)=p(B|A)\cdot p(A)\).
В нашей задаче вероятность \(p(A|B)\) - это вероятность того, что старшеклассник читал «Войну и мир» при условии, что он сдал зачет.
Вероятность \(p(AB)\) – это произведение вероятностей событий «старшеклассник читал «Войну и мир» и «старшеклассник, который читал «Войну и мир», сдал зачет». Она равна \(0,1\cdot0,7=0,07\).
А \(p(B)\) – это вероятность того, что старшеклассник сдал зачет. При этом он мог читать «Войну и мир», а мог и не читать. Она равна \(0,1\cdot0,7+0,9\cdot0,2=0,25\).
И тогда, согласно формуле, \(p(A|B)=\frac{p(AB)}{p(B)}=\frac{0,07}{0,25}=0,28\).
Ответ: 0,28.
3. Анна Малкова
Среди студентов 1 курса некоторого вуза 25% отличников. Среди студентов 2 курса этого же вуза 10% отличников. На съемки телепередачи пригласили 550 студентов первого и второго курса этого вуза, из которых 300 – первокурсники. Студент, случайным образом выбранный для интервью во время телепередачи, оказался отличником. С какой вероятностью это второкурсник?
Решение:
По условию, приглашены на съемки 300 первокурсников и 250 второкурсников.
Среди первокурсников 25% отличников, это 75 студентов.
Среди второкурсников 10% отличников, это 25 студентов.
Всего отличников \(75 + 25 = 100\), и 25 из них – второкурсники.
Считаем вероятность по определению,
\(р = 25 : 100 = 0,25\).
Ответ: 0,25
4. Известно, что 5% всех мужчин и 0,25 % всех женщин дальтоники (не различают цвета, например, красный и зеленый). Случано выбранное лицо страдает дальтонизмом. Какова вероятность, что он мужчина? Считать равным количество мужчин и женщин. Ответ округлите до тысячных.
Решение:
Пусть общее количество мужчин и женщин равно 20000.
Из них 10000 мужчин и 10000 женщин.
Из 10000 мужчин 5% дальтоники, их 500 человек.
Из 10000 женщин 0,25% дальтоники, их 25.
Всего дальтоников 525, из них 500 мужчины. Делим число мужчин дальтоников на общее число всех дальтоников, \(p =\frac{500}{525}=\frac{100}{105}=\frac{20}{21} \approx 0,952\).
Ответ: 0,952
5. Анна Малкова
Среди учащихся 11-х классов школы 100 человек сдают ЕГЭ по математике Профильного уровня. 55 из 100 готовятся к нему на курсах или с репетитором, 35 – самостоятельно, остальные не готовятся, но верят, что все будет хорошо.
По статистике, собранной за несколько лет учителем математики этой школы, вероятность написать Пробный ЕГЭ в ноябре не ниже 70 баллов равна 0,8 для тех, кто занимается на курсах или с репетитором. Для тех, кто готовится самостоятельно, вероятность написать Пробный не ниже 70 баллов равна 0,6. Для тех, кто не готовится, вероятность получить на Пробном не ниже 70 баллов равна 0,2.
В ноябре 2022 года все 100 учащихся написали Пробный ЕГЭ. Учитель математики берет на проверку случайно выбранную работу учащегося. С какой вероятностью эта работа будет оценена не ниже, чем в 70 баллов?
Решение:
Получить не менее 70 баллов может ученик, который готовился на курсах или с репетитором (с вероятностью 0,8) или самостоятельно (с вероятностью 0,6) или не готовился совсем (с вероятностью 0,2).
\(p=0,55\cdot0,8+0,35\cdot0,6+0,02=0,44+0,21+0,02=0,67\)
Ответ: 0,67
6. Анна Малкова
Предположим, что в условиях предыдущей задачи учитель математики проверил случайно выбранную работу и поставил за нее 72 балла. С какой вероятностью эта работа написана учеником, который никак не готовился к ЕГЭ по математике?
Результат округлите до сотых.
Решение: в предыдущей задаче мы нашли, что с вероятностью 0,67 работа оценена не ниже 70 баллов. Значит, 67 из 100 учеников получили не ниже 70 баллов. Из 100 человек 10 никак не готовятся и с вероятностью 0,2 получают не ниже 70 баллов. Значит, 2 человека ника не готовились и получили не ниже 70.
Вероятность равна \(\frac{2}{67}\approx 0,03\).
Ответ: 0,03
7. За наблюдаемый период на 90% всех дней приходилась ясная погода. Гидрометцентр в тот же период предсказывал верную погоду в 74 случаях из 100, причем в 80% всех случаев, когда на день приходилась ясная погода, предсказания Гидрометцентра сбывались. С какой вероятностью погода оказалась пасмурной в тот день, когда Гидрометцентр предсказал пасмурную погоду?
Решение:
Это задача на условную вероятность. Можно задать вопрос так: «С какой вероятностью погода оказалась пасмурной в определенный день при условии, что Гидрометцентр предсказал в этот день пасмурную погоду».
Возьмем период 100 дней.
Из них 90 ясные, 10 пасмурные.
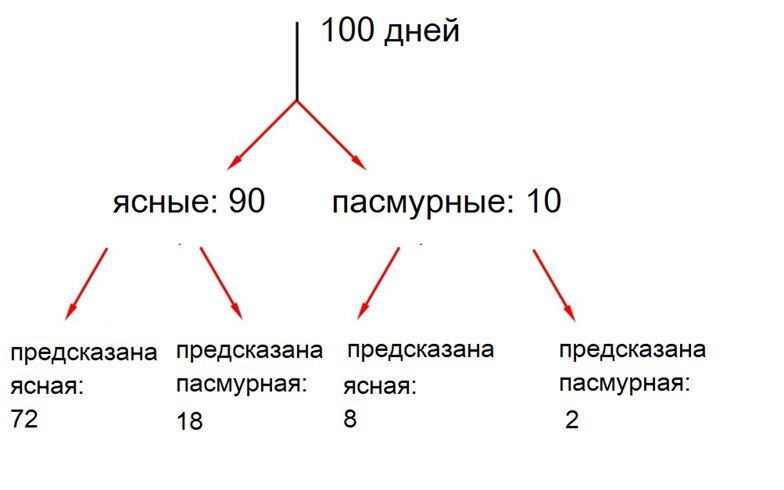
Была ясная погода и предсказана ясная: \(0,8\cdot90=72\) дня.
Поэтому \(90 - 72 = 18\) дней была ясная погода, а предсказана пасмурная.
По условию, погода была предсказана правильно в 74% случаев ( 74 дней из 100).
Значит, погода была пасмурная и предсказана пасмурная: \(74 - 72 = 2\) дня.
Всего дней, когда предсказана пасмурная погода, \(18+ 2 = 20\).
Из них 2 дней действительно была пасмурная погода, \(p=2:20=0,1\).
Ответ: 0,1
Можно было решать эту задачу и с помощью формулы условной вероятности. Но мы обошлись без нее.
Следующую задачу я придумала во время пандемии. Пункты (а) и (б) подготовительные, в пункте (в) – условная вероятность.
8. Анна Малкова
Однажды, в одной далекой галактике, гуманоидная раса столкнулась с атакой неизвестного вируса. Возможно, что в результате цепочки случайностей вирус вырвался из лаборатории. А может быть, его занес на планету корабль космических контрабандистов. Ученым гуманоидам удалось изобрести вакцину, эффективность действия которой была близка к 100%, но не равна 100%. Психология гуманоидов такова, что 95% из них готовы сразу воспользоваться вакциной, а 5% не сделают этого никогда. Через 2 месяца выяснилось, что вероятность заболеть для вакцинированного гуманоида равна 1%, а для невакцинированного 50%.
а) Сравнив число заболевших среди вакцинированных и невакцинированных, гуманоиды сказали, что вакцина бесполезна. Верно ли это утверждение?
б) Гуманоид Z. возвращается на родную планету из многолетней космической экспедиции. С какой вероятностью Z. подцепит заболевание, вызванное этим вирусом?
б) Через месяц после возвращения Z все-таки заболел. С какой вероятностью Z. был вакцинирован? Результат округлите до сотых.
Решение:
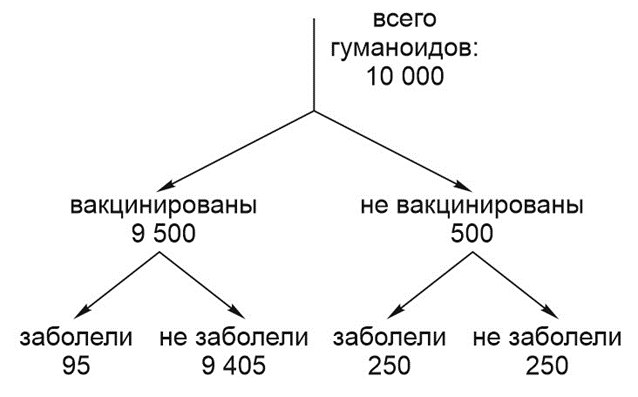
а) Чтобы ответить на вопрос пункта (а), надо повторить то, что сделали гуманоиды: сравнить число заболевших вакцинированных и невакцинированных.
Возьмем группу в 10000 гуманоидов. Из них 95% сразу сделали прививку (это 9500 гуманоидов). Оставшиеся 500 не станут пользоваться вакциной никогда.
Из вакцинированных заболел 1%, и это 95 гуманоидов. Из невакцинированных – 50%, что составляет 250 гуманоидов. Теперь понятно, почему жители планеты решили, что вакцина бесполезна: количество заболевших вакцинированных (это 95) и заболевших невакцинированных (а это 250) сравнимы друг с другом. Оценивать здесь нужно вероятность заболеть в том и в другом случае
б) Гуманоид Z может заболеть в двух случаях: если он сделал прививку и все-таки заболел или если он не вакцинировался и заболел. Поскольку из 10000 гуманоидов заболели \(90 + 250 = 345\), вероятность заболеть для Z равна \(345 : 10000 = 0,0345\).
в) В этом пункте задачи речь идет об условной вероятности: с какой вероятностью Z был вакцинирован, если известно, что он все-таки заболел. Воспользуемся нашей схемой. Среди 10000 гуманоидов число заболевших (вакцинированных и невакцинированных) равно 345, из них 95 вакцинированных. Значит, вероятность того, что Z был вакцинирован при условии, что он приобрел заболевание, равна \(95 : 345 = 19 : 69 \approx 0,28\).
Ответ:
a) нет, неверно
б) 0,0345
в) 0,28
9. Анна Малкова
а) Студент Василий работает репетитором по математике. Он надеется, что хоть кто-нибудь из его учеников получит на ЕГЭ не меньше 90 баллов. Василий считает, что из его учеников на это способны четверо. Люба может получить не меньше 90 баллов с вероятностью 0,9. Антон может получить такой результат с вероятностью 0,7; Марина с вероятностью 0,5 и Костя с вероятностью 0,4. С какой вероятностью надежды Василия сбудутся?
б) Студент Василий видит во сне, что только один из его учеников получил результат не меньше 90 баллов (он не понимает, кто именно). Он помнит, что Люба может получить не меньше 90 баллов с вероятностью 0,9. Антон может получить такой результат с вероятностью 0,7; Марина с вероятностью 0,5 и Костя с вероятностью 0,4. С какой вероятностью это была Люба? Ответ округлите до сотых.
Решение:
Василию подходит любой вариант, кроме одного: когда ни один ученик не получил 90 и выше баллов.
\(p=1-0,3\cdot0,1\cdot0,5\cdot0,6=0,991\).
Ответ: 0,991
б) Найдем вероятности того, что только Люба получила не менее 90 баллов, или только Антон, или только Марина, или только Костя.
Найдем вероятность того, что только один четверых учеников получил не ниже 90 баллов:
| Вероятность получить не менее 90 баллов | Вероятность получить менее 90 баллов | Вероятность того, что только этот ученик получил не менее 90 баллов, а остальные – меньше 90 | |
| Люба | 0,9 | 0,1 | \(0,9\cdot0,3\cdot0,5\cdot0,6=p_1\) |
| Антон | 0,7 | 0,3 | \(0,7\cdot0,1\cdot0,5\cdot0,6=p_2\) |
| Марина | 0,5 | 0,5 | \(0,5\cdot0,1\cdot0,3\cdot0,6=p_3\) |
| Костя | 0,4 | 0,6 | \(0,4\cdot0,1\cdot0,3\cdot0,5=p_4\) |
\(p=p_1+p_2+p_3+p_4=0,5(0,9\cdot0,3\cdot0,6+0,7\cdot0,1\cdot0,6+0,1\cdot0,3\cdot0,6+0,4\cdot0,1\cdot0,3)=\)
\(=\frac{0,5}{1000}\cdot(9\cdot3\cdot6+7\cdot6+3\cdot6+4\cdot3)=\frac{0,5}{1000}\cdot(27\cdot6+10\cdot6+2\cdot6)=\)
\(=\frac{0,5\cdot6}{1000}\cdot(27+10+2)=\frac{0,5\cdot6}{1000}\cdot39\).
Вероятность того, что только Люба получила не меньше 90 баллов:
\(p_1=0,9\cdot0,3\cdot0,5\cdot0,6=\frac{0,5}{1000}\cdot9\cdot3\cdot6\).
Событие «Только Люба получила не менее 90 баллов» можно представить как произведение двух событий: «Только один из учеников получил не менее 90 баллов» и «Именно Люба получила не менее 90, при условии, что только один ученик получил не менее 90».
Вероятность события «Только Люба получила не менее 90 баллов» - это мы ее нашли.
Вероятность события «Именно Люба получила не менее 90, при условии, что только один ученик получил не менее 90» нам надо найти. Обозначим ее \(p^\ast\) .
Тогда
\(p_1=p\cdot p^\ast \)
\(p^\ast =\frac{p_1}{p}=\frac{\not{0,5}\cdot9\cdot3\cdot6\cdot\not{1000}}{\not{1000}\cdot\not{0,5}\cdot6\cdot39}=\frac{9\cdot3}{13\cdot3}=\frac{9}{13}\approx 0,69\).
Ответ: 0,69
10. Татьяна Сиротина
Барон Мюнхгаузен в 80% случаев рассказывает небылицу. Если его рассказ – выдумка, то в 60% случаев ему не верят. А, если его рассказ правдив, то ему верят в 95% случаев.
а) Какова вероятность, что слушатели не поверят новому рассказу Барона Мюнхгаузена?
б) Барон рассказал историю о том, как он первый раз влюбился. Слушатели не поверили. С какой вероятностью эта история была правдой? Ответ округлите до сотых.
Решение:
а) Ситуация, при которой слушатели не поверят Барону Мюнхгаузену, может сложиться в результате следующих событий: рассказ действительно небылица и слушатели не поверили рассказчику или рассказ – правда, но слушатели не поверили.
Вероятности этих событий равны соответственно \(0,8\cdot0,6=0,48\) и \(0,2\cdot0,05=0,01\).
События «слушатели поверили Барону Мюнхгаузену» и «слушатели ему не поверили» образуют полную группу (они несовместны, и одно из них непременно происходит), поэтому можно применить формулу полной вероятности.
Получим: \(p=0,48+0,01=0,49\).
б) Вероятность того, что слушатели не поверили Барону Мюнхгаузену, равна 0,49. Это мы нашли в пункте (а).
Обозначим за \(x\) вероятность того, что рассказ Мюнхгаузена о его первой влюбленности был правдив при условии, что слушатели ему не поверили.
Тогда \(0,49x\) – вероятность того, что слушатели не поверили, но при этом рассказ был правдой.
С другой стороны, эта вероятность равна \(0,2\cdot0,05\).
Получим: \(0,2\cdot0,05=0,49x\); \(x=\frac{1}{49}\approx 0,02\).
Ответ:
а) 0,49
б) 0,02
11. Доля спама* в российском e-mail трафике составляет 75%. Почтовая программа распознает и отсеивает 95% этих писем. Однако по ошибке отсеивается также 1% нужной корреспонденции. Все остальные письма попадают в папку «Входящие».
С какой вероятностью письмо, попавшее в папку «Входящие», не является спамом? Результат округлите до сотых.
* - Спам - массовая рассылка корреспонденции рекламного характера лицам, не выражавшим желания её получить.
Решение:
Письмо может оказаться в папке «Входящие» в двух случаях:
1) если это – не спам и почтовая программа это распознала
2) это спам, и почтовая программа его пропустила.
Вероятности этих событий равны соответственно \(0,25\cdot0,99\) и \(0,75\cdot0,05\).
Применим формулу полной вероятности. Получим:
\(P=0,25\cdot0,99+0,75\cdot0,05=0,25\cdot(0,99+3\cdot0,05)=0,285\) – вероятность того, что письмо попало во «Входящие».
Обозначим за \(x\) вероятность того, что письмо, оказавшееся в папке «Входящие», не является спамом.
Тогда вероятность того, что письмо попало в папку «Входящие» и не является спамом, равна \(0,285x\).
С другой стороны, эта вероятность равна \(0,25\cdot0,99\).
Получим: \(0,25\cdot0,99=0,25\cdot1,14x\); отсюда \(x=\frac{99}{114}=\frac{33}{38}\approx 0,87\).
В этой задаче можно действовать так же, как и предыдущих: сказать, что всего на электронную почту отправлено 10000 писем и считать количество спама и не спама, а также писем из той и другой категории, попавших в папку «Входящие».
Ответ: 0,87
12. Анна Малкова
Узнав о появлении компьютерного вируса Angry worm*, пользователь Фил защитил свой ноутбук новой антивирусной программой, которая приостанавливает работу компьютера при подозрении на вирус.
Известно, что в случае наличия вируса Angry worm на компьютере программа распознает его с вероятностью 0,9.
Если компьютер не заражен этим вирусом, программа может дать сигнал ложной тревоги с вероятностью 0,02.
Известно также, что в день, когда Фил запускает антивирус на своем ноутбуке, 4% всех компьютеров в мире заражены вирусом Angry worm.
а) С какой вероятностью работа ноутбука Фила будет приостановлена в день запуска антивирусной программы?
б) После того как Фил запустил антивирус, работа его ноутбука была приостановлена, и на экране появилось сообщение о заражении вирусом Angry worm. С какой вероятностью ноутбук Фила действительно заражен этим вирусом? Результат округлите до сотых.
*Название вымышленное, возможные совпадения случайны.
Решение:
а) Вероятность присутствия вируса Angry worm на ноутбуке Фила равна 0,04 (поскольку 4% всех компьютеров в мире заражены этим вирусом). Фил еще не знает, есть ли вирус на его ноутбуке. Новая антивирусная программа может распознать (или не распознать) вирус, если он есть. Она может также дать «сигнал ложной тревоги» и остановить работу ноутбука, если вируса нет.
Покажем на схеме все возможные исходы:
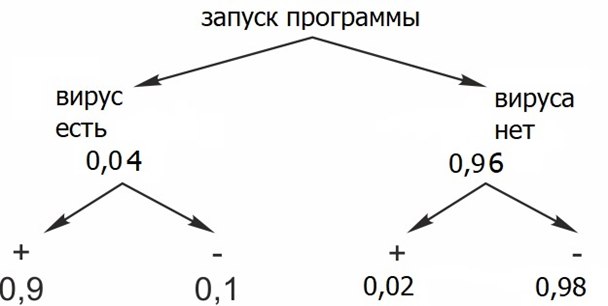
Найдем вероятность того, что программа приостановит работу ноутбука.
Благоприятные для этой ситуации исходы: на ноутбуке есть вирус, и программа его распознала (вероятность одновременного наступления этих двух событий равна \(0,04\cdot0,9\) или вируса нет, но программа дала «сигнал ложной тревоги» (вероятность одновременного наступления этих двух событий равна \(0,96\cdot0,02\)). Так как события «вирус есть» и «вируса нет» несовместны, то вероятность того, что антивирусная программа приостановит работу ноутбука, равна \(0,04\cdot0,9+0,96\cdot0,02=0,0552\).
б) В пункте (а) мы нашли, что антивирусная программа срабатывает с вероятностью 0,0552. При этом компьютер не обязательно заражен вирусом (может быть «ложная тревога»).
Пусть \(x\) - вероятность того, что ноутбук Фила действительно заражен вирусом при условии, что сработала антивирусная программа. Тогда \(0,0552x\) – вероятность произведения этих событий. С другой стороны, эта вероятность равна \(0,04\cdot0,9\) (вирус есть, и программа его распознала).
Получим: \(0,0552x=0,04\cdot0,9\)
\(x=\frac{0,04\cdot 0,9}{0,552}=\frac{360}{552}=\frac{15}{23}\approx 0,65\).
Ответ:
а) 0,0552
б) 0,65
В этой задаче (как и в предыдущей) речь идет об условной вероятности.
В нашем случае событие А – это срабатывание антивирусной программы, событие В – что при этом условии компьютер действительно заражен вирусом.
13. При подозрение на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.
Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Решение:
Задача похожа на уже знакомую тем, кто готовится к ЕГЭ (про гепатит), однако вопрос здесь другой.
Уточним условие: "Какова вероятность того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание?". В такой формулировке множество возможных исходов - это число пациентов с положительным результатом ПЦР-теста, причем только часть из них действительно заболевшие.
Пациент приходит к врачу и делает ПЦР-тест. Он может быть болен этим заболеванием – с вероятностью \(x\). Тогда с вероятностью \(1-x\) он этим заболеванием не болен.
Анализ пациента может быть положительным по двум причинам:
а) пациент болеет заболеванием, которое нельзя называть, его анализ верен; событие А,
б) пациент не болен этим заболеванием, его анализ ложно-положительный, событие В.
Это несовместные события, и вероятность их суммы равна сумме вероятностей этих событий.
Имеем:
\(P(A)=0,86x\),
\(P(B)=0,06\cdot(1-x)\),
\(P(A+B)=P(A)+P(B)=0,86x+0,06(1-x)=0,1\).
Мы составили уравнение, решив которое, найдем вероятность \(x\).
\(x=0,05\).
Что такое вероятность \(x\)? Это вероятность того, что пациент, пришедший к доктору, действительно болен. Здесь множество возможных исходов - это количество всех пациентов, пришедших к доктору.
Нам же нужно найти вероятность z того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание. Вероятность этого события равна \(0,05\cdot0,86\) (пациент болен и ПЦР-тест выявил заболевание, произведение событий). С другой стороны, эта вероятность равна \(0,1\cdot z\) (у пациента положительный результат ПЦР-теста, и при выполнении этого условия он действительно болен).
Получим:\(0,05 \cdot 0,86=0,1\cdot z\), отсюда \(z=0,43\).
Ответ: 0,43
14. Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.
Решение:
Рассмотрим возможные варианты. Игральную кость могли бросить:
1 раз, выпало 4 очка. Вероятность этого события равна \(\frac{1}{6}\) (1 благоприятный исход из 6 возможных). При этом, если получили 4 очка, кость больше не бросаем.
2 раза, выпало 3 и 1 или 1 и 3 или 2 и 2. При этом, если получили 4 очка, больше не бросаем кость. Для 2 бросков: всего 36 возможны исходов, из них 3 благоприятных, вероятность получить 4 очка равна \(\frac{3}{36}\).
3 раза, выпало 1, 1, 2 или 1, 2, 1 или 2, 1, 1. Если получили 4 очка – больше не бросаем кость. Для 3 бросков: всего \(6^3=216\) возможны исходов, из них 3 благоприятных, вероятность получить 4 очка равна \(\frac{3}{216}\).
4 раза, каждый раз по 1 очку. Вероятность этого события равна \(\frac{1}{6^4}\)
Вероятность получить 4 очка равна
\(P=\frac{1}{6}+\frac{3}{6^2}+\frac{3}{6^3}+\frac{1}{6^4}=\frac{1}{6}(1+\frac{3}{6}+\frac{3}{6^2}+\frac{1}{6^3})=\frac{1}{6}(1+\frac{1}{6})^3=\frac{1}{6}\cdot \frac{7^3}{6^3}=\frac{7^3}{6^4}\).
Воспользуемся формулой условной вероятности.
Пусть \(P_1\) - вероятность получить 4 очка, сделав 1 бросок; \(P_1=\frac{1}{6}\)(для одного броска: 6 возможных исходов, 1 благоприятный);
\(P\) — вероятность получить 4 очка с одной или нескольких попыток, \(P=\frac{7^3}{6^4}\).
\(P_2\) — вероятность, что при этом был сделан только один бросок;
\(P_1=P\cdot P_2\)
\(\frac{1}{6}=\frac{1}{6}\cdot\frac{7^3}{6^3}\cdot P_2\)
\(P_2=\frac{6^3}{7^3}=\frac{216}{343} \approx 0,63\)
Ответ: 0,63
15. Первый игральный кубик обычный, а на гранях второго кубика числа 5 и 6 встречаются по три раза. В остальном кубики одинаковые.
Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 5 и 6 очков. Какова вероятность того, что бросали второй кубик?
Решение:
1) Предположим, что бросали первый кубик. Мы выбрали этот кубик случайно, с вероятностью Тогда вероятность того, что в любом порядке выпали 5 и 6 очков, равна \(\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}=\frac{1}{18}\).
2) Теперь предположим, что бросали второй кубик, который мы тоже выбрали случайно, с вероятностью \(\frac{1}{2}\).
Вероятность того, что на этом кубике выпали 5 и 6 очков (или 6 и 5), равна \(\frac{3}{6}\cdot \frac{3}{6}+\frac{3}{6}\cdot \frac{3}{6}=\frac{1}{2}\).
Таким образом, вероятность равна \(\frac{\frac{1}{2}}{\frac{1}{18}+\frac{1}{2}}=\frac{9}{1+9}=0,9\).
Ответ: 0,9.
16. На рисунке показано дерево некоторого случайного эксперимента. Событию \(A\) благоприятствуют элементарные события \(a\), \(b\) и \(c\), а событию \(B\) благоприятствуют элементарные события \(b\), \(c\) и \(d\). Найдите \(P(A|B)\) — условную вероятность события \(A\) при условии \(B\).
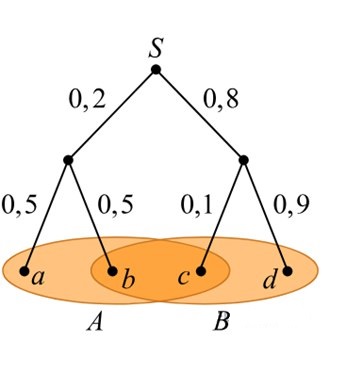
Решение:
По рисунку находим вероятности элементарных событий \(a\), \(b\) и \(c\).
\(P(a)=P(b)=0,2\cdot0,5=0,1\).
\(P(c)=0,8\cdot0,1=0,08\).
\(P(d)=0,8\cdot0,9=0,72\).
Вероятность события А равна сумме вероятностей событий \(a\), \(b\) и \(c\).
\(P(A)=P(a)+P(b)+P(c)=0,1+0,1+0,08=0,28\).
Вероятность события B равна сумме вероятностей событий \(b\), \(c\) и \(d\).
\(P(B)=P(b)+P(c)+P(d)=0,1+0,08+0,72=0,9\).
Вероятность произведения событий \(A\) и \(B\) равна сумме вероятностей событий \(b\) и \(c\)
\(P(AB)=P(b)+P(c)=0,1+0,08=0,18\).
По формуле условной вероятности
\(P(AB)=\frac{P(AB)}{P(B)}=\frac{0,18}{0,9}=0,2\).
Ответ: 0,2.
17. На диаграмме Эйлера показаны события \(A\) и \(B\) в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите \(P(B|A)\) — условную вероятность события \(B\) при условии \(A\).
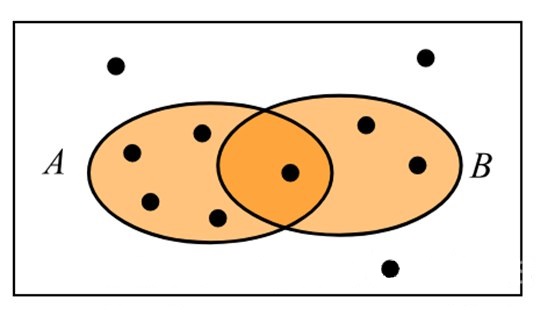
Решение:
На диаграмме нарисована не картошка, а круги Эйлера. Другими словами, показаны 2 множества, \(A\) и \(B\), у которых есть общий элемент. И еще 3 элемента не принадлежат ни множеству \(A\), ни множеству \(B\).
Согласно диаграмме,
\(P(A)=\frac{5}{10}\),
\(P(B)=\frac{3}{10}\),
\(P(AB)=\frac{1}{10}\).
По формуле условной вероятности:
\(P(B|A)=\frac{P(AB)}{P(A)}=\frac{1\cdot 10}{10\cdot 5}=\frac{1}{5}=0,2\).
Ответ: 0,2.
