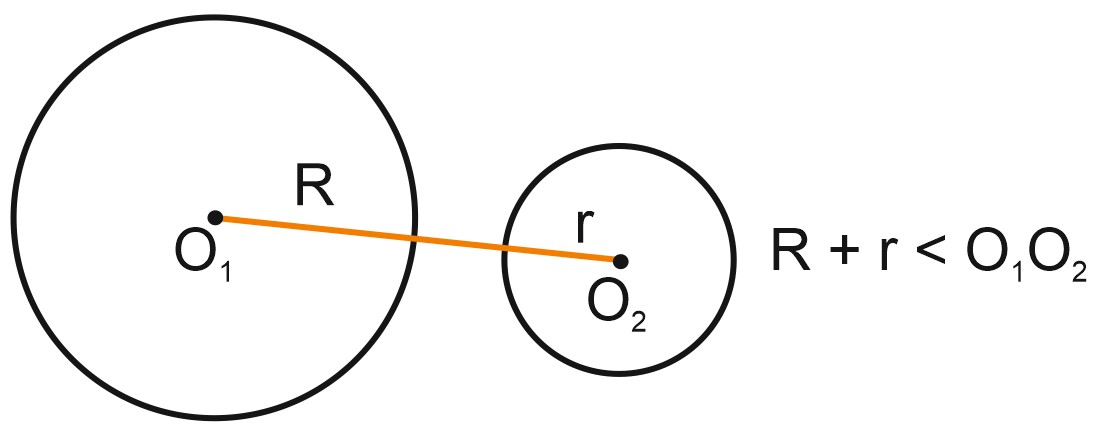Две окружности могут не иметь общих точек. Это происходит, если расстояние между центрами окружностей больше, чем сумма их радиусов.
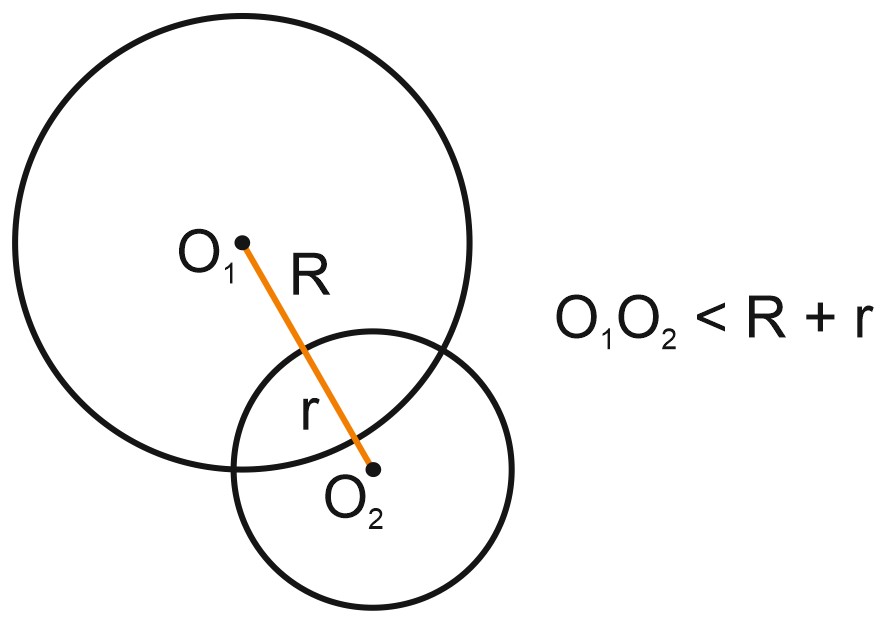
Две окружности могут пересекаться. В этом случае расстояние между центрами окружностей меньше, чем сумма их радиусов.
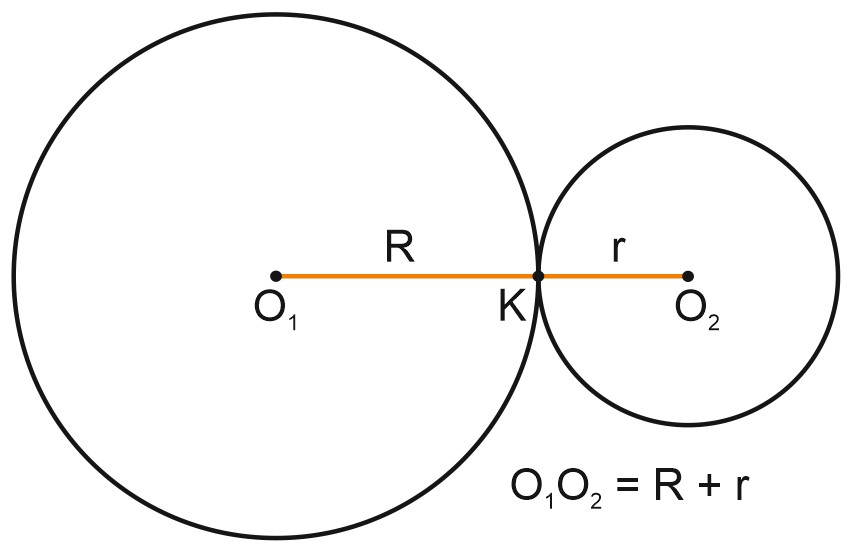
Самые интересные случаи – если расстояние между центрами окружностей равно сумме их радиусов. Тогда окружности касаются друг друга. У них единственная общая точка.
В этом случае точка касания окружностей лежит на отрезке, соединяющем их центры, \(O_{1}K+O_{2}K=O_{1}O_{2}\).
А расстояние между центрами \(O_{1}O_{2}=R+r\).
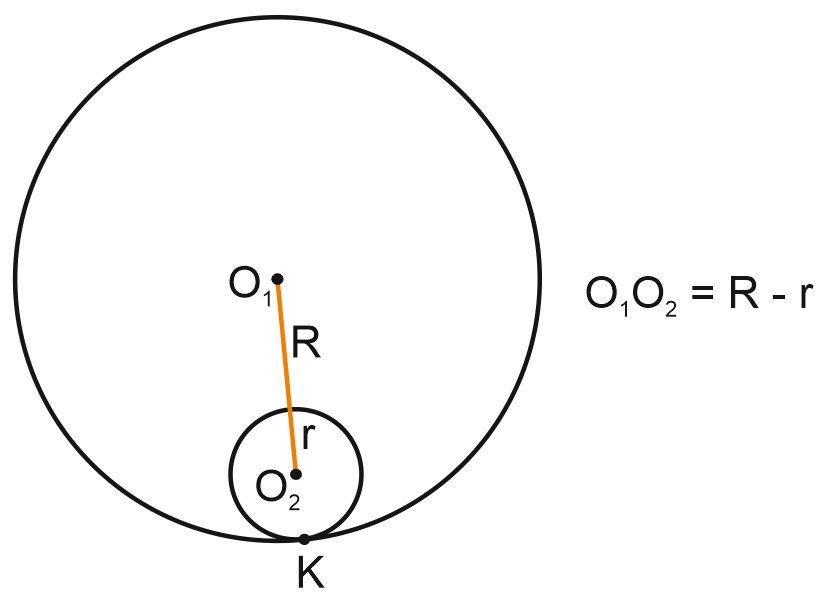
В задачах ЕГЭ может встретиться еще один случай: окружности касаются, но не внешним образом, а внутренним, одна в другой.
В таком случае расстояние между центрами окружностей равно разности их радиусов, \(O_{1}O_{2}=R-r\).
Точка касания также лежит на линии центров, \(O_{1}K-O_{2}K=O_{1}O_{2}\).