ОГЭ по Математике Вариант 2

1. Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Площадь листа формата А0 равна 1 кв.м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два листа формата А1. Если так же лист А1 разрезать пополам, получаются два листа формата А2 и так далее.

Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится. На практике размеры листа округляют до целого числа миллиметров.

В таблице 1 даны размеры листов бумаги четырех размеров: от А3 до А6.

Порядковые номера	Ширина (мм)	Длина (мм)
1	105	148
2	210	297
3	297	420
4	148	210

Для листов бумаги форматов А3, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырех цифр.

Форматы бумаги	А3	А4	А5	А6
Порядковые номера

Посмотреть ответ. Посмотреть решение.

2. Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Площадь листа формата А0 равна 1 кв.м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два листа формата А1. Если так же лист А1 разрезать пополам, получаются два листа формата А2 и так далее.

Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится. На практике размеры листа округляют до целого числа миллиметров.

В таблице 1 даны размеры листов бумаги четырех размеров: от А3 до А6.

Порядковые номера	Ширина (мм)	Длина (мм)
1	105	148
2	210	297
3	297	420
4	148	210

Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А0?

Посмотреть ответ. Посмотреть решение.

3. Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Площадь листа формата А0 равна 1 кв.м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два листа формата А1. Если так же лист А1 разрезать пополам, получаются два листа формата А2 и так далее.

Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится. На практике размеры листа округляют до целого числа миллиметров.

В таблице 1 даны размеры листов бумаги четырех размеров: от А3 до А6.

Порядковые номера	Ширина (мм)	Длина (мм)
1	105	148
2	210	297
3	297	420
4	148	210

Найдите длину большей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.

Посмотреть ответ. Посмотреть решение.

4. Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Площадь листа формата А0 равна 1 кв.м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два листа формата А1. Если так же лист А1 разрезать пополам, получаются два листа формата А2 и так далее.

Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится. На практике размеры листа округляют до целого числа миллиметров.

В таблице 1 даны размеры листов бумаги четырех размеров: от А3 до А6.

Порядковые номера	Ширина (мм)	Длина (мм)
1	105	148
2	210	297
3	297	420
4	148	210

Найдите площадь листа бумаги формата А3. Ответ дайте в квадратных сантиметрах.

Посмотреть ответ. Посмотреть решение.

5. Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Площадь листа формата А0 равна 1 кв.м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два листа формата А1. Если так же лист А1 разрезать пополам, получаются два листа формата А2 и так далее.

Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится. На практике размеры листа округляют до целого числа миллиметров.

В таблице 1 даны размеры листов бумаги четырех размеров: от А3 до А6.

Порядковые номера	Ширина (мм)	Длина (мм)
1	105	148
2	210	297
3	297	420
4	148	210

Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площадью 1 кв.м равна 80 г. Ответ дайте в граммах.

Посмотреть ответ. Посмотреть решение.

6. Найдите значение выражения \((4,9\cdot10^{-3})(4\cdot10^{-2})\).

Посмотреть ответ. Посмотреть решение.

7. Одна из точек, отмеченных на координатной прямой, соответствует числу \(\sqrt{14}\). Какая это точка?

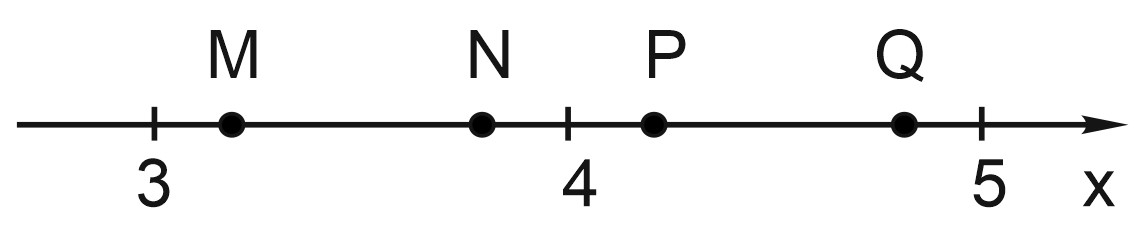
1) точка M

2) точка N

3) точка P

4) точка Q

Посмотреть ответ. Посмотреть решение.

8. В какое из следующих выражений можно преобразовать дробь \(\frac{c^{-6}\cdot c^3}{c^{-2}}\).

1) \(c^{-1}\) 

2) \(c^{-5}\) 

3) \(c^6\) 

4) \(c^0\)

Посмотреть ответ. Посмотреть решение.

9. Решите уравнение \((x+2)^2=(x-4)^2\).

Посмотреть ответ. Посмотреть решение.

10. Рэпер Клим готовится выступить на концерте. Он считает, что чем позже выступает артист на концерте, тем он круче. Порядок выступлений определяется случайным образом. С какой вероятностью Клим выступит после своих основных соперников: Гоги и Алекса? Ответ округлите до сотых. 

Посмотреть ответ. Посмотреть решение.

11. На рисунках изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.

Графики

Коэффициенты:

1) k<0, b>0

2) k<0, b<0  3) k>0, b>0

В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А

Б

В

Посмотреть ответ. Посмотреть решение.

12. Период колебания математического маятника (в секундах) приближенно можно вычислить по формуле \(T=2\sqrt{l}\), где \(l\) — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.

Посмотреть ответ. Посмотреть решение.

13. Решите неравенстов: \(x^2-17x+72\geq 0\).

На каком из рисунков изображено множество его решений?

В ответе укажите номер правильного варианта.

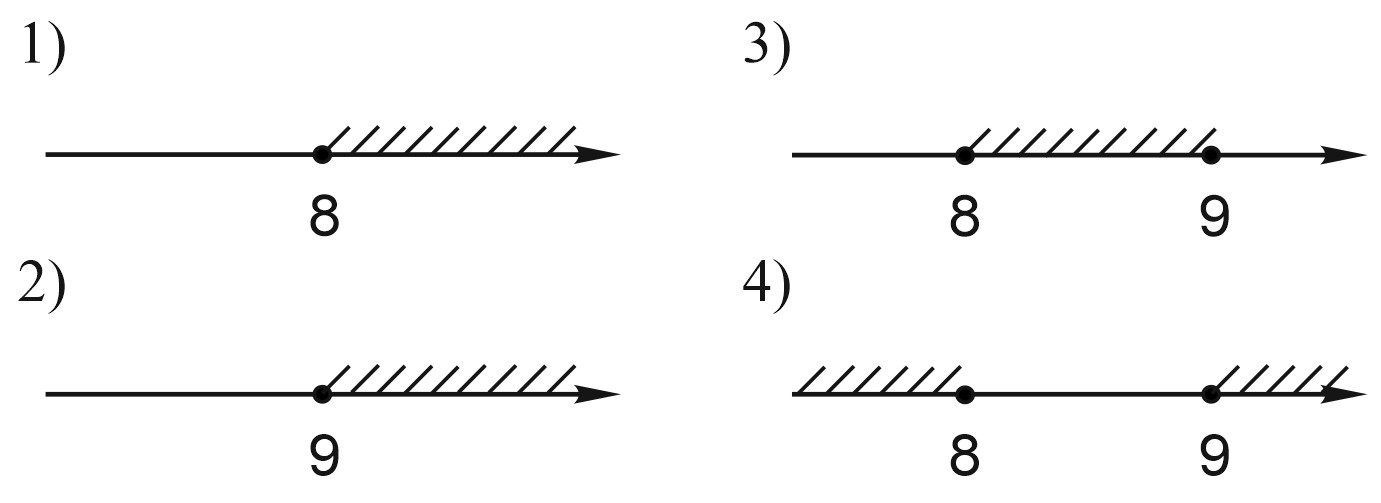
Посмотреть ответ. Посмотреть решение.

14. В ходе бета-распада радиоактивного изотопа А каждые 9 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 640 мг. Найдите массу образовавшегося изотопа Б через 45 минут. Ответ дайте в миллиграммах.

Посмотреть ответ. Посмотреть решение.

15. На стороне BC прямоугольника ABCD, у которого AB=48 и AD=112, отмечена точка E так, что ∠EAB=45°. Найдите ED.

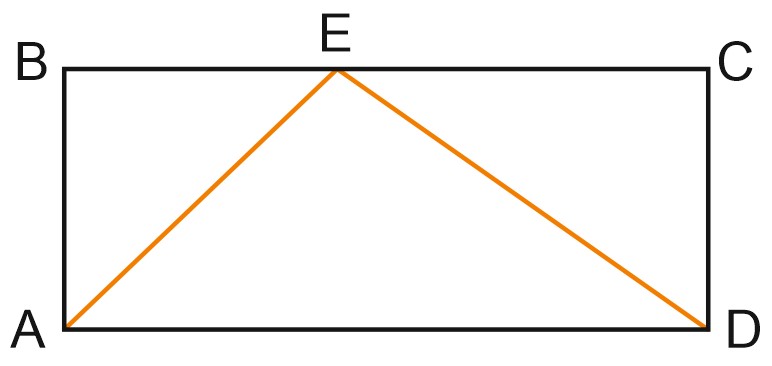
Посмотреть ответ. Посмотреть решение.

16. Отрезки AC и BD — диаметры окружности  с центром O. Угол ACB равен 56°. Найдите угол AOD. Ответ дайте в градусах.

Посмотреть ответ. Посмотреть решение.

17. Основания трапеции равны 6 и 10, одна из боковых сторон равна \(3\sqrt2\), а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.

Посмотреть ответ. Посмотреть решение.

18. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

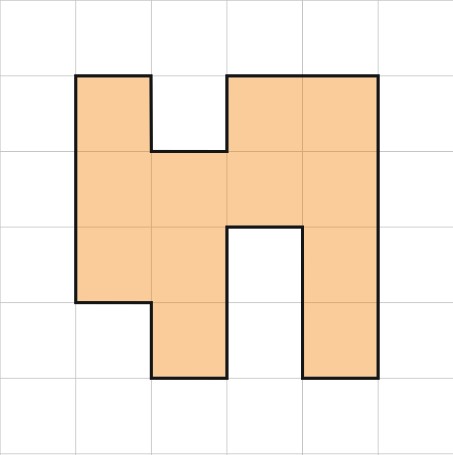
Посмотреть ответ. Посмотреть решение.

19. Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

Посмотреть ответ. Посмотреть решение.

20. Решите уравнение: \(-4x^2-7x+12=(x-2)^2\).

В ответе запишите корни в порядке возрастания, через точку с запятой ; без пробелов.

Посмотреть ответ. Посмотреть решение.

21. Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 2 часа, вернулись обратно через 6 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?

Посмотреть ответ. Посмотреть решение.

22. Постройте график функции \(y=\frac{(\sqrt{16-x^2})^2}{x+4}\) и найдите все значения \(a\), при которых прямая \(y=a\) имеет с графиком данной функции ровно одну общую точку. 

В ответе запишите наибольшее целое значение \(a\), удовлетворяющее этому условию.

Посмотреть ответ. Посмотреть решение.

23. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=14, DC=56, AC=40.

Посмотреть ответ. Посмотреть решение.

24. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник.

Каким из полезных фактов вы пользовались при доказательстве? Выберите правильный вариант. В ответе запишите (без точки) номер этого варианта, например: 1 

1) Касательная перпендикулярна радиусу, проведенному в точку касания.

2) Если четырехугольник описан вокруг окружности, то суммы длин его противоположных сторон равны.

3) Сумма односторонних углов равна 180 градусам.

Посмотреть ответ. Посмотреть решение.

25. Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=5 и MB=10. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.

Посмотреть ответ. Посмотреть решение.