Иррациональные неравенства

Так называются неравенства, содержащие знак корня.

В решении иррациональных неравенств главное – логика и внимательность.

И конечно, надо повторить следующие темы:

1) Арифметический квадратный корень.

2) Решение неравенств. Основные ошибки и полезные лайфхаки.

Напоминаем, что решение лучше всего записывать в виде цепочки равносильных переходов.

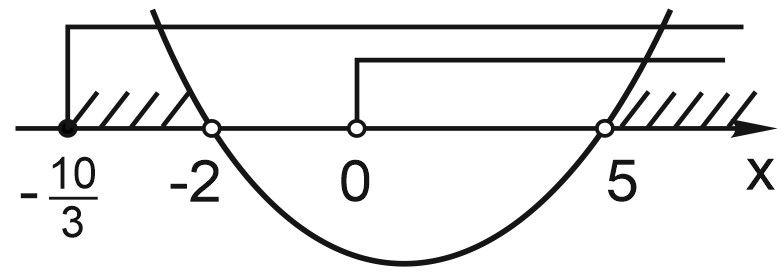
1. Решите неравенство:  \(x> \sqrt{3x+10}.\)

Правая часть неравенства неотрицательна: \(\sqrt{3x+10}\geq 0\) (по определению корня квадратного).

Поскольку \(x> \sqrt{3x+10}\), левая часть положительна: \(x> 0.\)

Выражение под корнем должно быть неотрицательным. Неравенство равносильно системе:

\(\left\{\begin{matrix}
x> 0, \\3x+10\geq 0,
\\x^{2}> 3x+10;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
x> 0, \\3x+10\geq 0,
\\x^{2}-3x-10> 0;
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x> 0, \\x\geq -\displaystyle\frac{10}{3},
\\(x-5)(x+2)> 0.
\end{matrix}\right.\)

Ответ: \((5; +\infty ).\)

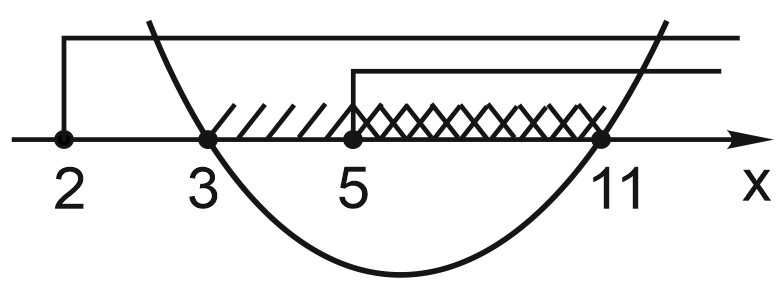
2. Решите неравенство: \(\sqrt{4x-8}\geq x-5\).

Как вы думаете – это неравенство такое же, как предыдущее, или отличается от него? Ведь здесь правая часть может быть и положительной, и отрицательной, и равной нулю. И надо рассмотреть все эти случаи.

1) Пусть правая часть неравенства неотрицательна. И левая тоже неотрицательна (по определению арифметического квадратного корня). И подкоренное выражение неотрицательно. Значит, при \(x-5\geq 0\) обе части неравенства можно возвести в квадрат.

Получим:

\(\left\{\begin{matrix}
x-5\geq 0, \\4x-8\geq 0,
\\4x-8\geq (x-5)^{2};
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\geq 5, \\x\geq 2,
\\x^{2}-14x+33\leq 0.
\end{matrix}\right.\)

Разложим выражение \(x^{2}-14x+33\) на множители. Корни уравнения \(x^{2}-14x+33=0\) – это \(x=3\) и \(x=11\).

Получаем систему:

\(\left\{\begin{matrix}
x\geq 5, \\x\geq 2,
\\(x-3)(x-11)\leq 0;
\end{matrix}\right.\Leftrightarrow 5\leq x\leq 11.\)

2) Пусть теперь правая часть неравенства отрицательна. Если \(x-5< 0\), то неравенство выполняется. В самом деле, \(\sqrt{a}\geq 0\) по определению. Значит, \(\sqrt{4x-8}\geq 0.\)

Нам нужно только, чтобы подкоренное выражение было неотрицательно: \(4x-8\geq 0\).

Получим:

\(\left\{\begin{matrix}
x-5< 0, \\4x-8\geq 0;
\end{matrix}\right.\Leftrightarrow 2\leq x< 5.\)

Объединим полученные интервалы и запишем ответ.

Ответ: \(\left [ 2; 11 \right ]\).

3. Решите неравенство: \(\sqrt{x-1}< 3-x.\)

Решение:

\(\sqrt{x-1}< 3-x \Leftrightarrow \left\{\begin{matrix}
x-1\geq 0, \\3-x\geq 0,
\\(\sqrt{x-1})^{2}< (3-x)^{2};
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
x\geq 1, \\x\leq 3,
\\x-1< 9+x^{2}-6x;
\end{matrix}\right. \Leftrightarrow \)

\(\Leftrightarrow \left\{\begin{matrix}
x\geq 1, \\x\leq 3,
\\-x^{2}+7x-10< 0; \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x\geq 1, \\x\leq 3,  \\x^{2}-7x+10> 0;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
x\geq 1, \\x\leq 3,
\\(x-2)(x-5)> 0.
\end{matrix}\right.\)

Ответ: \( x \in [1; 2).\)

4. Решите неравенство: \(\sqrt{x+1}>  x-2.\)

Решение:

\(\sqrt{x+1}> x-2\Leftrightarrow \left\{\begin{matrix}
x+1\geq 0, \\
\left[\begin{matrix}
\left\{\begin{matrix}
x-2\geq 0, \\x+1> (x-2)^{2},
\end{matrix}\right.
\\x-2< 0; \end{matrix}\right.  \end{matrix}\right. \Leftrightarrow  \left\{\begin{matrix} x\geq -1, \\   \left[\begin{matrix} \left\{\begin{matrix} x\geq 2, \\x+1> x^{2}-4x+4,
\end{matrix}\right.
\\x< 2;
\end{matrix}\right.
\end{matrix}\right. \Leftrightarrow\)

\(\Leftrightarrow \left\{\begin{matrix}
x\geq -1, \\
\left[\begin{matrix}
\left\{\begin{matrix}
x\geq 2, \\x^{2}-5x+3< 0,
\end{matrix}\right.
\\x< 2;
\end{matrix}\right.
\end{matrix}\right. \Leftrightarrow
\left\{\begin{matrix}
x\geq -1, \\
\left[\begin{matrix}
\left\{\begin{matrix}
x\geq 2, \\\left (x-\displaystyle \frac{5+\sqrt{13}}{2}\right )\left (x-\displaystyle \frac{5-\sqrt{13}}{2}\right )< 0,
\end{matrix}\right.
\\x< 2;
\end{matrix}\right.
\end{matrix}\right. \Leftrightarrow\)

\(\Leftrightarrow \left[\begin{matrix}
-1\leq x< 2,\\\left\{\begin{matrix}
x\geq 2, \\\left (x-\displaystyle \frac{5+\sqrt{13}}{2}\right )\left (x-\displaystyle \frac{5-\sqrt{13}}{2}\right )< 0;
\end{matrix}\right.
\end{matrix}\right.\)

\(\displaystyle \frac{5+\sqrt{9}}{2}< \frac{5+\sqrt{13}}{2}< \frac{5+\sqrt{16}}{2};\)

\(4< \displaystyle \frac{5+\sqrt{13}}{2}< 4,5;\)

\(\displaystyle \frac{5-\sqrt{16}}{2}< \frac{5-\sqrt{13}}{2}< \frac{5-\sqrt{9}}{2};\)

\(0,5< \displaystyle \frac{5-\sqrt{13}}{2}< 1.\)

Ответ: \(x\in \left [-1; \displaystyle \frac{5+\sqrt{13}}{2}\right ).\)

5. Решите неравенство: \(\displaystyle \frac{1}{8x^{2}+6x}\geq \frac{1}{\sqrt{8x^{2}+6x+1}-1}.\)

Решение:

Сделаем замену \(\sqrt{8x^{2}+6x+1}=t, \;t\geq 0\), тогда \(8x^{2}+6x=t^{2}-1 \)

\(\left\{\begin{matrix}
\displaystyle \frac{1}{t^{2}-1}\geq \frac{1}{t-1}, \\t\geq 0;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
\displaystyle \frac{1}{(t-1)(t+1)}- \frac{1}{t-1}\geq 0, \\t\geq 0;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
\displaystyle \frac{1-t-1}{(t-1)(t+1)}\geq 0, \\t\geq 0;
\end{matrix}\right.\Leftrightarrow \)

\(\Leftrightarrow \left\{\begin{matrix}
\displaystyle \frac{t}{(t-1)(t+1)}\leq 0, \\t\geq 0;
\end{matrix}\right.\Leftrightarrow 0\leq t< 1.\)

\(0\leq \sqrt{8x^{2}+6x+1}< 1\Leftrightarrow \left\{\begin{matrix}
8x^{2}+6x+1\geq 0, \\\sqrt{8x^{2}+6x+1}< 1;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
8x^{2}+6x+1\geq 0, \\8x^{2}+6x+1< 1;
\end{matrix}\right.\Leftrightarrow \)

\(\Leftrightarrow \left\{\begin{matrix}
8x^{2}+6x+1\geq 0, \\8x^{2}+6x< 0;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
8x^{2}+6x+1\geq 0, \\x(4x+3)< 0;
\end{matrix}\right.\)

\(8x^{2}+6x+1=0;\)

\(D=36-32=4.\)

\(x_{1}=\displaystyle \frac{-6+2}{16}=-\frac{1}{4};\)

\(x_{2}=\displaystyle \frac{-6-2}{16}=-\frac{1}{2}.\)

\(\left\{\begin{matrix}
8x^{2}+6x+1\geq 0, \\x(4x+3)< 0;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
8\left (x+\displaystyle \frac{1}{2}\right )\left (x+\displaystyle \frac{1}{4}\right )\geq 0, \\x(4x+3)< 0;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
\left (x+\displaystyle \frac{1}{2}\right )\left (x+\displaystyle \frac{1}{4}\right )\geq  0, \\x(4x+3)< 0.
\end{matrix}\right.\)

Ответ: \(x \in \left (\displaystyle -\frac{3}{4};\;-\frac{1}{2} \right )\cup \left ( \displaystyle -\frac{1}{4} ;\;0\right ).\)

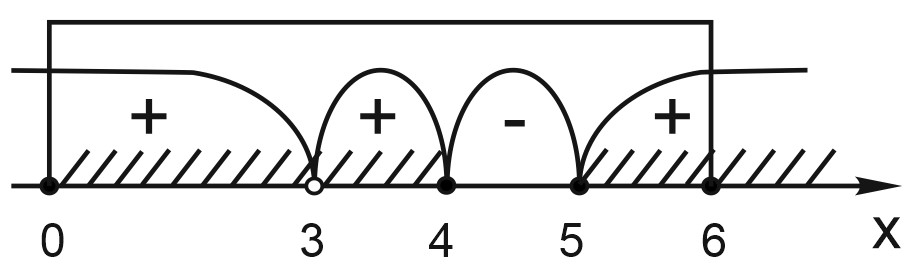
6. Решите неравенство \(\left (\displaystyle \frac{1}{x^{2}-7x+12} +\frac{x-4}{3-x}\right )\sqrt{6x-x^{2}}\leq 0.\)

Решение:

\(\left (\displaystyle \frac{1}{x^{2}-7x+12} +\frac{x-4}{3-x}\right )\sqrt{6x-x^{2}}\leq 0\Leftrightarrow \left\{\begin{matrix}
x^{2}-7x+12\neq 0,\\
x\neq 3,\\
6x-x^{2}\geq 0,\\
\left[
\begin{array}{ccc}
6x-x^{2}=0, \\
\displaystyle \frac{1}{x^{2}-7x+12}+\frac{x-4}{3-x} \leq 0; \\
\end{array}
\right.
\end{matrix}\right. \Leftrightarrow\)

\(\Leftrightarrow \left\{\begin{matrix}
x\neq 4,\\
x\neq 3,\\
6x-x^{2}\geq 0,\\
\left[
\begin{array}{ccc}
x=0, \\
x=6,\\
\displaystyle \frac{1}{\left ( x-3 \right )\left ( x-4 \right )}-\frac{x-4}{x-3} \leq 0; \\
\end{array}
\right.
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
x\neq 4,\\
x\neq 3,\\
x\left ( x-6 \right )\leq 0,\\
\left[
\begin{array}{ccc}
x=0, \\
x=6,\\
\displaystyle \frac{1-\left ( x-4 \right )^{2}}{\left ( x-3 \right )\left ( x-4 \right )} \leq 0;\\
\end{array}
\right.
\end{matrix}\right.\Leftrightarrow\)

\(\Leftrightarrow \left\{\begin{matrix}
x\neq 4,\\
x\neq 3,\\
x\left ( x-6 \right )\leq 0,\\
\left[
\begin{array}{ccc}
x=0, \\
x=6,\\
\displaystyle \frac{\left ( 1-x+4 \right )\left ( 1+x-4 \right )}{\left ( x-3 \right )\left ( x-4 \right )} \leq 0;\\
\end{array}
\right.
\end{matrix}\right.\Leftrightarrow
\left\{\begin{matrix}
x\neq 4,\\
x\neq 3,\\
x\left ( x-6 \right )\leq 0,\\
\left[
\begin{array}{ccc}
x=0, \\
x=6,\\
\displaystyle \frac{\left ( x-3 \right )\left ( x-5 \right )}{\left ( x-3 \right )\left ( x-4 \right )} \geq 0.\\
\end{array}
\right.
\end{matrix}\right.\)

Ответ: \(x \in [0; 3)\cup (3; 4)\cup [5; 6].\)