Еще один тип задач ЕГЭ на числа и их свойства. В них применяются известные вам приемы, такие как метод «Оценка плюс пример».
Главное - не забыть нарисовать сам круг, на котором вы расставляете числа. У каждого числа на круге есть соседи и слева, и справа.
1. По кругу в некотором порядке по одному разу написаны числа от \(9\) до \(18\). Для каждой из десяти пар соседних чисел нашли их наибольший общий делитель.
а) Могло ли получиться так, что все наибольшие общие делители равны \(1\)?
б) Могло ли получиться так, что все наибольшие общие делители попарно различны?
в) Какое наибольшее количество попарно различных наибольших общих делителей могло при этом получиться?
Решение:
Заметим, что среди наших чисел есть \(3\) простых числа. Это \(11\), \(13\) и \(17\).
Приведем пример, когда все наибольшие общие делители равны \(1\).
Ваш пример может быть другим. Найти такой пример легко.
б) Выпишем в табличку делители чисел \(9, 10, ..., 18.\)
| Число | Делители |
| \(9\) | \(1, 3, 9\) |
| \(10\) | \(1, 2, 5, 10\) |
| \(11\) | \(1, 11\) |
| \(12\) | \(1, 2, 3, 4, 6, 12\) |
| \(13\) | \(1, 13\) |
| \(14\) | \(1, 2, 7, 14\) |
| \(15\) | \(1, 3, 5, 15\) |
| \(16\) | \(1, 2, 4, 8, 16\) |
| \(17\) | \(1, 17\) |
| \(18\) | \(1, 2, 3, 6, 9, 18\) |
Предположим, что все наибольшие общие делители наших десяти чисел попарно различны. Поскольку таких делителей \(10\), а натуральных однозначных чисел всего \(9\), среди этих делителей найдется двузначное число. Если два различных числа делятся на какое-либо двузначное число, то хотя бы одно из них больше \(20\). Но таких чисел по условию нет. Мы получили противоречие, и \(10\) различных наибольших общих делителей у чисел на круге быть не может.
в) Посмотрим на нашу таблицу. Поскольку число \(10\) не может быть наибольшим общим делителем ни для каких двух чисел на круге (смотреть пункт (б)), количество попарно различных наибольших общих делителей не больше девяти, причем максимальный НОД равен \(9\).
Числа \(7\) и \(8\) не являются наибольшими общими делителями ни для одной пары чисел, так как на \(7\) делится только число \(14\), а на \(8\) - только \(16\). Значит, количество различных наибольших общих делителей не более семи.
Мы сделали оценку количества наибольших общих делителей. Приведем пример, когда их ровно \(7\). Эти наибольшие общие делители равны \(1, 2, 3, 4, 5, 6\) и \(9.\)
Ответ: а) Да; б) Нет; в) \(7\).
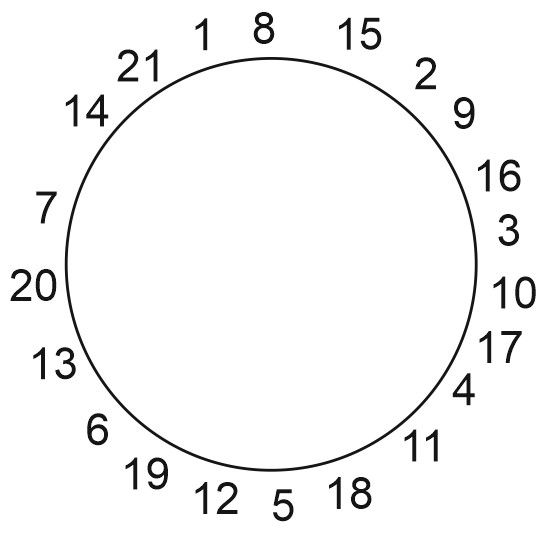
2. На окружности некоторым образом расставили натуральные числа от \(1\) до \(21\) (каждое число поставлено по одному разу). Затем для каждой пары соседних чисел нашли разность большего и меньшего.
а) Могли ли все полученные разности быть не меньше \(11\)?
б) Могли ли все полученные разности быть не меньше \(10\)?
в) Помимо полученных разностей, для каждой пары чисел, стоящих через одно, нашли разность большего и меньшего. Для какого наибольшего целого числа \(k\) можно так расставить числа, чтобы все разности были не меньше \(k\).
Решение:
а) Выпишем наши числа в ряд:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21.
Число \(11\) находится ровно посередине этой последовательности чисел. Модуль разности числа \(1\) и любого другого из оставшихся чисел не больше \(10\). Как бы мы ни расставили числа на окружности, все разности соседних чисел не могут быть больше \(11\) или равны \(11\).
б) Да, это возможно. Вот пример:
1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 6, 17, 7, 18, 8, 19, 9, 20, 10, 21, 11.
Легко видеть, что любое число на окружности здесь отличается от соседнего не меньше чем на \(10\).
в) Еще раз выпишем наши числа в ряд:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21.
Всего их \(21, 21=3\cdot 7\). Разобьем числа на три группы по \(7\) чисел.
1 группа: \(1, 2, 3, 4, 5, 6, 7;\)
2 группа: \(8, 9, 10, 11, 12, 13, 14;\)
3 группа: \(15, 16, 17, 18, 19, 20, 21.\)
Любые два числа из первой группы отличаются друг от друга не больше, чем на \(6\). Если числа из первой группы оказались на окружности рядом (или через одно), то их разность не больше \(6\).
Расставим числа на окружность так, что каждое третье число будет из первой группы.
Куда бы мы ни поставили число \(8\) - рядом с ним или через одно от него будет находиться число из первой группы. Тогда одна из соответствующих разностей не больше \(6\). Значит, все разности не могут быть равны \(7\) или быть больше \(7\).
Значит, \(k \leq 6. \)
Приведем пример, когда \(k=6.\)
Сначала расставим числа из первой группы (от \(1\) до \(7\)), оставив между каждыми из них два свободных места. Затем числа из второй группы и из третьей:
Получили, что наибольшее значение \(k\) равно \(6\).
Ответ: а) Нет; б) Да; в) \(6\).
3. По кругу расставлены \(N\) чисел так, что сумма трех последовательных чисел не делится на \(3\), а сумма четырех последовательных делится на \(3\).
а) Может ли \(N\) быть равно \(240\)?
б) Может ли \(N\) быть равно \(219\)?
в) Найдите наибольшее \(N\), если числа различны и каждое меньше \(340\).
Решение:
а) Да, может \(N=240\).
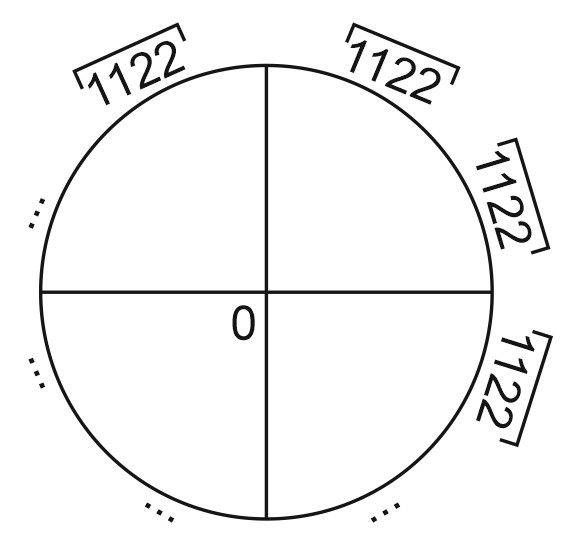
Например, по кругу расположены \(60\) четверок вида \(1, 1, 2, 2\) или \(1, 2, 1, 2.\)
Сумма чисел в каждой тройке не делится на \(3\), а в каждой четверке делится на \(3\).
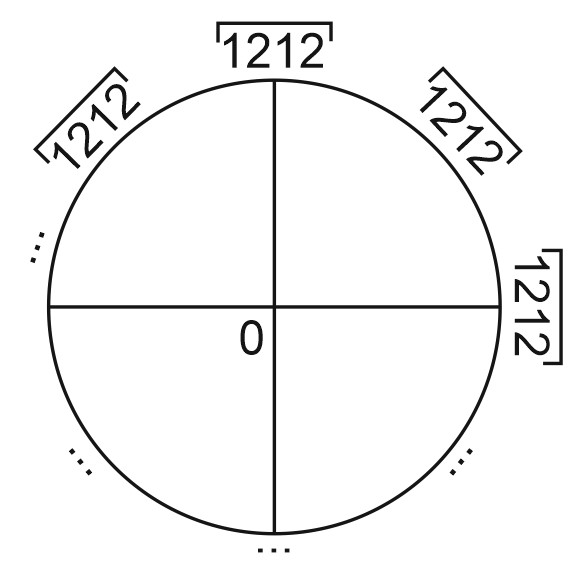
Возможен и такой вариант:
И в том, и в другом случае мы не ставим подряд три единицы или три двойки.
б) Посмотрим, какие вообще числа могут находиться на круге.
Пусть \(a, b, c\) и \(d\) – последовательные числа на круге, такие что \(a + b + c\) - не делится на \(3\). Тогда \(a + b + c\) при делении на \(3\) дает остаток \(1\) или \(2\).
Получим совокупность:
\(\left[\begin{matrix}
a+b+c=3n+1,\\a+b+c=3n+2,
\end{matrix}\right.\) где \(n = 0, 1, 2, \dots .\)
Сумма \(a + b + c + d\) делится на \(3\), тогда \(a + b + c + d = 3k,\) где \(k = 2, 3, \dots \)
Получаем систему: \(\left\{\begin{matrix}
\left[\begin{matrix}
a+b+c=3n+1,\; \; \; \; (1) \\a+b+c=3n+2,\; \; \; \; (2)
\end{matrix}\right. \\a+b+c+d=3k. \; \; \; \; \; \; \;(3)
\end{matrix}\right.\)
Если из уравнения (3) вычесть уравнение (1), то получим \(d\ =\ 3k-3n-1\) – это означает, что при делении числа \(d\) на \(3\) получается остаток \(2\).
Если из уравнения (3) вычесть уравнение (2), то получим \(d\ =\ 3k-3n-2\) – это означает, что при делении числа \(d\) на \(3\) получается остаток \(1\).
Значит, число \(d\) при делении на \(3\) дает остаток \(1\) или \(2\).
Так как \(d\) – любое число на круге, то все числа на круге при делении на \(3\) дают остаток \(1\) или \(2\), то есть на круге все числа вида \(3m + 1\) или \(3m + 2\).
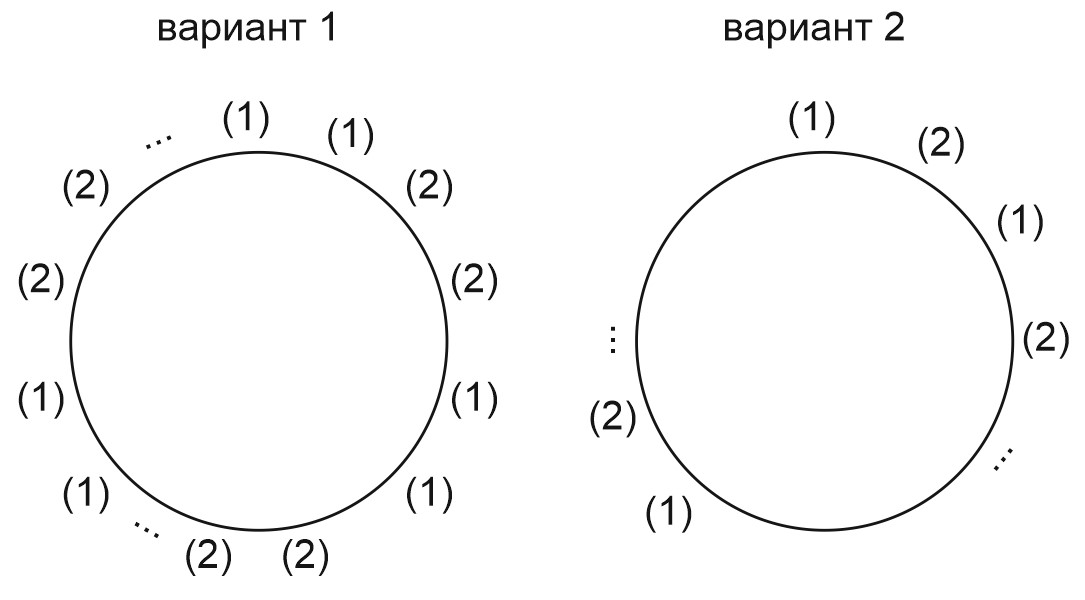
Так как по условию любые три подряд идущие числа не делятся на \(3\), значит, числа вида \(3m + 1\) не стоят три подряд, а стоят через одно или через два.
Аналогично, числа вида \(3m + 2\) не стоят три подряд, а стоят через одно или через два.
Обозначим числа, дающие при делении на \(3\) остаток \(1\), как \((1)\).
Числа, дающие при делении на \(3\) остаток \(2\), обозначим как \((2)\).
Получим варианты:
Других вариантов нет, так как сумма чисел в четверке должна быть кратна трем. Это значит, что если в ней \(2\) числа типа \((1)\), то должно быть и \(2\) числа типа \((2)\).
Предположим, что \(N = 129\).
\(129 = 128 + 1 = 32 \cdot 4+1\) то есть на круге \(32\) четверки чисел и еще одно число, причем это может быть либо число типа \((1)\), либо число типа \((2)\). Где же оно может быть расположено?
А вот нигде не может!
Рассмотрим сначала первый вариант. Пусть наше число типа \((1)\). Чтобы три числа типа \((1)\) не стояли подряд, мы можем поставить его только между двумя числами типа \((2)\). Но теперь вместе с тремя соседями слева или с тремя соседями справа оно дает четверку, в которой сумма не делится на \(3\).
Аналогично – если мы попытаемся добавить число типа \((2)\).
Так же и во втором варианте. Куда бы мы ни добавили новое число, вместе с тремя соседями слева или с тремя соседями справа оно дает четверку, в которой сумма не делится на \(3\). Значит, \(129\) чисел на круге быть не может.
в) Найдем наибольшее количество чисел на круге при условии, что все они различны и не превосходят \(340\). Мы сказали, что это должны быть числа, которые при делении на \(3\) дают остаток \(1\) или остаток \(2\). В пункте (б) мы определили, как они должны быть расположены на круге.
Мы сказали также, что если \(N\) – количество чисел на круге, то \(N\) делится на \(4\).
Пусть \(n = 4p\), то есть на круге \(p\) четверок чисел, в каждой из которых \(2\) числа типа \((1)\) и \(2\) числа типа \((2)\). Числа типа \((1)\), которые при делении на \(3\) дают остаток \(1\), - это \(1, 4, 7, 10 ...\)
Числа типа \((2)\), которые при делении на \(3\) дают остаток \(2\), - это \(2, 5, 8, 11 ...\)
Наибольшее число на круге – это число типа \((2)\), и по условию, оно меньше \(340\). Числа типа \((2)\) образуют арифметическую прогрессию
\(a_k=2+3\left(k-1\right).\)
Так как \(a_k< 340\), получим: \( 2 + 3 (k-1)< 340\) , отсюда \(k \leq 113.\)
Значит, на круге не более \(113\) чисел типа \((2)\). Но тогда и чисел типа \((1)\) столько же, то есть тоже не более \(113\). Всего на круге не более \(113 + 113 = 226\) чисел. Это оценка.
Приведем пример для \(226\) различных чисел на круге.
Ответ: а) Да; б) Нет; в) \(226\).