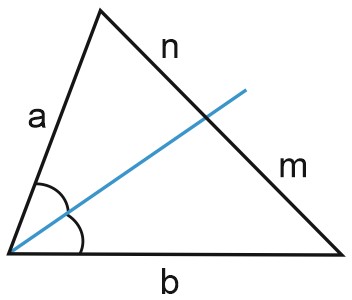
Биссектриса треугольника – это луч, исходящий из вершины треугольника и делящий угол пополам.
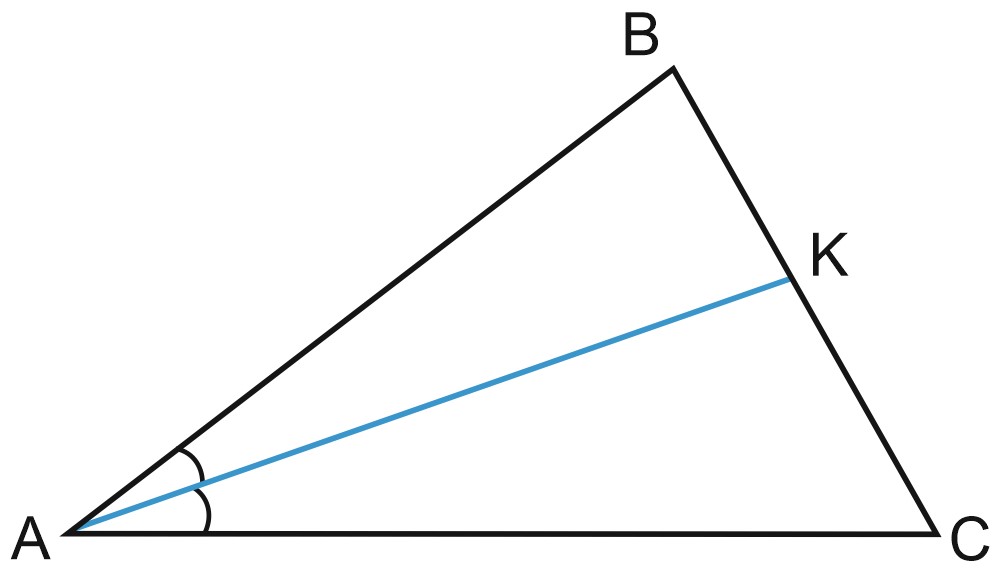
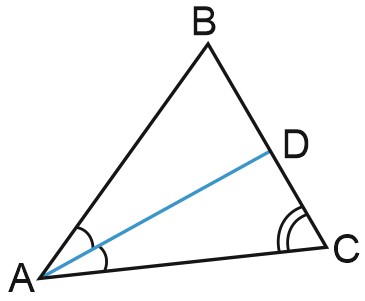
На рисунке \(AK\) – биссектриса угла \(A\) треугольника \(ABC\).
Есть и другое, неофициальное определение:
Биссектриса – это крыса, которая бегает по углам и делит угол по полам.
Высота может лежать снаружи треугольника. А биссектриса угла треугольника всегда лежит внутри него.
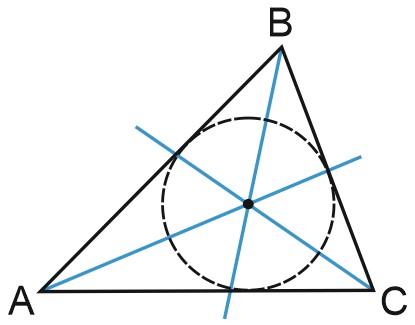
Три биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Докажем эту теорему.
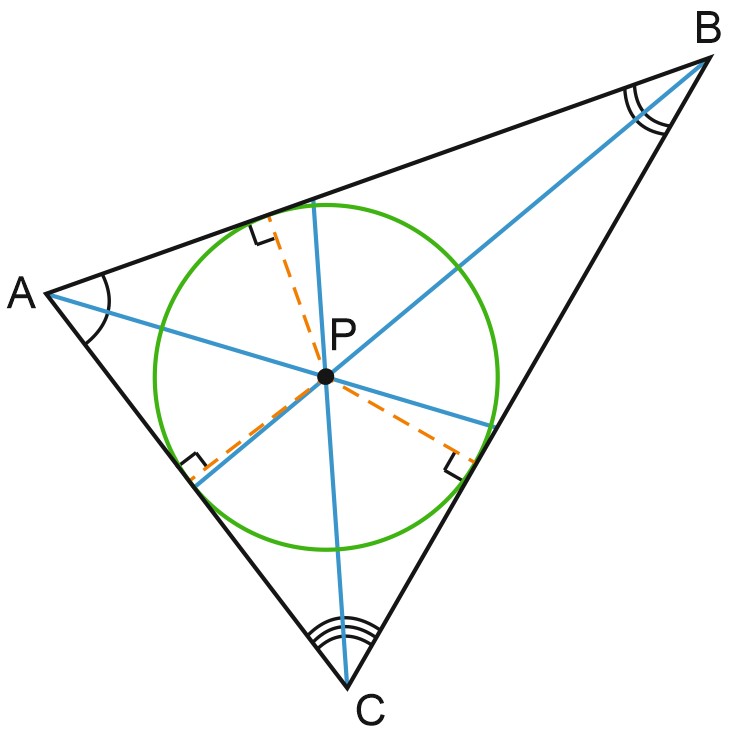
Пусть биссектрисы углов \(A\) и \(B\) треугольника пересекаются в точке \(P\). Тогда точка \(P\) равноудалена от сторон \(AB\) и \(AC\), поскольку лежит на биссектрисе угла \(A\), а также от сторон \(BC\) и \(BA\), поскольку лежит на биссектрисе угла \(B\). А это значит, что точка \(P\) равноудалена и от прямых \(AC\) и \(BC\), то есть лежит на биссектрисе угла \(C\).
Еще одно свойство биссектрисы часто применяется при решении задач.
Биссектриса угла треугольника делит противоположную сторону в отношении длин прилежащих сторон.
Доказательство этой теоремы здесь: Свойство биссектрисы треугольника.
Задача ЕГЭ по теме «Биссектрисы углов треугольника»
1. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Решение:
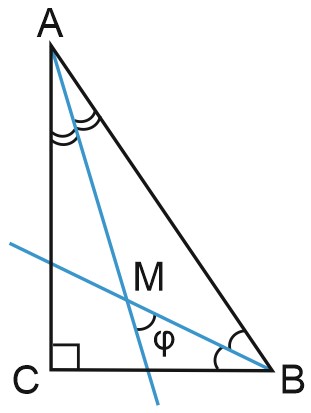
Пусть биссектрисы треугольника \(ABC\) (в котором угол \(C\) равен \(90 ^{\circ}\)) пересекаются в точке \(M\).
Рассмотрим треугольник \(ABM\).
\(\angle MAB=0,5\angle BAC; \)
\(\angle ABM=0,5\angle ABC,\) тогда \(\angle AMB=180^{\circ}-\angle MAB-\angle ABМ=180^{\circ}-0,5(\angle ABC+\angle BAC).\)
Острый угол медлу биссектрисами на рисунке обозначен \(\varphi \).
Угол \(\varphi \) смежный с углом \(AMB\), следовательно, \(\varphi =0,5(\angle ABC+\angle BAC).\)
Поскольку треугольник \(ABC\) – прямоугольный, то \(\angle ABC+\angle BAC=90 ^{\circ}.\)
Тогда \(\varphi =0,5(\angle ABC+\angle BAC)=90 ^{\circ}:2=45 ^{\circ}.\)
Ответ: 45.
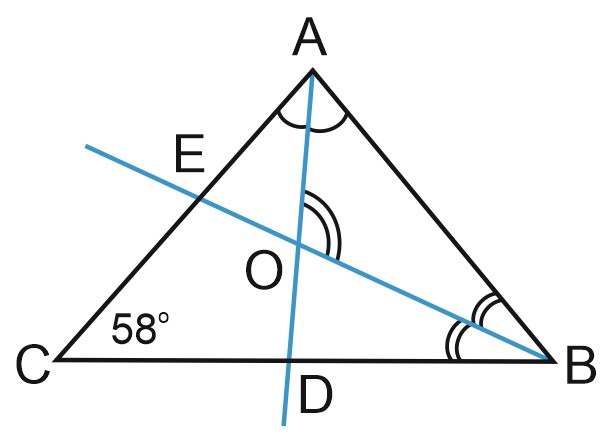
2. В треугольнике \(ABC\) угол \(C\) равен \(58 ^{\circ}, \; AD\) и \(BE\) – юиссектрисы, пересекающиеся в точке \(O\). Найдите
угол \(AOB\). Ответ дайте в градусах.
Решение:
Пусть в треугольнике \(ABC\) угол \(BAC\) равен \(A\), угол \(ABC\) равен \(B\).
Рассмотрим треугольник \(AOB\).
\(\angle OAB=\angle A; \)
\(\angle ABO=\angle B\), тогда \(\angle AOB=180^{\circ}-(\angle A+\angle B).\)
Из треугольника \(ABC\) получим, что \(\angle A+\angle B=180^{\circ}-58^{\circ}=122^{\circ}.\)
Тогда \(\angle AOB=180^{\circ}-(\angle A+\angle B)=180^{\circ} - 61^{\circ}=119^{\circ}.\)
Ответ: 119.
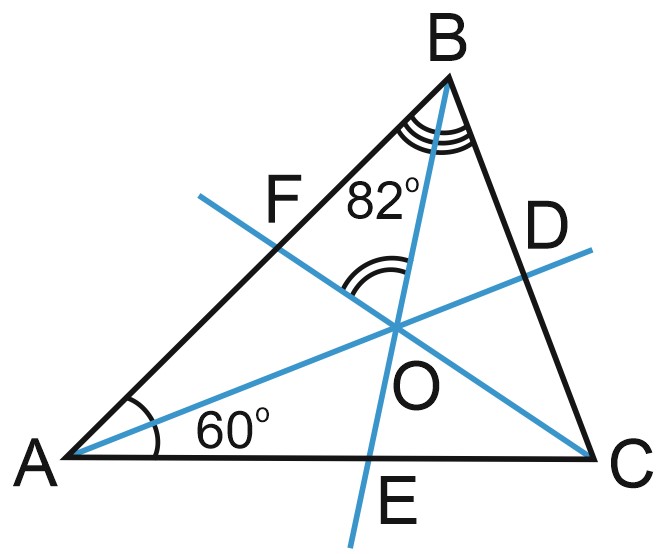
3. В треугольнике \(ABC\) угол \(A\) равен \(60 ^{\circ}\), угол \(B\) равен \(82 ^{\circ}\). \(AD, \; BD\) и \(CF\) — биссектрисы, пересекающиеся в точке \(A\). Найдите угол \(AOF\). Ответ дайте в градусах.
Решение:
Найдем угол \(ACB\). Он равен \(38 ^{\circ}\).
Тогда \(\angle ACF=\angle ACB =19^{\circ}.\)
Из треугольника \(ACF\) найдем угол \( \angle AFC=\angle ACB=19^{\circ}\). Он равен \(101^{\circ}.\)
Рассмотрим треугольник \(AOF\).
\(\angle AFO=101^{\circ}, \; \angle FAO\angle BAC=30^{\circ}.\)
Значит, \(\angle AOF=49^{\circ}\).
Ответ: 49.
4. В треугольнике \(ABC\) \(AD\) — биссектриса, угол \(C\) равен \(50 ^{\circ}\). Угол \(CAD\) равен \(28 ^{\circ}\). Найдите угол \(B\). Ответ дайте в градусах.
Решение:
Поскольку \(AD\) – биссектриса, то \(\angle A=2\cdot \angle CAD=2\cdot 28^{\circ }=56^{\circ }.\)
Сумма углов треугольника равна \(180^{\circ}\), следовательно,
\(\angle B=180^{\circ }- \angle A-\angle C=180^{\circ }-50^{\circ }-56^{\circ }=74^{\circ }.\)
Ответ: 74.
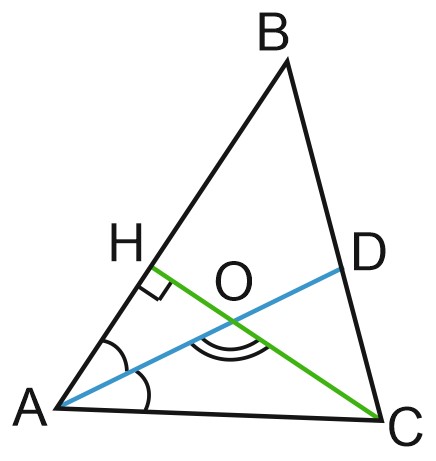
5. В треугольнике \(ABC\) \(CH\) – высота, \(AD\) – биссектриса, \(O\) – точка пересечения прямых \(CH\) и \(AD\), угол \(BAD\) равен \(26^{\circ}\). Найдите угол \(AOC\). Ответ дайте в градусах.
Решение:
Угол \(AOC\) – внешний в треугольнике \(AHO\), следовательно,
\(\angle AOC=\angle OAH+\angle AHO=26^{\circ }+90^{\circ }=116^{\circ }.\)
Ответ: 116.
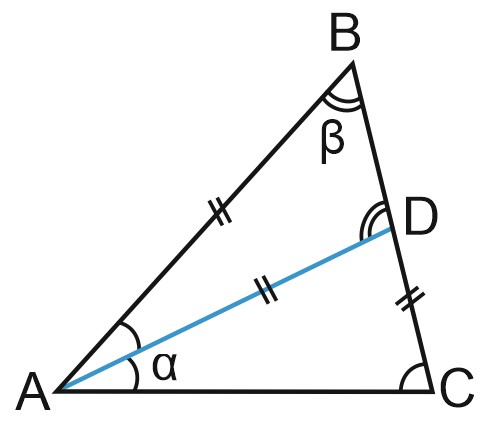
6. В треугольнике \(ABC\) проведена биссектриса \(AD\) и \(AB = AD = CD\). Найдите меньший угол
треугольника \(ABC\). Ответ дайте в градусах.
Решение:
\(AD = CD\), следовательно, треугольник \(ADC\) – равнобедренный и \(\angle DAC=\angle ACD=\alpha .\)
\(AD\) – биссектриса, следовательно, \(\angle BAD=\angle DAC=\alpha .\)
\(AB = AD\), следовательно, треугольник \(ABD\) – равнобедренный и \(\angle ABD=\angle ADB=\beta .\)
\(\angle ADB\) – внешний в треугольнике \(ADC\), следовательно, \(\angle ADB=\angle DAC+\angle ACD=2\alpha .\)
Таким образом, наименьшим углом треугольника \(ABC\) является \(\angle C=\alpha \), два других угла – в два раза больше.
Воспользуемся тем, что сумма углов треугольника \(ABC\) равна \(180^{\circ}\):
\(\angle A+\angle B+\angle C=2\alpha +2\alpha +\alpha =5\alpha =180^{\circ }\), откуда получаем: \(\alpha =180^{\circ }:5=36^{\circ }.\)
Наименьший угол треугольника \(ABC\) равен \(36^{\circ}\).
Ответ: 36.
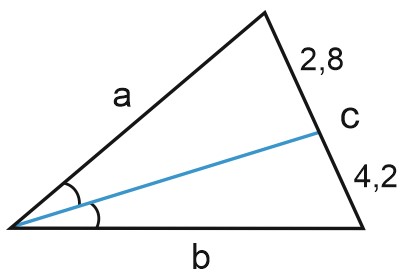
7. Биссектриса треугольника делит противоположную сторону на отрезки \(2,8\) и \(4,2\). Периметр треугольника равен \(22\). Найдите стороны треугольника.
Решение:
Пусть стороны треугольника равны \(a, \; b\) и \(c\). Биссектриса делит сторону \(c\) на отрезки \(2,8\) и \(4,2\).
Значит, \(c = 2,8 + 4,2 = 7.\)
В соответствии со свойством биссектрисы:
\(\displaystyle \frac{a}{b}=\frac{2,8}{4,2}=\frac{28}{42}=\frac{2}{3}.\)
Или: \(\displaystyle a=\frac{2}{3}b.\)
Одновременно выполнено условие для периметра: \(a+b+c = 22, \; a+b= 15.\)
Тогда \(\displaystyle \frac{5}{3}b=15, \; b=9, \; a=6.\)
Ответ: 9, 6, 7.