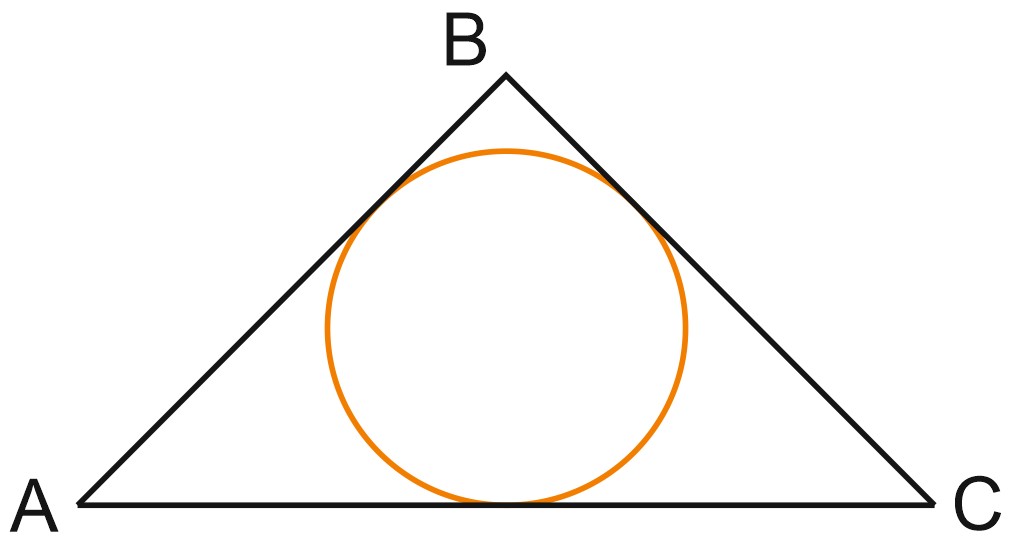
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
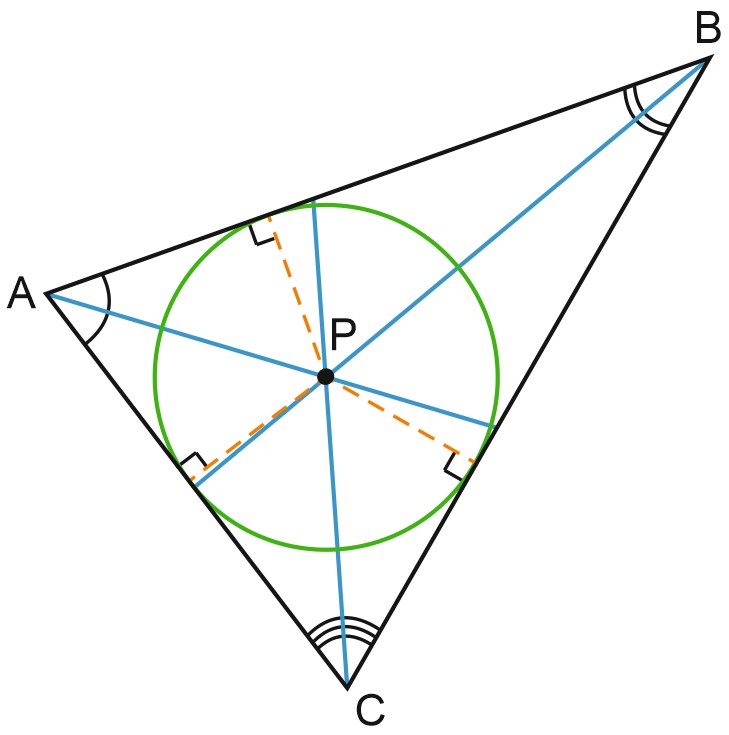
Ее центром является точка пересечения биссектрис треугольника.
Мы помним, что биссектриса угла – это множество точек, равноудаленных от сторон угла.
Пусть биссектрисы углов \(A\) и \(B\) треугольника пересекаются в точке \(P\).
Тогда точка \(P\) равноудалена от сторон \(AB\) и \(AC\), поскольку лежит на биссектрисе угла \(A\), а также от сторон \(BC\) и \(BA\), поскольку лежит на биссектрисе угла \(B\). Это значит, что точка \(P\) равноудалена от прямых \(AC\) и \(BC\), то есть лежит на биссектрисе угла \(C\).
Теорема доказана.
Радиус окружности \(r\), вписанной в прямоугольный треугольник с катетами \(a\) и \(b\) и гипотенузой \(c\), вычисляется по формуле: \(\displaystyle \frac{1}{2}(a+b-c)\).
Доказательство здесь: «Окружность вписана в прямоугольный треугольник».
1. Найдите диаметр окружности, вписанной в треугольник со сторонами \(13\), \(14\) и \(15\).
Решение:
Выразим площадь треугольника двумя разными способами:
\(\displaystyle S=pr,\)
\(\displaystyle S=\sqrt{p(p-a)(p-b)(p-c)},\) где \(\displaystyle p=\frac{a+b+c}{2}\) – полупериметр треугольника, \(a, \; b, \; c\) – его стороны.
\(\displaystyle p=\frac{13+14+15}{2}=21,\)
\(\displaystyle S=\sqrt{21(21-13)(21-14)(21-15)}=\sqrt{21\cdot 8\cdot 7\cdot 6}=84.\)
Тогда \(\displaystyle r=\frac{S}{p}=\frac{84}{21}=4\), а диаметр окружности равен \(8.\)
Ответ: 8.
2. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен \(2\). Найдите гипотенузу c этого треугольника. В ответе укажите \(c\left( \sqrt{2}-1 \right)\).
Решение:
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен \(a\). Тогда гипотенуза равна \(a\sqrt{2}\).
Запишем площадь треугольника \(ABC\) двумя способами:
\(S=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2} a^2.\)
\(S=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2}\left( 2a + a\sqrt{2}\right)r.\)
Приравняв эти выражения, получим, что \(a=\left( 2 + \sqrt{2}\right)r\). Поскольку \(r=2\), получаем, что \(a=4+2\sqrt{2}.\)
Тогда \(c=a\sqrt{2}=4+4\sqrt{2}=4\left( 1+\sqrt{2} \right).\)
В ответ запишем \(c\left( \sqrt{2}-1 \right)=4.\)
Ответ: 4.
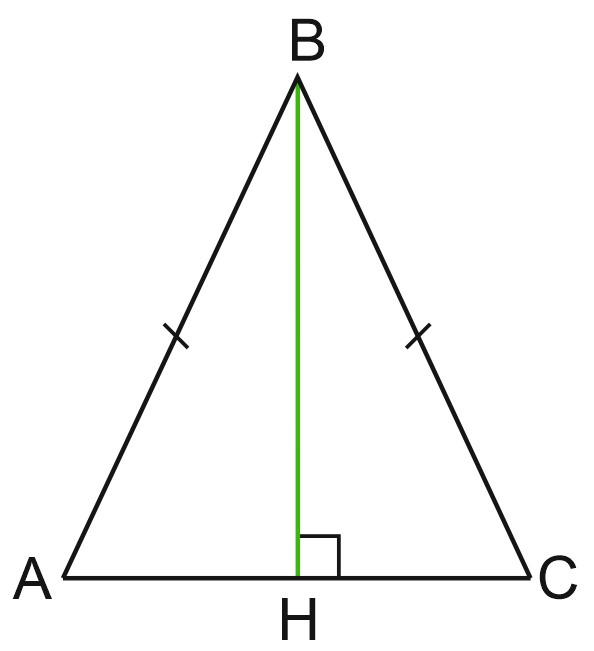
3. В равнобедренном треугольнике \(ABC\) основание \(AC\) равно \(10\) см, а высота, проведенная к основанию, \(12\) см. Найдите периметр треугольника и радиус вписанной окружности.
Решение:
Высота \(BH\), проведенная к основанию \(AC\), является медианой. Значит, \(AH = HC = 5\).
\(AB\) находится по теореме Пифагора из треугольника \(ABH\):
\(\displaystyle AB=\sqrt{AH^{2}+BH^{2}}=\sqrt{5^{2}+12^{2}}=13.\)
Периметр треугольника \(ABC\) – это сумма длин сторон, т. е. \(P = 13 + 13 + 10 = 36.\)
Площадь треугольника \(\displaystyle S=\frac{1}{2}AC\cdot BH=\frac{1}{2}\cdot 10\cdot 12=60.\)
Радиус вписанной окружности r найдем по формуле \(S = p r\):
\(\displaystyle r=\frac{S}{p}=\frac{60}{18}=\frac{10}{3}.\)
Ответ: \(\displaystyle 30; \frac{10}{3}.\)
4. Найдите площадь прямоугольного треугольника, если радиус описанной окружности равен \(5\), а вписанной \(1\).
Решение:
Пусть длина радиуса описанной окружности \(R = 5\), а длина радиуса вписанной окружности \(r = 1.\)
Мы знаем, что \(\displaystyle r=\frac{a+b-c}{2}, \; R=\frac{c}{2}, \; S=p\cdot r\), где \(\displaystyle p=\frac{a+b+c}{2}\) – полупериметр, \(a, \; b, \; c\) – стороны треугольника.
Значит, \(\displaystyle r=\frac{a+b-c}{2}=\frac{a+b+c-2c}{2}=\frac{a+b+c}{2}-\frac{2c}{2}=p-c=p-2R.\)
Отсюда \(\displaystyle r=p-2R, \; p=r+2R.\)
Тогда \(\displaystyle S=(r+2R)\cdot r=(1+2\cdot 5)\cdot 1=11.\)
Ответ: 11.
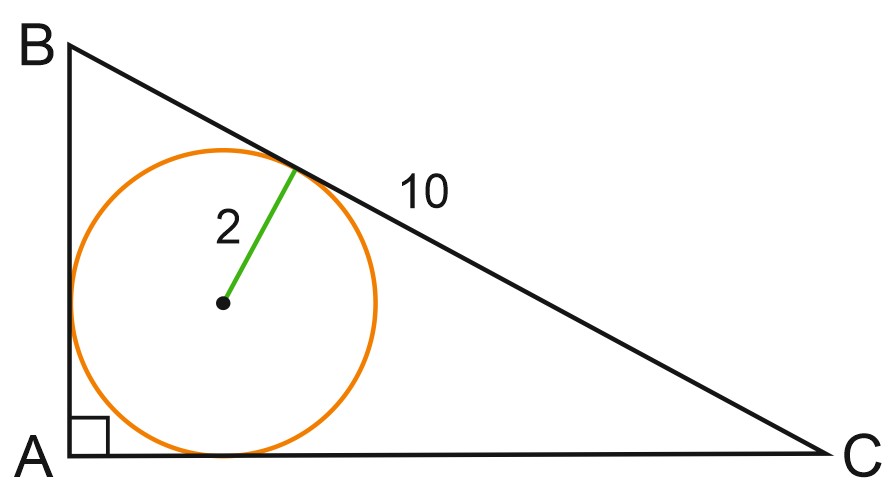
5. Найдите площадь прямоугольного треугольника, если радиус вписанной окружности равен \(2\), а гипотенуза \(10\).
Решение:
Пусть радиус вписанной окружности \(r = 2\), а гипотенуза \(c = 10.\)
Мы знаем, что в прямоугольном треугольнике \(\displaystyle r=\frac{a+b-c}{2}.\)
Значит, \(\displaystyle r=\frac{a+b-c}{2}=\frac{a+b+c-2c}{2}=\frac{a+b+c}{2}-\frac{2c}{2}=p-c, \; \) отсюда \(p =r+c.\)
Площадь находится по формуле \(S =pr, \; \) где \(\displaystyle p=\frac{a+b+c}{2}\) – полупериметр, \(a, \; b, \; c\) – стороны треугольника.
\(\displaystyle S=(r+c)\cdot r=(2+10)\cdot 2=24.\)
Ответ: 24.
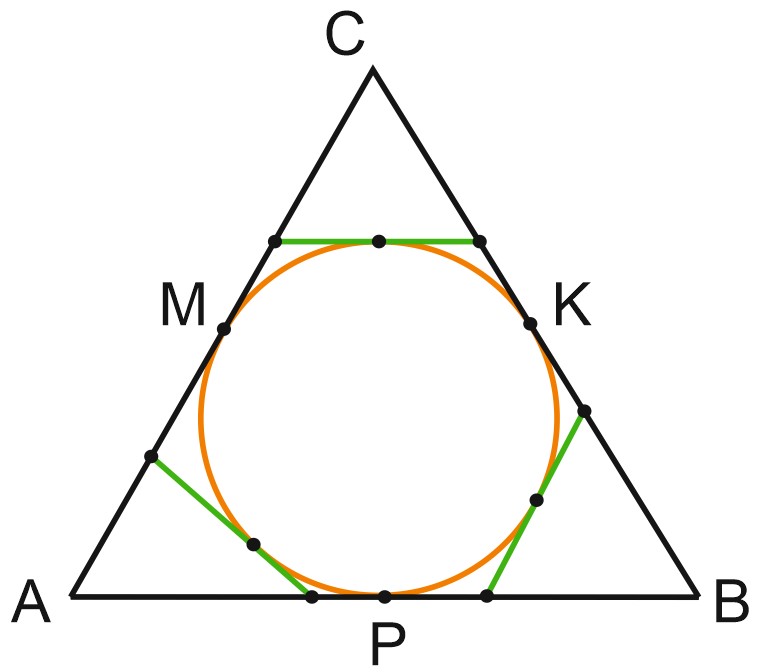
Если \(M\) – точка касания со стороной \(AC\) окружности, вписанной в треугольник \(ABC\), то \(AM = p – BC\), где \(p\) – полупериметр треугольника \(ABC\).
Доказательство:
Пусть \(M, \; K, \; P\) – точки касания вписанной окружности со сторонами \(AC, \; BC\) и \(AB\) соответственно.
Периметр треугольника \(ABC\) равен \(AB + BC + AC = AM + AP + CM + CK + BK + BP = 2 (AM + CK + BK)\), так как отрезки касательных, проведенных к окружности из одной точки, равны.
Но это значит, что периметр треугольника \(ABC\) равен \(2 (AM + BC).\)
Отсюда \(AM = p – BC, \; \) где \(p\) – полупериметр треугольника \(ABC\).
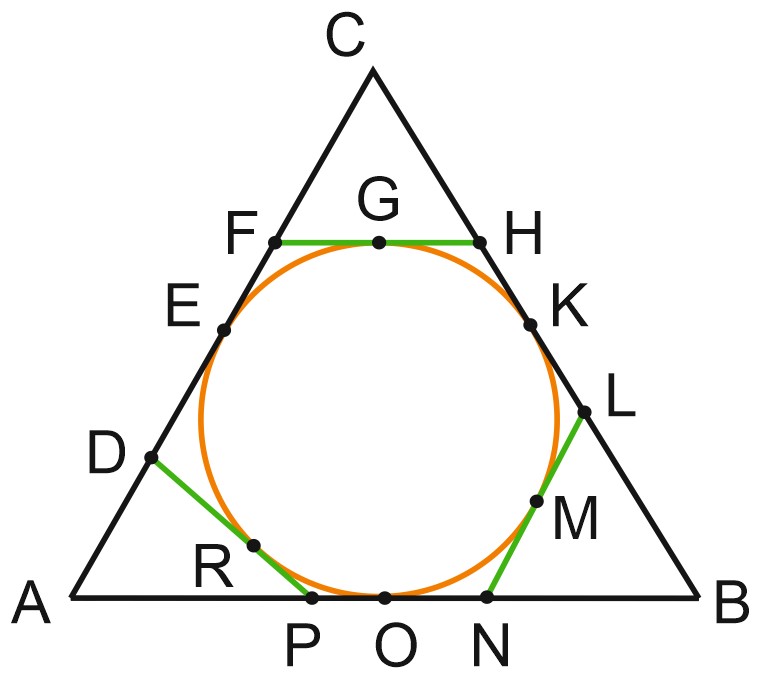
6. К окружности, вписанной в треугольник \(ABC\), проведены три касательные. Периметры отсеченных треугольников равны \(8, \; 12, \; 18\). Найдите периметр данного треугольника.
Решение:
Периметр треугольника \(ABC\) равен \(AD + DE + EF + FC + CH + HK + KL + LB + BN + NO + OP + PA.\)
Отрезки касательных, проведенных из одной точки к окружности, равны.
\(DE = DR, \; EF = FG, \; HK = HG, \; KL = LM…\)
Мы получили, что периметр треугольника \(ABC\) равен сумме периметров отсеченных от окружности треугольников, то есть \(8+12+18=38.\)
Ответ: 38.
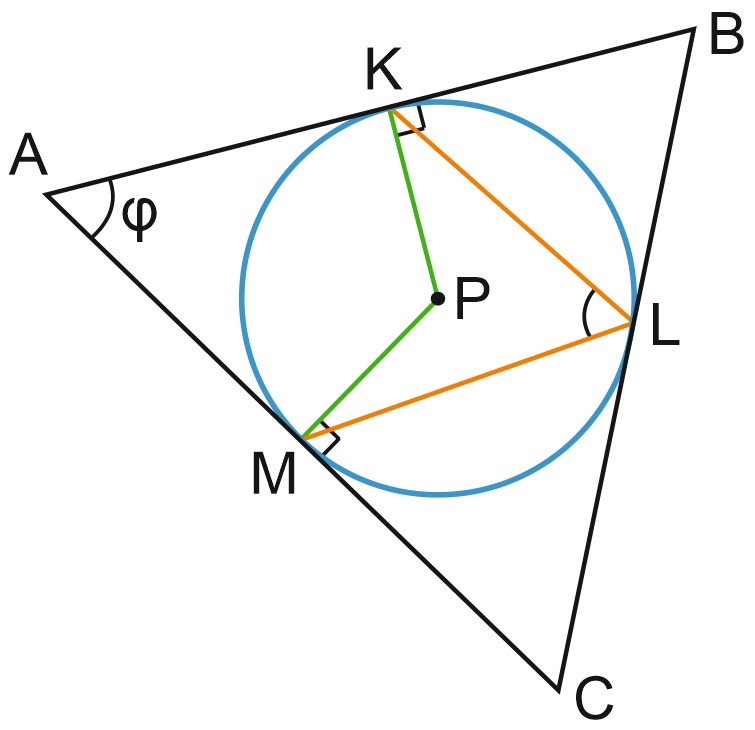
Если окружность, вписанная в треугольник \(ABC\), касается сторон \(AB, \; BC\) и \(AC\) соответственно в точках \(K, \; L, \; M,\) а угол \(BAC\) равен \(\varphi\), то угол \(KLM\) равен \(90 ^{\circ} - \displaystyle \frac{1}{2}\varphi.\)
Доказательство:
Пусть \(P\) – центр вписанной окружности треугольника \(ABC\).
В четырехугольнике \(AMPK\) углы \(K\) и \(M\) – прямые (как углы между касательной и радиусом).
Сумма углов четырехугольника \(AMPK\) равна \(360\) градусов.
Значит, \(\angle KPM = 180 ^{\circ} - \angle MAK.\)
Угол \(KLM\) – вписанный, и его величина равна половине угла \(KPM\), то есть \(90 ^{\circ} -\displaystyle \frac{1}{2}\varphi.\).
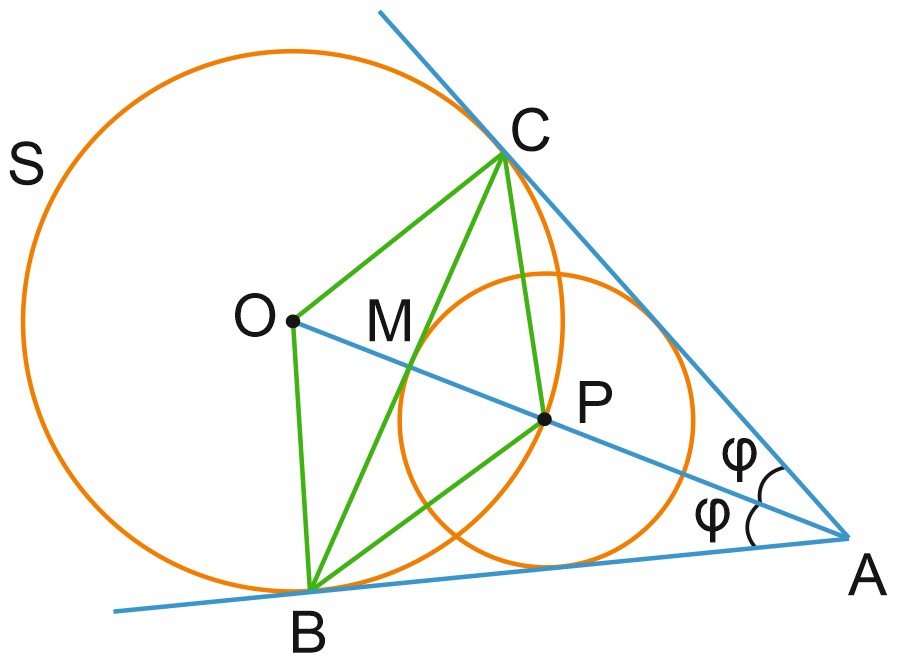
Если прямые, проходящие через точку \(A\), касаются окружности \(S\) в точках \(B\) и \(C\), то центр вписанной окружности треугольника \(ABC\) лежит на окружности \(S\).
Доказательство:
Пусть \(O\) – центр окружности \(S, \; P\) – точка пересечения окружности \(S\) и отрезка \(AO\). Центр окружности, вписанной в угол, лежит на биссектрисе угла. Значит, \(AO\) – биссектриса угла \(BAC\).
Пусть угол \(OAB\) равен \(\varphi\). Тогда угол \(AOC\) равен \(90^{\circ}-\varphi\), а угол \(CBP\) равен \(\displaystyle \frac{1}{2}\left ( 90^{\circ}-\varphi \right ) \) – как вписанный угол, опирающийся на дугу \(CP\), – то есть половине угла \(ABM\). Это значит, что \(BP\) – биссектриса угла \(ABC\) и \(P\) – точка пересечения биссектрис треугольника \(ABC\) и центр окружности, вписанной в треугольник \(ABC\).