Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.
Докажем что биссектриса угла – это множество точек, равноудаленных от его сторон. Это значит, что от любой точки, лежащей на биссектрисе угла, расстояния до сторон угла равны.
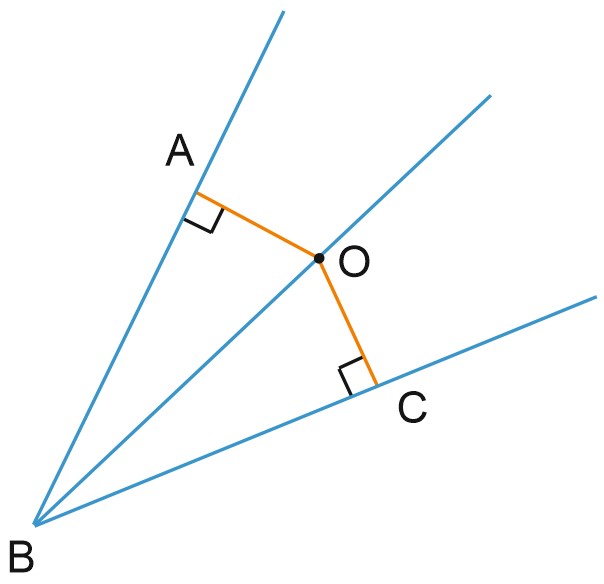
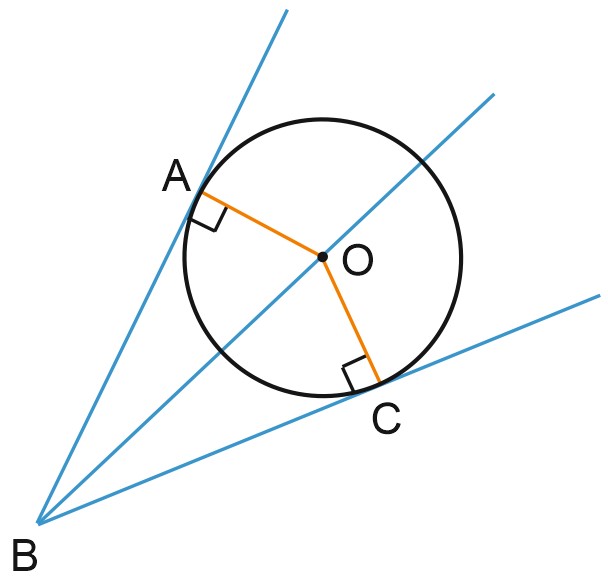
Пусть точка \(O\) лежит на биссектрисе угла \(ABC\). Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую, поэтому треугольники \(BOC\) и \(BOA\) на рисунке – прямоугольные.
Здесь отрезки \(OA\) и \(OC\) – расстояния от точки \(O\) до сторон \(BA\) и \(BC\) угла \(ABC\).
Прямоугольные треугольники \(BOC\) и \(BOA\) равны по острому углу и гипотенузе. Значит, \(OA=OC\) и любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.
Построение биссектрисы угла
Решим с помощью циркуля и линейки задачу на построение: поделим угол пополам. И давайте подумаем: с чего мы начинаем задачи на построение?
Как и в жизни, сначала мы формулируем цель. Что мы хотим построить, какими свойствами обладает этот объект?
Хотим поделить угол пополам, значит, нам нужна биссектриса угла. Предположим, что биссектриса угла уже построена. Какие же у нее свойства?
Нарисуем угол \(ABC\) и проведем его биссектрису \(BO\). Как мы доказали, любая точка, лежащая на биссектрисе угла, равноудалена от сторон этого угла.
Теперь понятно, как строить биссектрису угла.
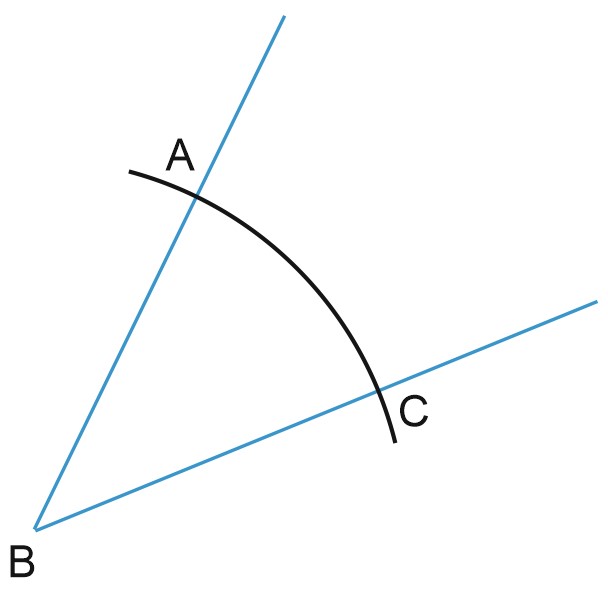
Построим окружность с центром в точке \(B\) и производным радиусом. Она пересекает стороны угла в точках \(A\) и \(C\).
Найдем середину отрезка \(AC\) с помощью циркуля и линейки. Мы уже умеем это делать.
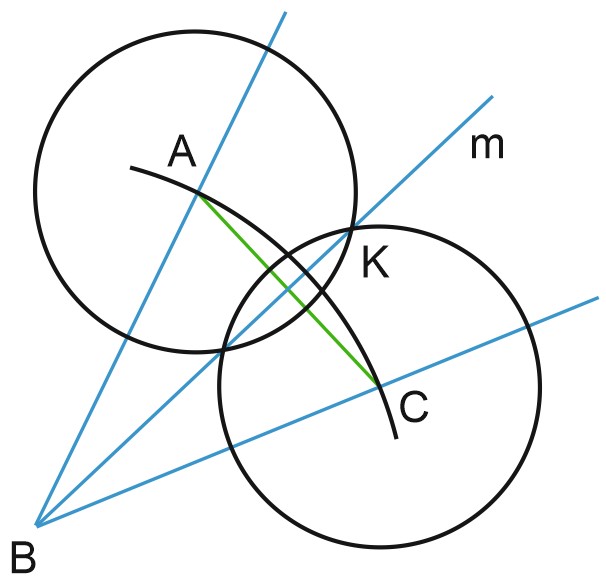
Для этого построим две окружности с центрами в точках \(A\) и \(C\) и радиусом большим, чем половина \(AC\). Через точки пересечения этих окружностей проведем прямую, которая пересекает отрезок \(AC\) в точке \(K\). О чудо! Вершина угла \(B\) тоже лежит на этой прямой!
Докажем, что луч \(BK\) – это биссектриса угла \(B\). По построению, треугольник \(ABC\) – равнобедренный, \(AB=BC\). Точка \(K\) – середина \(AC\). Тогда \(BK\) – медиана, а также высота и биссектриса равнобедренного треугольника \(ABC.\)
Таким образом, мы можем построить биссектрису любого угла.
Мы видим, что задачи на построение состоят из нескольких шагов:
\(1)\) Анализ. Предположим, что мы уже построили то, что нам нужно. Какими свойствами обладает этот объект?
\(2)\) Построение.
\(3)\) Доказательство. Мы доказываем, что построили именно то, что хотели.
\(4)\) Исследование. Всегда ли можно выполнить такое построение? Единственное ли решение у задачи?
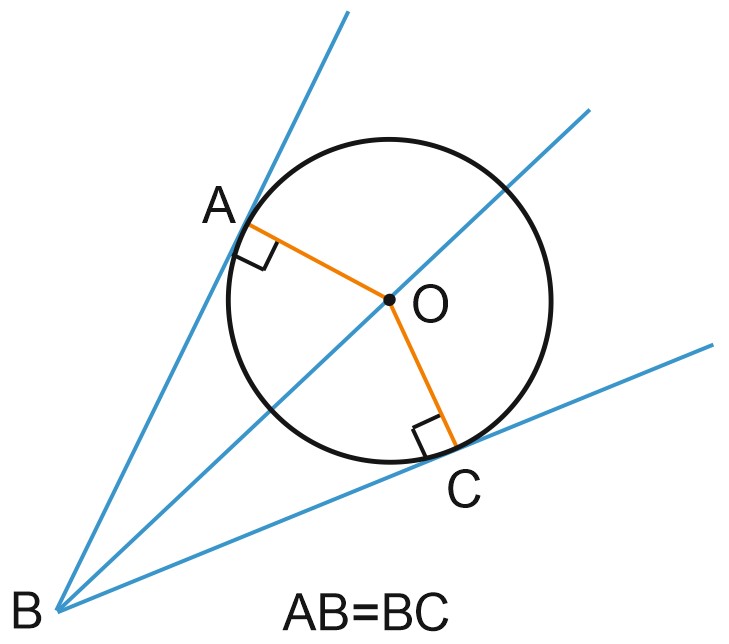
Нарисуем окружность с центром в точке \(O\), лежащей на биссектрисе угла \(ABC\), и радиусом \(OA\). Эта окружность пройдет также через точку \(C\), поскольку \(OA=OC\). Такая окружность касается сторон угла и называется вписанной в угол.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Можно посмотреть на нашу картину по-другому. Сказать, что к окружности с центром \(O\) проведены две касательные из точки \(B\), то есть две прямые, проходящие через точку \(B\) и касающиеся окружности в точках \(A\) и \(C\).
Напомним, что касательная к окружности – это прямая, имеющая с окружностью единственную общую точку.
Прямоугольные треугольники \(AOB\) и \(COB\) равны по острым углам и гипотенузе, \(AB=BC\). Мы доказали важную теорему:
Отрезки касательных, проведенные к окружности из одной точки, равны.
Рисунок с окружностью, вписанной в угол, легко запомнить.
Помните забавное «определение» биссектрисы? Биссектриса – это крыса, которая бегает по углам и делит угол пополам.
Нарисуем угол, который крыса делит пополам, и эта крыса тащит за собой (на хвосте) круглый сыр. Центр окружности, вписанной в угол, лежит на биссектрисе угла.
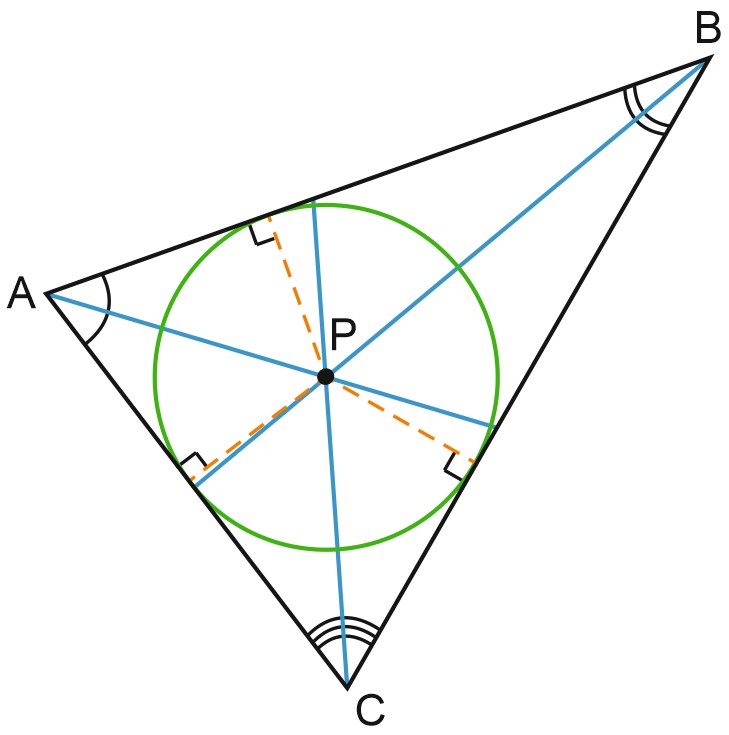
А если провести три биссектрисы в треугольнике? Точка их пересечения одинаково удалена от всех сторон треугольника.
Эта точка является центром окружности, вписанной в треугольник.
Биссектрисы смежных углов перпендикулярны.
Доказательство:
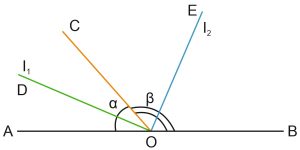
\(α\) и \(β\) – смежные углы, \(l_1\) – биссектриса угла \(α\), \(l_2\) – биссектриса угла \(β\). Докажем, что \(l_1 \perp l_2\).
Смежные углы – это углы, имеющие общую сторону, и их сумма равна \(180°\). Так как углы \(α\) и \(β\) – смежные, \(∠AOC+∠COB=180°.\)
\(∠DOC=1/2 α,\)
\(∠COE=1/2 β,\)
\(∠DOC+∠COE=\displaystyle \frac{1}{2} (α+β)=\frac{1}{2}\cdot180°=90°,\)
\(∠DOE=90°.\) Значит, \(l_1 \perp l_2\), что и требовалось доказать.