Треугольник вписан в окружность
Вписанный треугольник – треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Иногда говорят, что окружность описана около треугольника. Это означает то же самое – все вершины треугольника лежат на окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Ее центр – это точка пересечения серединных перпендикуляров к сторонам треугольника.
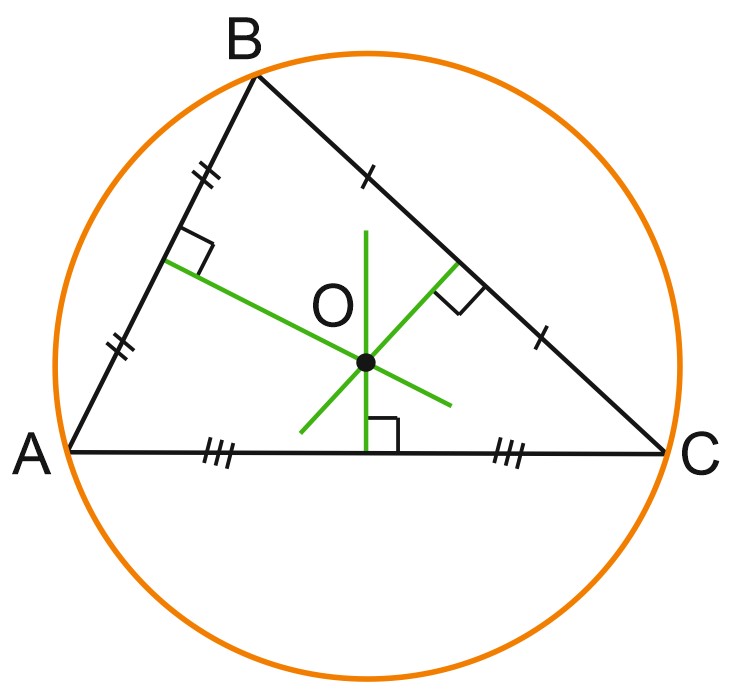
Доказательство:
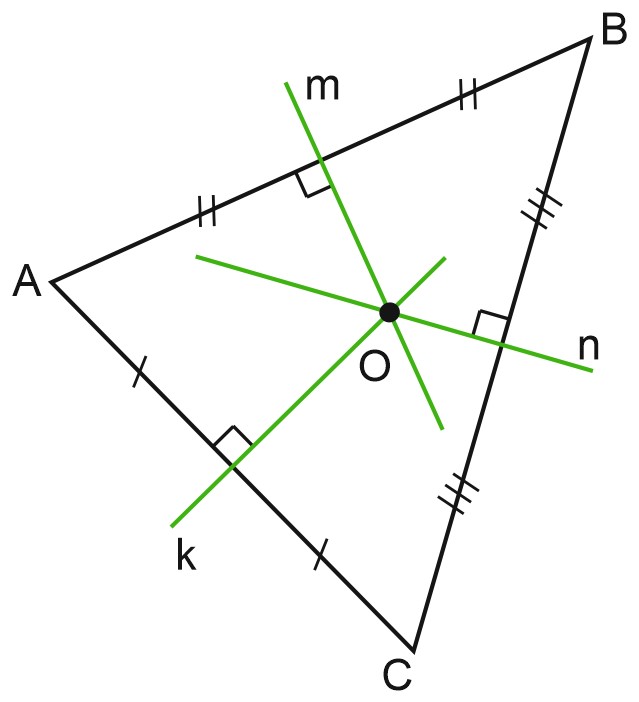
Пусть \(m\) – серединный перпендикуляр к стороне \(AB\), \(n\) – серединный перпендикуляр к стороне \(BC\), прямые \(m\) и \(n\) пересекаются в точке \(O\).
Серединный перпендикуляр к отрезку – это множество точек, равноудаленных от его концов.
Точка \(O\) равноудалена от точек \(A\) и \(B\) (поскольку \(O\in m\)), а также от точек \(B\) и \(C\), поскольку \(O\in n\).
Получаем, что точка \(O\) равноудалена также от точек \(A\) и \(C\), то есть \(O\in k\) – серединному перпендикуляру к \(AC\).
Это значит, что три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке. Точка \(O\) равноудалена от \(A\), \(B\) и \(C\) и потому является центром окружности, описанной вокруг треугольника \(ABC\).
Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы, а радиус этой окружности равен половине гипотенузы.
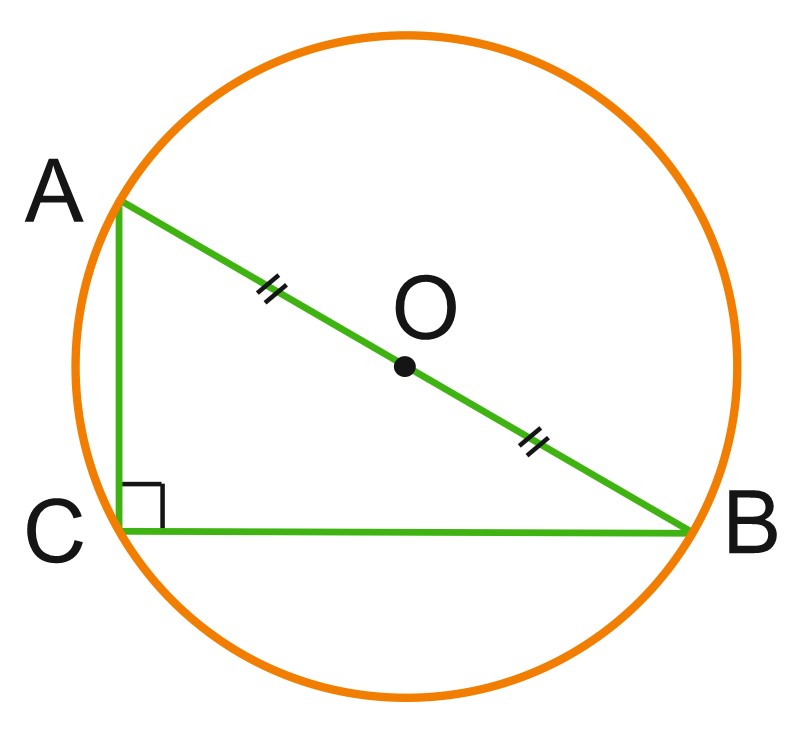
Доказательство:
Медиана, проведенная к гипотенузе, равна ее половине, по свойству медианы прямоугольного треугольника.
Его доказательство можно найти здесь: Медиана прямоугольного треугольника.
Поэтому середина гипотенузы – это точка, равноудаленная от вершины прямого угла и от концов гипотенузы, то есть от всех вершин прямоугольного треугольника.
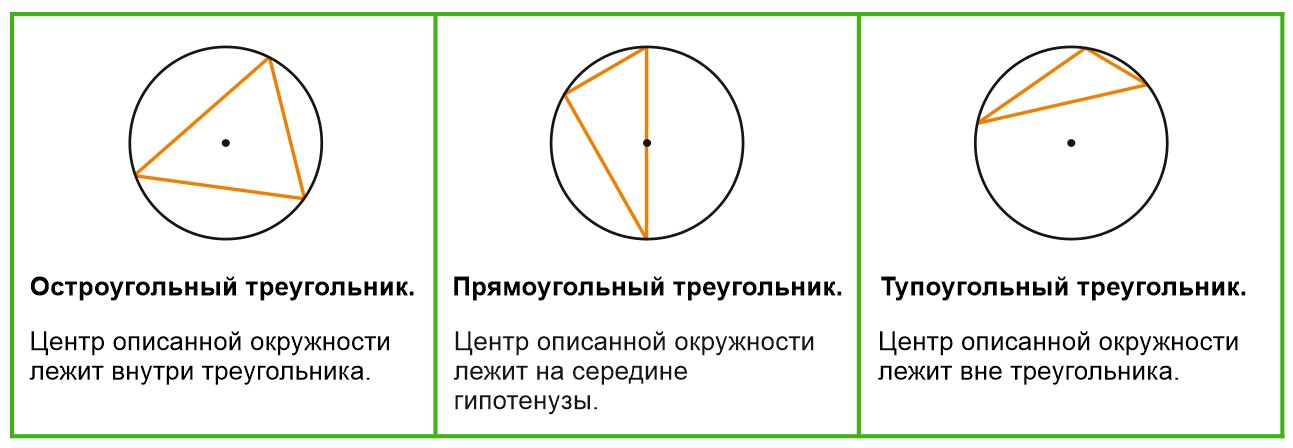
Центр окружности, описанной вокруг остроугольного треугольника, лежит внутри этого треугольника.
Центр окружности, описанной вокруг тупоугольного треугольника, лежит вне этого треугольника.
Теорема синусов:
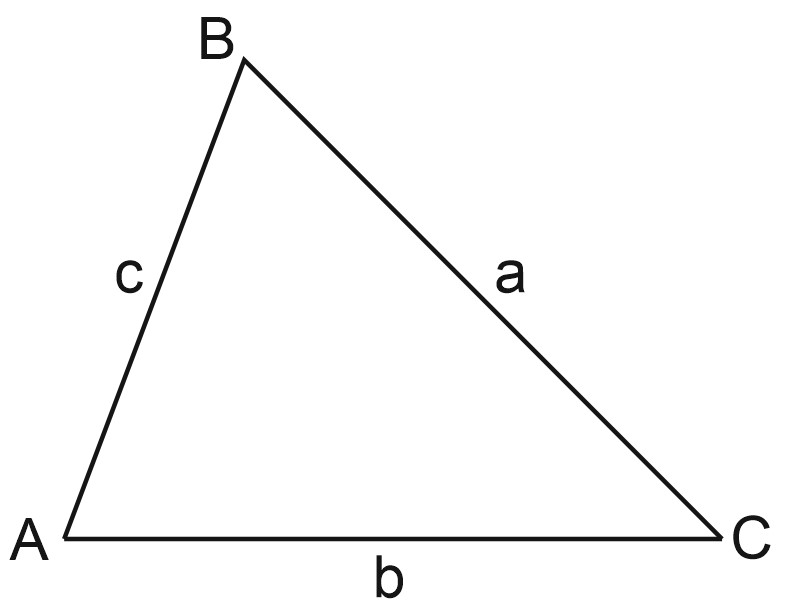
\(\displaystyle\frac{a}{sin\angle A}=\frac{b}{sin\angle B}=\frac{c}{sin\angle C}=2R,\)
R — радиус описанной окружности.
1. В треугольнике \(ABC\) сторона \(AB\) равна \(7\sqrt{3}\), а угол \(B\) равен \(120^{\circ}\). Найдите радиус описанной около этого треугольника окружности.

Решение:
По теореме синусов \(\displaystyle \frac{AC}{sin B}=2R.\)
Тогда \(\displaystyle R=\frac{7\sqrt{3}}{2}:\frac{\sqrt{3}}{2}=7.\)
Ответ: 7.
2. В треугольнике \(ABC\) угол \(A\) равен \(57^{\circ}\), а угол \(B\) – \(93^{\circ}\). Найдите радиус окружности, описанной около треугольника \(ABC\), если сторона \(AB\) равна \(10\).

Решение:
Зная, что сумма углов треугольника равна \(180^{\circ}\), найдем угол \(C\).
\(\displaystyle \angle C = 180^{\circ }-(\angle A+\angle B)=180^{\circ }-(53^{\circ }+97^{\circ })=30^{\circ }.\)
По теореме синусов \(\displaystyle \frac{AB}{sinC}=\frac{BC}{sinA}=\frac{AC}{sinB}=2R.\)
Значит, \(\displaystyle R=\frac{AB}{2sinC}=10.\)
Ответ: 10.
3. Сторона \(AC\) треугольника\(ABC\) с тупым углом \(B\) равна радиусу описанной около него окружности. Найдите угол \(B\). Ответ дайте в градусах.
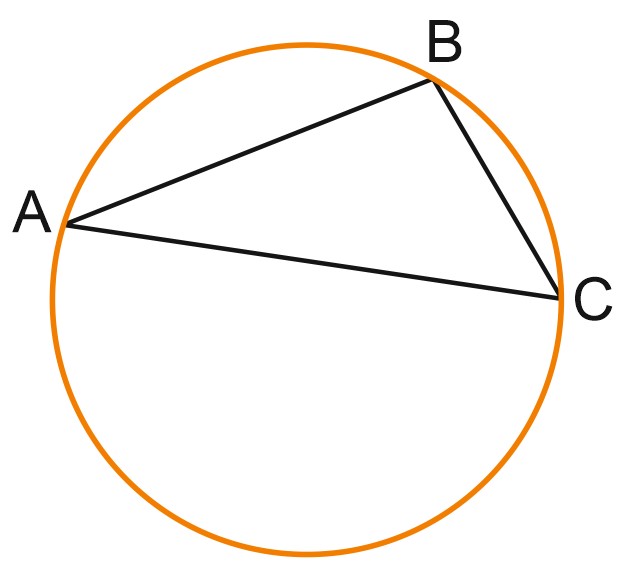
Решение:
По теореме синусов, \(\genfrac{}{}{}{0}{AC}{\sin B}=2R.\)
Получаем, что \(\sin B=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2}\). Угол \(B\) — тупой. Значит, он равен \(150^{\circ}\).
Ответ: 150.
4. Боковые стороны равнобедренного треугольника равны \(40\), основание равно \(48\). Найдите радиус описанной окружности этого треугольника.
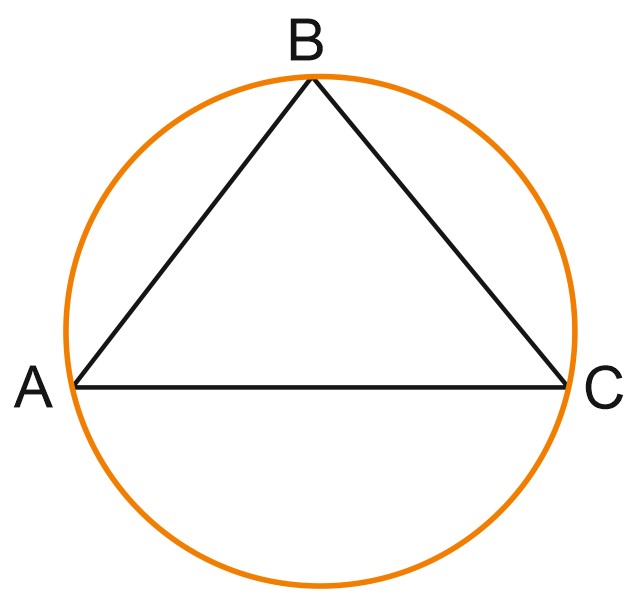
Решение:
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
\(S=\genfrac{}{}{}{0}{abc}{4R}.\)
\(S=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2} ah\), где \(h\) — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону \(AB\) пополам. По теореме Пифагора найдем \(h=32\).
Тогда \(R=25\).
Ответ: 25.
5. В равнобедренном треугольнике \(ABC\) основание \(AC\) равно \(10\) см, а высота, проведенная к основанию, \(12\) см. Найдите периметр треугольника и радиус вписанной окружности.

Решение:
Высота \(BH\), проведенная к основанию \(AC\), является медианой. Значит, \(AH = HC = 5\).
\(AB\) находится по теореме Пифагора из треугольника \(ABH\):
\(\displaystyle AB=\sqrt{AH^{2}+BH^{2}}=\sqrt{5^{2}+12^{2}}=13.\)
Периметр треугольника \(ABC\) – это сумма длин сторон, т. е. \(P = 13 + 13 + 10 = 36.\)
Площадь треугольника \(\displaystyle S=\frac{1}{2}AC\cdot BH=\frac{1}{2}\cdot 10\cdot 12=60.\)
Радиус вписанной окружности \(r\) найдем по формуле \(S = p r\):
\(\displaystyle r=\frac{S}{p}=\frac{60}{18}=\frac{10}{3}.\)
Ответ: \(\displaystyle 30; \frac{10}{3}.\)
6. Стороны \(AB\) и \(BC\) треугольника \(ABC\) равны \(6\) и \(3\sqrt{2}\) соответственно, угол \(B- 45^{\circ }\). Найдите диаметр окружности, описанной около треугольника \(ABC\).

Решение:
Найдем длину стороны \(AC\) по теореме косинусов, используя длины сторон \(AB\), \(CB\) и косинус угла \(B\), противолежащего стороне \(AC\):
\(\displaystyle AC^{2}=AB^{2}+BC^{2}-2\cdot AB\cdot BC\cdot cosB=6^{2}+(3\sqrt{2})^{2}-2\cdot 6\cdot 3\sqrt{2}\cdot \frac{\sqrt{2}}{2}=18,\)
\(AC=3\sqrt{2}.\)
Теперь воспользуемся теоремой синусов:
\(\displaystyle \frac{AC}{sin45^{\circ }}=2R,\)
\(\displaystyle 2R=3\sqrt{2}:\frac{\sqrt{2}}{2}=6.\)
Значит, диаметр окружности, описанной около треугольника \(ABC\), равен \(6\).
Ответ: 6.
7. Найдите площадь прямоугольного треугольника, если радиус описанной окружности равен \(5\), а вписанной \(1\).
Решение:
Пусть длина радиуса описанной окружности \(R = 5\), а длина радиуса вписанной окружности \(r = 1.\)
Мы знаем, что \(\displaystyle r=\frac{a+b-c}{2}, \; R=\frac{c}{2}, \; S=p\cdot r\), где \(\displaystyle p=\frac{a+b+c}{2}\) – полупериметр, \(a, \; b, \; c\) – стороны треугольника.
Значит, \(\displaystyle r=\frac{a+b-c}{2}=\frac{a+b+c-2c}{2}=\frac{a+b+c}{2}-\frac{2c}{2}=p-c=p-2R.\)
Отсюда \(\displaystyle r=p-2R, \; p=r+2R.\)
Тогда \(\displaystyle S=(r+2R)\cdot r=(1+2\cdot 5)\cdot 1=11.\)
Ответ: 11.
Если вам понравился наш материал - записывайтесь на курсы подготовки к ЕГЭ по математике онлайн.

























































