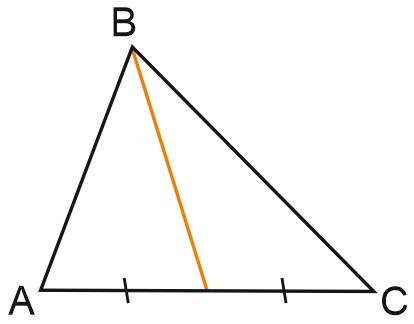
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
Докажем эту теорему.
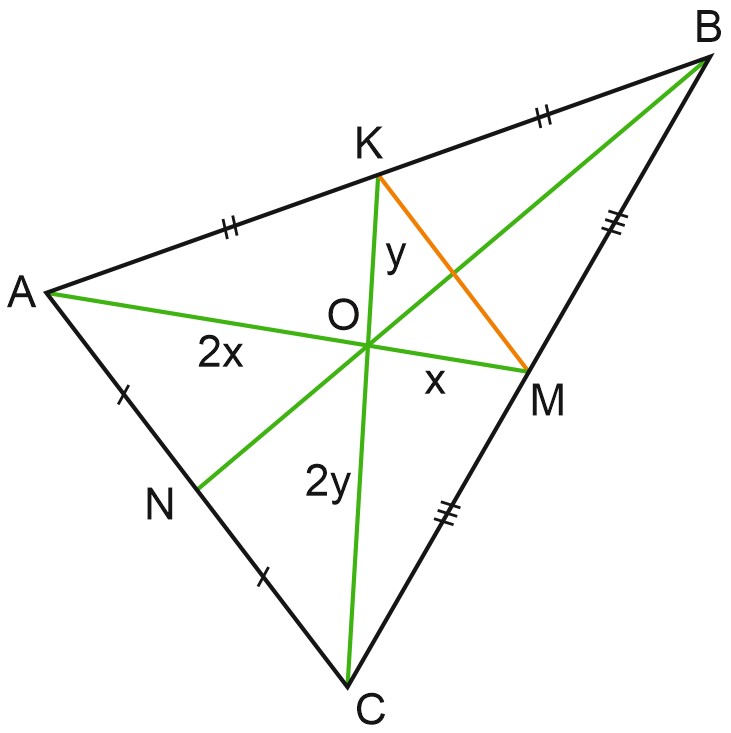
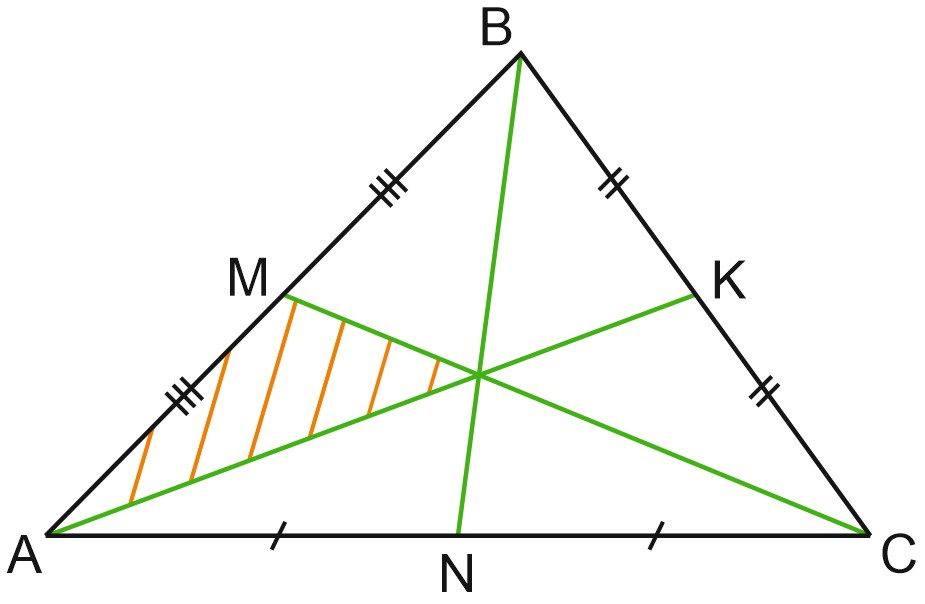
Проведем в треугольнике \(ABC\) медианы \(AM\) и \(CK\). Пусть \(AM\) и \(CK\) пересекаются в точке \(O\).
Тогда \(MK\) – средняя линия треугольника \(ABC\), и треугольник \(OMK\) подобен треугольнику \(OAC\) по двум углам.
\(\displaystyle MK=\frac{1}{2}AC, \; MK \parallel AC\). Запишем соотношение сходственных сторон треугольников \(OMK\) и \(OAC\).
\(\displaystyle \frac{OA}{OM}=\frac{OC}{OK}=\frac{AC}{MK}=\frac{2}{1}\).
Медианы \(AM\) и \(CK\) в точке пересечения делятся в отношении \(2:1\), считая от вершины.
Осталась третья медиана – \(BL\).
Предположим, что \(\displaystyle BL\cap AM=O_1\). Тогда в точке \(O_1\) медианы \(BL\) и \(AM\) делятся в отношении \(2 : 1\).
Но если \(\displaystyle \frac{O_1A}{O_1M}=\frac{OA}{OM}=\frac{2}{1}\), то точка \(O_1\) совпадает с точкой \(O\), и это значит, что три медианы треугольника пересекаются в точке \(O\) и делятся в ней в отношении \(2:1\), считая от вершины.
Теорема доказана.
Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.
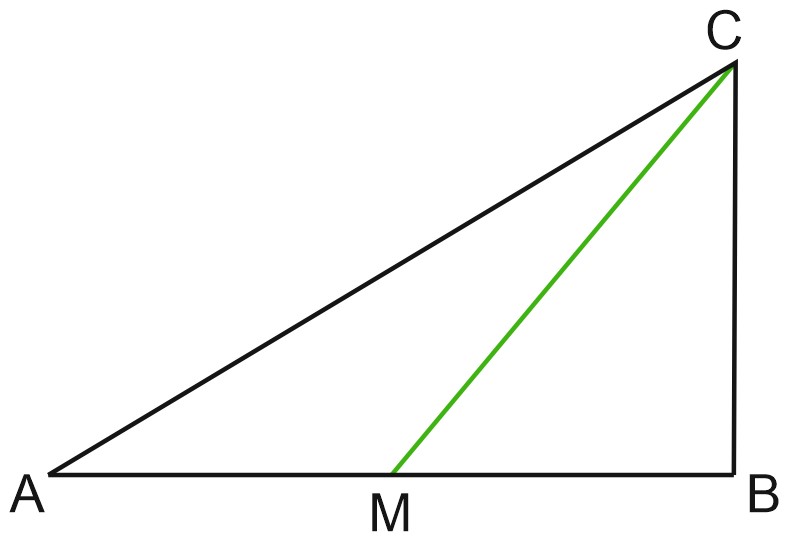
На рисунке \(CM\) – медиана треугольника \(ABC\). Площадь треугольников \(ACM\) и \(BCM\) равны. Действительно, у этих треугольников равные основания \(AM\) и \(BM\) и одна и та же высота.
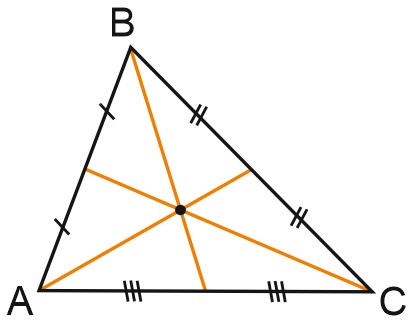
Три медианы треугольника делят его на шесть равных по площади треугольников.
На рисунке все 6 треугольников, из которых состоит треугольник \(ABC\), имеют равные площади.
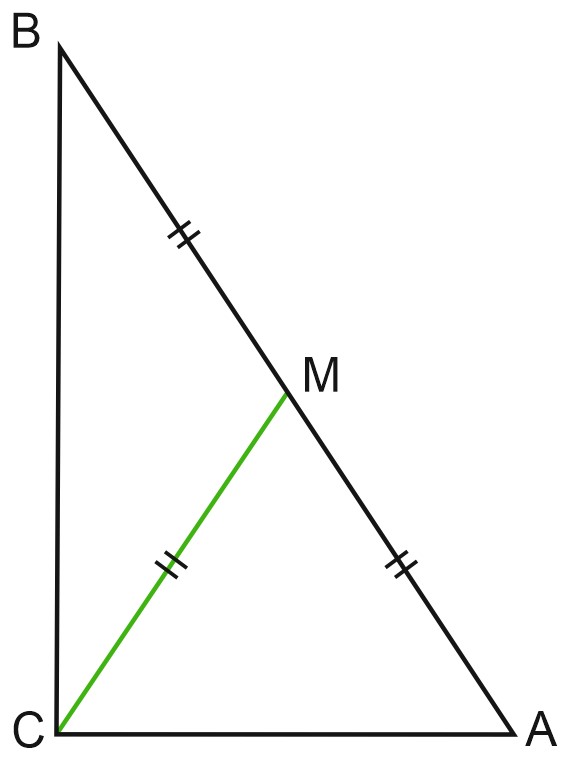
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
Задачи ЕГЭ по теме «Медианы треугольника»
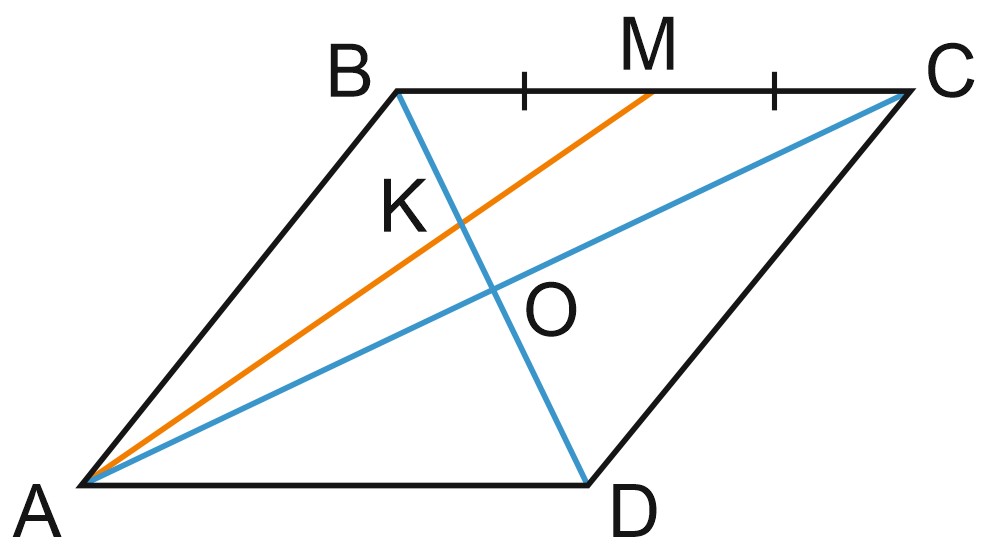
1. В параллелограмме \(ABCD\) отмечена точка \(M\) – середина стороны \(BC\). Отрезки \(BD\) и \(AM\) пересекаются в точке \(K\). Найдите\(BK\), если \(BD=18\).
Решение:
Пусть \(O\) – точка пересечения диагоналей параллелограмма.
Диагонали параллелограмма в точке пересечения делятся пополам, поэтому \(BO\) – медиана треугольника \(ABC\).
Тогда \(K\) – точка пересечения медиан треугольника \(ABC\).
Медианы треугольника в точке пересечения делятся в отношении \(2 : 1\), считая от вершины.
Поэтому \(BK=\displaystyle \frac{2}{3}BO=\frac{1}{3}BD=6\).
Вот еще полезный факт. Площадь треугольника, составленного из медиан данного треугольника, равна \(\displaystyle \frac{3}{4}S\), где \(S\) – площадь данного треугольника.
Читайте доказательство.