Анна Малкова
Об этой теореме можно сказать: в учебнике нет, а на экзамене есть. Конечно, в учебнике она тоже есть – но никак не выделена и найти ее почти невозможно.
Множество задач ЕГЭ и ОГЭ решаются с помощью этой теоремы.
Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.
\(MC^2=MA \cdot MB\).
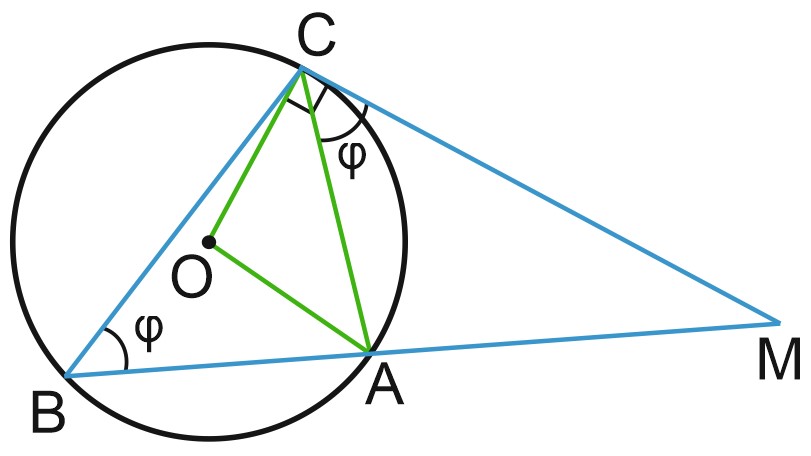
Пусть \(MC\) – касательная, \(MB\) - секущая к окружности. Покажем, что \(MC^2=MA \cdot MB\)
Как мы доказали \(\angle MCA = \angle ABC = \varphi\), и это значит, что треугольники \(MCA\) и \(MBC\) подобны по двум углам.
Запишем соотношение сходственных сторон: \(\displaystyle \frac{MC}{MB}=\frac{MA}{MC}\).
Отсюда \(MC^2=MA \cdot MB\).