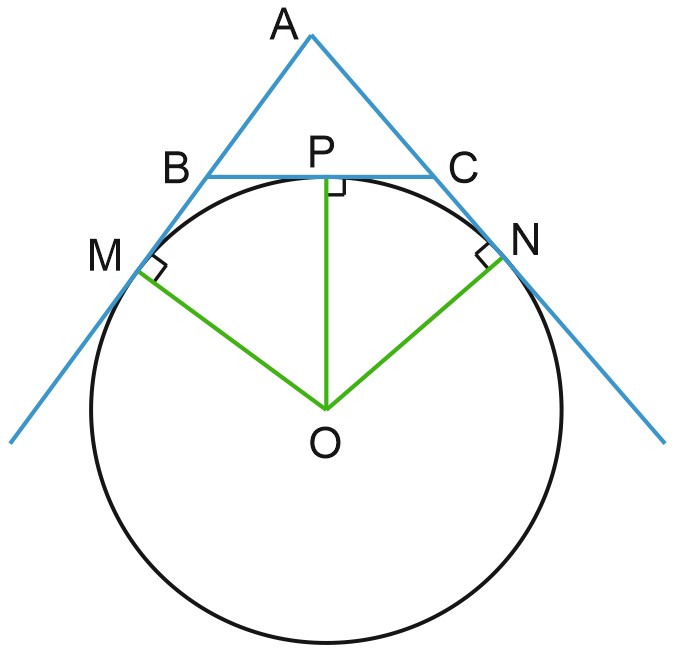
Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью треугольника.
Центр вписанной окружности – это точка пересечения биссектрисы угла треугольника и биссектрис внешних углов при двух других его вершинах.
Если окружность касается стороны \(BC\) треугольника \(ABC\) и продолжений сторон \(AB\) и \(AC\), то расстояние от вершины \(A\) до точки касания окружности с прямой \(AB\) равно полупериметру треугольника \(ABC\).
Пусть \(P\) – точка касания окружности со стороной \(BC\) треугольника \(ABC, \; M\) и \(N\) – точки касания с продолжениями сторон \(AB\) и \(AC\).
Докажем, что \(AN=\displaystyle \frac{1}{2}P_{ABC}.\)
Отрезки касательных, проведенных из одной точки, равны.
Значит, \(AN=AM;\)
\(AN=AC+CN=AC+CP;\)
\(AМ=AB+BM=AB+BP;\)
\(AN = AM,\)
\(2AN=AC+AB+CP+BP =AC+AB+BC;\)
\(AN=\displaystyle \frac{1}{2}P_{ABC}.\)
Подробнее о центре вневписанной окружности: «Лемма о трезубце».
Задача ЕГЭ, Профильный уровень
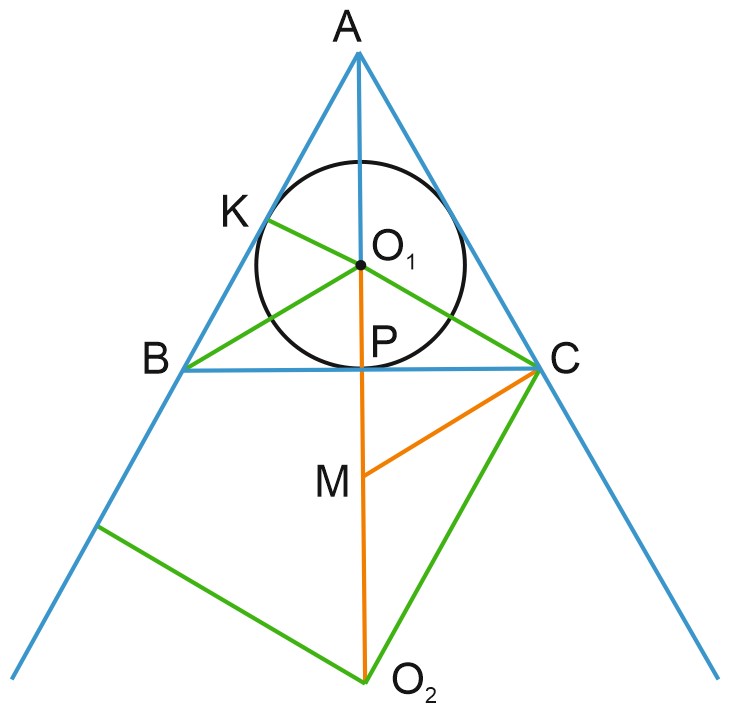
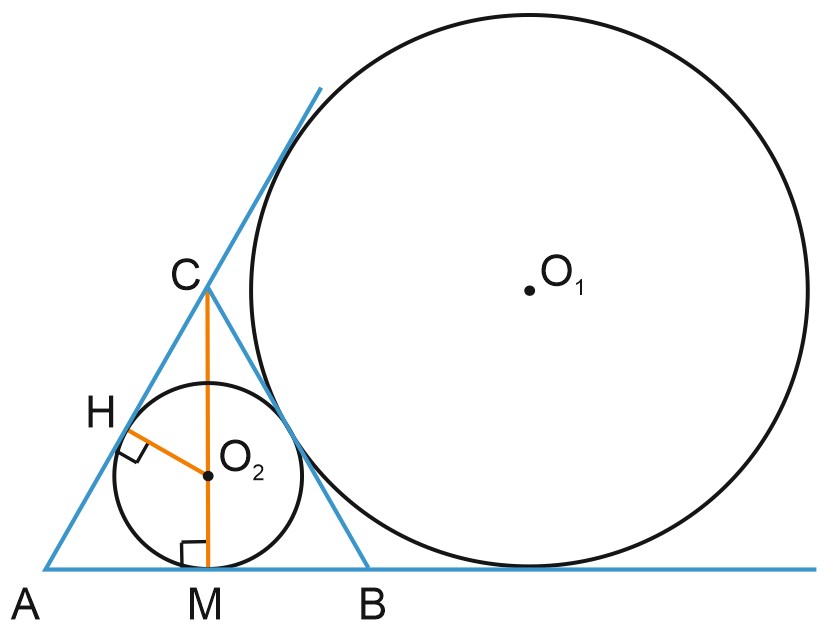
1. Прямые, содержащие катеты \(AC\) и \(CB\) прямоугольного треугольника \(ABC\), являются общими внутренними касательными к окружностям радиусов \(4\) и \(8\). Прямая, содержащая гипотенузу \(AB\), является их общей внешней касательной.
а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника \(ACB\).
б) Найдите площадь треугольника \(ACB\).
Решение:
Пусть \(L, \; K, \; M, \; N, \; P, \; Q\) – точки касания.
а) Докажем, что \(AN=\displaystyle \frac{1}{2}P_{ABC}.\)
Отрезки касательных, проведенных из одной точки, равны.
Значит, \(AN=AP;\)
\(AN=AC+CN=AC+CQ;\)
\(AP=AB+BP=AB+BQ;\)
\(2AN=AC+AB+CQ+BQ =AC+AB+BC;\)
\(AN=\displaystyle \frac{1}{2}P_{ABC}.\)
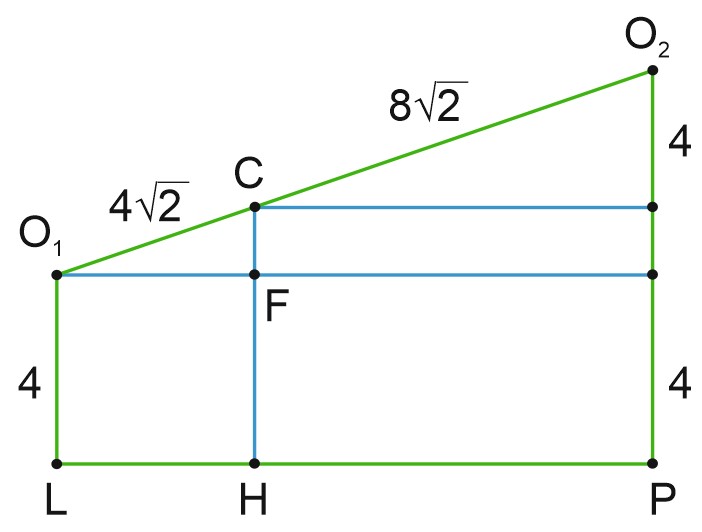
б) Найдем \(S_{\triangle ABC}\), если, \(r=O_1 M=4, \; R=O_2 N=8.\)
Поскольку \(CMO_1K\) и \(CNO_2Q\) – квадраты, \(MC=4, \; QC=8,\)
\(C\in O_1O_2, \; O_1C=4\sqrt{2}, \; O_2C=8\sqrt{2}.\)
Рассмотрим трапецию \(O_1O_2PL.\)
\({{\rm O}}_{{\rm 1}}{\rm L}{\rm =4,\ }{{\rm O}}_{{\rm 2}}{\rm P}{\rm =8,\ }{\rm O}{{\rm O}}_{{\rm 1}}{\rm =4}\sqrt{{\rm 2}}{\rm +8}\sqrt{{\rm 2}}{\rm =12}\sqrt{{\rm 2}}.\)
Точка \(C\) делит сторону \(O_1O_2\) в отношении \(O_1 C: O_2 C=1:2.\) Тогда \(CF=\displaystyle \frac{4}{3}.\)
Проведем \(CH\), причем \(CH\) – высота треугольника \(ABC\).
\(CH=CF+FH=\displaystyle \frac{4}{3}+4=\frac{16}{3}.\)
Из пункта (а):
\(\left\{\begin{matrix} AN=AC+8=\displaystyle\frac{1}{2}P_{ABC} \, \left ( 1 \right ),\\ BK=BC+4=\displaystyle\frac{1}{2}P_{ABC}\, \left ( 2 \right ). \end{matrix}\right.\)
Отсюда \(BC=AC+4,\)
\(AC+8=\displaystyle \frac{1}{2}\left ( AB+AC+BC \right );\)
\(AC+8=\displaystyle \frac{1}{2}AB+\frac{1}{2}AC+\frac{1}{2}AC+\frac{1}{2}\cdot 4;\)
\(\displaystyle \frac{1}{2}AB=6;\, AB=12;\)
\(S_{\triangle ABC}=\displaystyle \frac{1}{2}AB \cdot CH=\frac{1}{2}\cdot \frac{16}{3}\cdot 12=32.\)
2. Точка \(O_1\) – центр вписанной окружности равнобедренного треугольника \(ABC\), а точка \(O_2\) – центр вневписанной окружности, касающейся основания \(BC\).
а) Докажем, что расстояние от середины отрезка \(O_1O_2\) до точки \(C\) вдвое меньше \(O_1O_2\).
б) Известно, что радиус первой окружности в пять раз меньше радиуса второй. В каком отношении точка касания первой окружности с боковой стороной треугольника делит эту сторону?
Решение:
а) Пусть \(M\) – середина отрезка \(O_1O_2\). Заметим, что \(CO_1\) и \(CO_2\) – биссектрисы внутреннего и внешнего угла при вершине \(C\). Значит, \(\angle O_{1}CO_{2}=90^{\circ}.\)
Тогда по свойству медиан прямоугольного треугольника \(CM=\displaystyle \frac{O_{1}O_{2}}{2}.\)
б) Пусть вписанная окружность касается стороны \(AB\) в точке \(K\), вневписанная окружность касается \(AB\) в точке \(N,\) а точка \(P\) – середина стороны \(BC\).
Тогда \(O_{2}N:O_{1}K=5:1=AN:AK.\)
Следовательно, \(AN=5AK, \; BP=BK=BN.\)
Таким образом, \(AK:KB=AK:\displaystyle \frac{AN-AK}{2}=AK:2AK=1:2.\)
Ответ: б) 1:2
3. Вневписанная окружность равнобедренного треугольника касается его боковой стороны.
а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на его основание.
б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?
Решение:
а) Пусть \(b\) – боковая сторона треугольника, \(c\) – его основание, \(h\) – высота, опущенная на основание треугольника.
Радиус вневписанной окружности вычисляется по формуле \(R=\displaystyle \frac{S}{p-a}\), где \(p\) – полупериметр треугольника, \(a\) – сторона, которой касается окружность.
Таким образом, \(R=\displaystyle \frac{\frac{hc}{2}}{\frac{c}{2}+b-b}=h.\)
б) Пусть \(O_{2}\) – центр вписанной окружности. Проведем радиус в точку касания \(H\). Треугольники \(AMC\) и \(CHO_{2}\) подобны по двум углам, поэтому \(\displaystyle \frac{CA}{CO_{2}}=\frac{CM}{CH}.\)
Так как \(R=h, \;\) то \(r=\displaystyle \frac{1}{4}\cdot h.\) Тогда \(CO_{2}=3r.\)
Найдем \(CH\) по теореме Пифагора. Получим, что \(CH=2\sqrt{2}r.\)
Тогда \(CA=\displaystyle \frac{CM\cdot CO_{2}}{CH}=\frac{4r\cdot 3r}{2\sqrt{2}r}=3\sqrt{2}r.\)
Откуда получим \(\displaystyle \frac{CH}{HA}=\frac{2\sqrt{2}r}{CA-CH}=\frac{2}{1}.\)
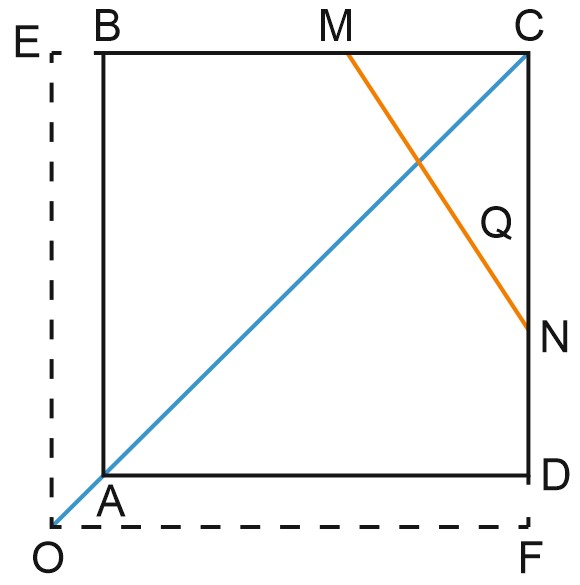
4. Дан квадрат \(ABCD\) со стороной \(7\). На сторонах \(BC\) и \(CD\) даны точки \(M\) и \(N\) такие, что периметр треугольника \(CMN\) равен \(14\).
а) Докажите, что \(B\) и \(D\) – точки касания вневписанной окружности треугольника \(CMN\), а ее центр находится в вершине \(A\) квадрата \(ABCD\).
б) Найдите угол \(MAN\).
Решение:
Вневписанная окружность – это окружность, касающаяся одной из сторон треугольника и продолжений его сторон. Центр \(O\) вневписанной окружности треугольника \(CMN\) равноудален от прямых \(CM, \; CN\) и \(MN\). Следовательно, \(O\) – точка пересечения биссектрисы угла \(MCN\) и биссектрис углов \(BMN\) и \(MND\) – внешний угол треугольника \(CMN\).
Поскольку угол \(MCN\) – прямой по условию и \(AC\) – диагональ квадрата \(ABCD\), получим, что \(O\in AC.\)
Пусть \(Q\) – точка касания вневписанной окружности и стороны \(MN\) треугольника \(CMN, \; E\) – точка касания этой окружности с прямой \(BC\), а \(F\) – точка касания с прямой \(CD\).
Докажем, что центр окружности \(O\) совпадает с вершиной квадрата \(A\), точка \(E\) совпадает с точкой \(B\), а \(F\) совпадает с \(D\).
Из точки \(M\) к окружности проведены касательные \(ME\) и \(MQ\). Отрезки касательных, проведенные к окружности из одной точки, равны, поэтому \(ME=MQ.\)
Аналогично, \(NQ=NF\). Заметим также, что \(CE=CF\) – как отрезки касательных, проведенных к окружности из точки \(C\).
Получим:
\(CE=CM+ME=CM+MQ;\)
\(CF=CN+NF=CN+NQ;\)
\(CE+CF=2CF=CM+CN+MN=P_{\triangle CMN}.\)
Мы получили, что отрезки \(CE\) и \(CF\) равны, и их сумма равна периметру треугольника \(CMN\), то есть \(14\).
Следовательно, \(CE=CF=7.\) Это значит, что точка \(E\) совпадает с точкой \(B\), а точка \(F\) совпадает с точкой \(D\).
Если точка \(O\) – центр окружности, касающейся прямых \(BC\) и \(CD\) в точках \(C\) и \(D\) соответственно, то \(OB\perp BC\) и \(OD\perp CD\). И это значит, что точка \(O\) совпадает с точкой \(A\) – вершиной квадрата.
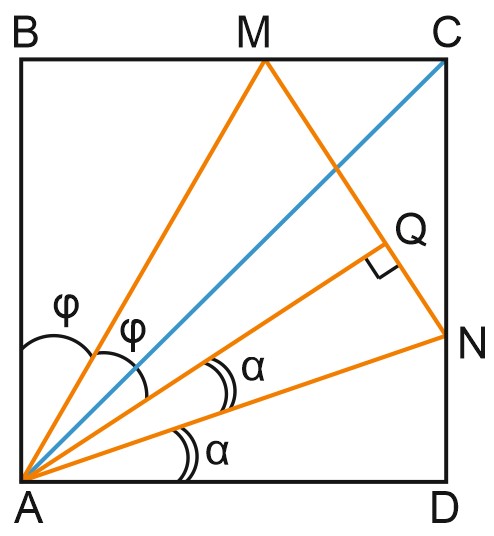
б) Пусть \(\angle BAM=\varphi .\)
Прямоугольные треугольники \(BAM\) и \(BQM\) равны. Гипотенуза \(AM\) в них – общая, \(MD=MQ\) как отрезки касательных, проведенных из одной точки.
Значит, \(\angle QAM=\angle BAM=\varphi .\)
Аналогично, трегольники \(QAN\) и \(DAN\) равны, \(\angle QAN=\angle DAN=\alpha .\)
\(\angle BAD=2\varphi +2\alpha =90^{\circ},\) значит, \(\varphi +\alpha =\angle MAN=45^{\circ}.\)
Ответ: 45.