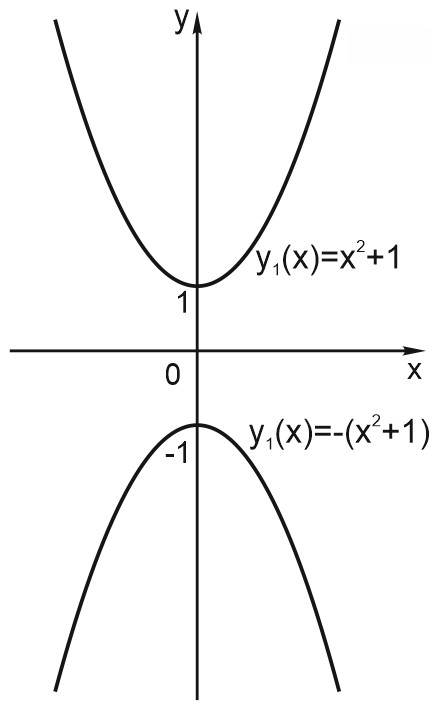Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси \(X\) или \(Y\).
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее постоянно не хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по \(X\) и по \(Y\).
1. Сдвиг по горизонтали.
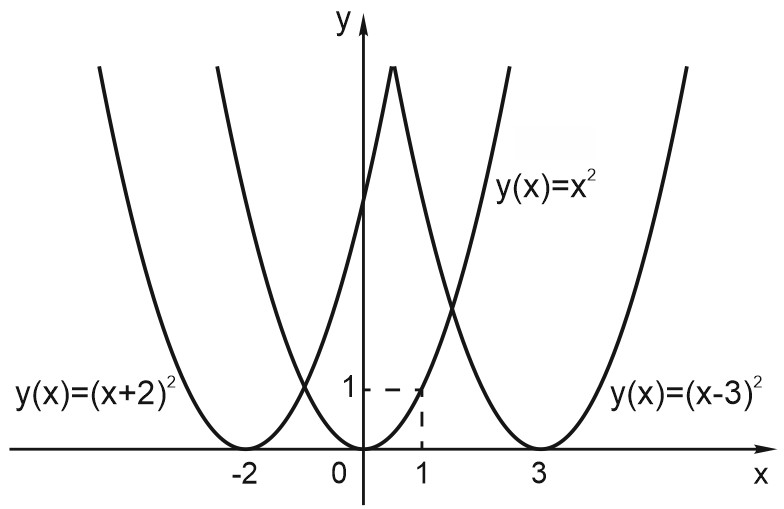
Пусть функция задана формулой \(y = f(x)\) и \(a> 0.\) Тогда график функции \(y = f(x - a)\) сдвинут относительно исходной на \(a\) вправо. График функции \(y = f(x + a)\) сдвинут относительно исходной на \(a\) влево.
2. Сдвиг по вертикали.
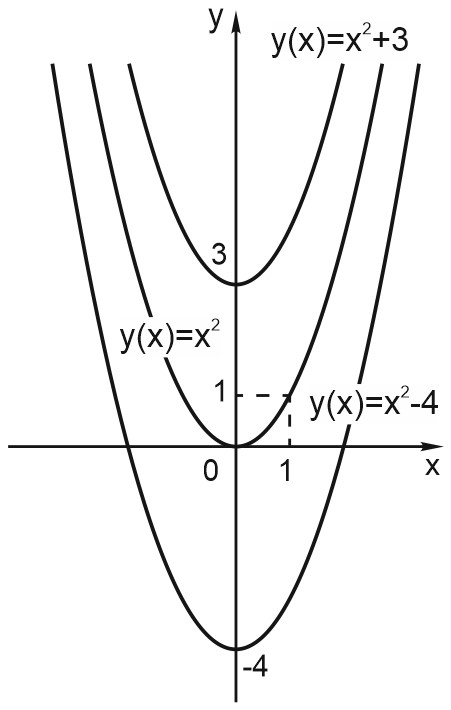
Пусть функция задана формулой \(y = f(x)\) и \(C\) — некоторое положительное число. Тогда график функции \(y = f(x) + C\) сдвинут относительно исходного на \(C\) вверх. График функции \(y = f(x) - C\) сдвинут относительно исходного на \(C\) вниз.
Теперь растяжение графика. Или сжатие.
3. Растяжение (сжатие) по горизонтали.
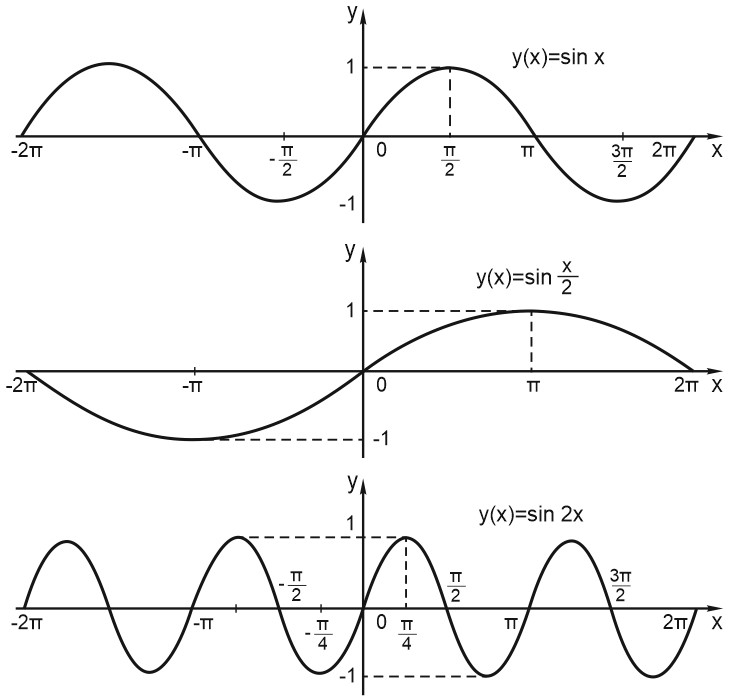
Пусть функция задана формулой \(y = f(x)\) и \(k> 0.\) Тогда график функции \(y = f(kx)\) растянут относительно исходного в \(k\) раз по горизонтали, если \(0< k< 1\), и сжат относительно исходного в \(k\) раз по горизонтали, если \(k> 1. \)
4. Растяжение (сжатие) по вертикали.
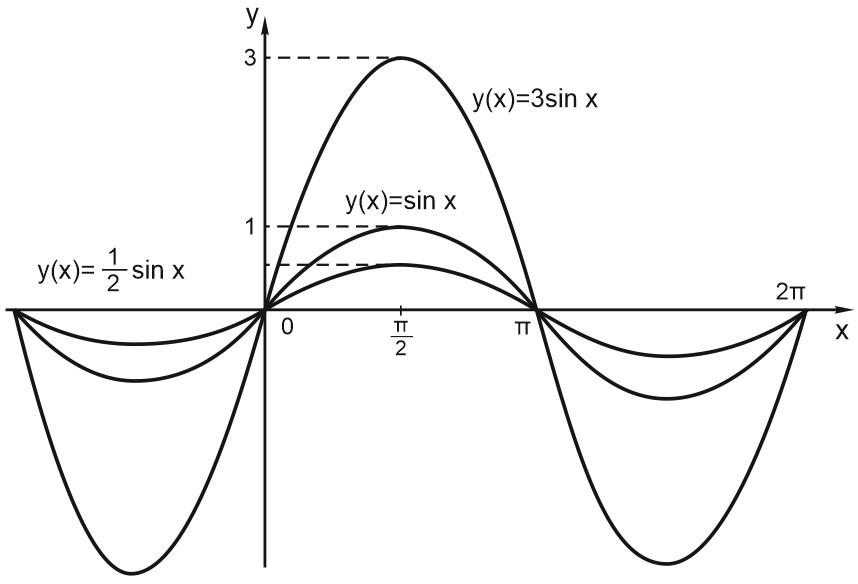
Пусть функция задана формулой \(y = f(x)\) и \(M> 0.\) Тогда график функции \(y = M\cdot f(x)\) растянут относительно исходного в \(M\) раз по вертикали, если \(M> 1\), и сжат относительно исходного в \(M\) раз по вертикали, если \(0 < M < 1.\)
И отражение по горизонтали.
5. Отражение по горизонтали.
График функции \(y = f(-x)\) симметричен графику функции \(y = f(x) \) относительно оси \(Y\).
6. Отражение по вертикали.
График функции \(y = - f(x)\) симметричен графику функции \(y = f(x)\) относительно оси \(X\).
Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
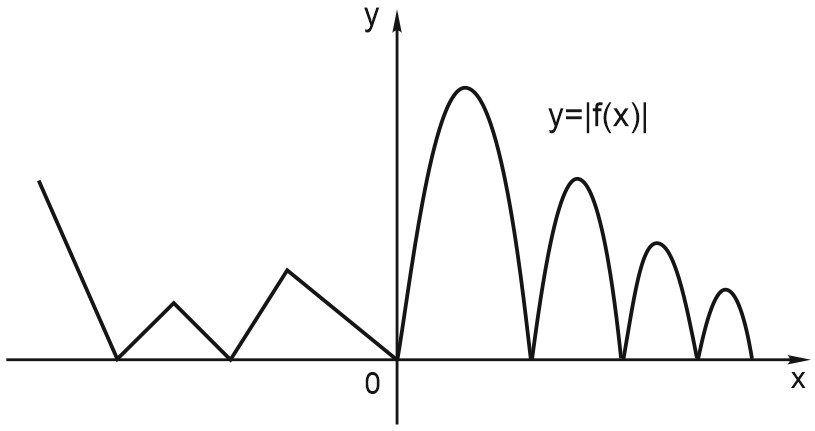
7. Графики функций \(y= f(|x|)\) и \(y=|f(x)|.\)
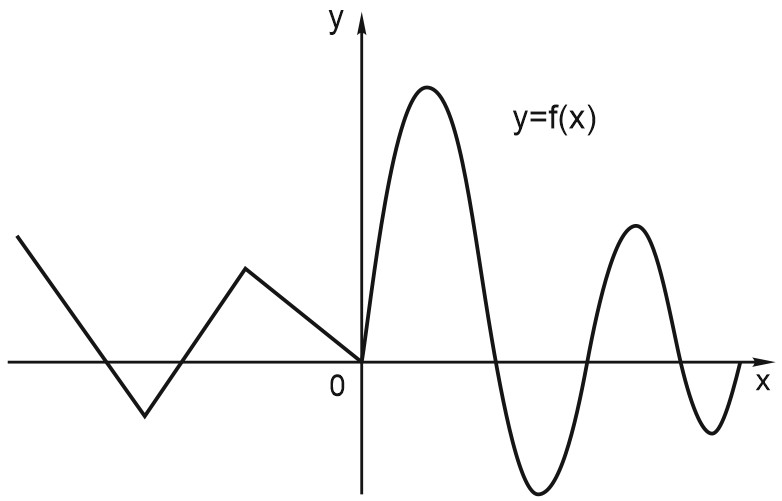
На рисунке изображен график функции \(y= f(x).\) Она специально взята такая — несимметричная относительно нуля.
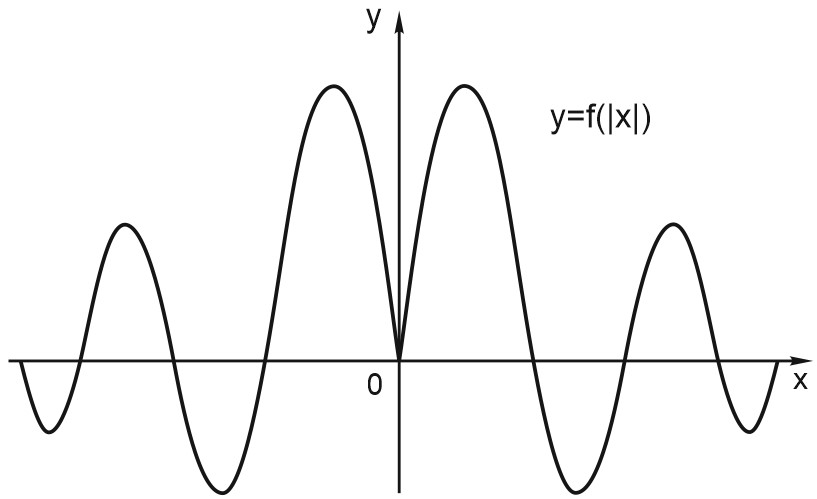
Построим график функции \(y= f(|x|).\)
Конечно же, мы пользуемся определением модуля.
\(\left| x\right|=\left\{\begin{matrix}
x, \; если \; x\geq 0, \\-x, \; если \; x< 0.
\end{matrix}\right.\)
Это мы и видим на графике. Для неотрицательных значений \(x\) график остался таким же, как был. А вместо каждого отрицательного \(x\) мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси \(X\), заменилась на зеркально отраженную правую часть графика.
Теперь график функции \(y= |f(x)|.\) Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси \(X\), зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси \(X\), остается на месте.
Как определить по формуле функции, будет график преобразован по горизонтали (по \(X\)) или по вертикали (по \(Y\))? Разница очевидна. Если сначала мы что-либо делаем с аргументом \(x\) (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по \(X\). Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по \(Y\).
Вот самые простые задачи на преобразование графиков.
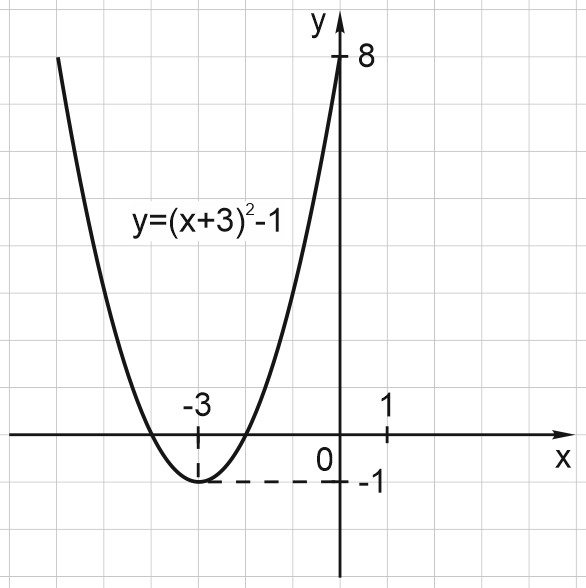
1. Построим график функции \(y={\left(x+3\right)}^2-1.\)
Решение:
Это парабола, сдвинутая на \(3\) влево по \(x\) и на \(1\) вниз по \(y\).
Вершина в точке \((-3; -1). \)
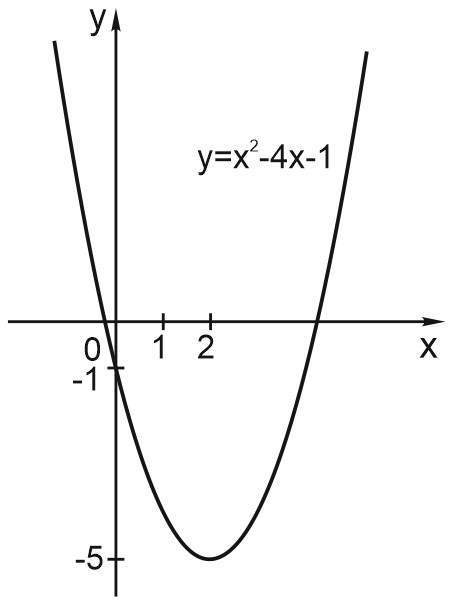
2. Построим график функции \(y=x^2-4x-1. \)
Решение:
Выделим полный квадрат в формуле.
\(y=x^2-4x+4-4-1=x^2-4x+4-5={\left(x-2\right)}^2-5. \)
График — парабола, сдвинутая на \(2\) вправо по \(x\) и на \(5\) вниз по \(y\).
Обратите внимание: график функции \(y=ax^2+bx+c\) пересекает ось \(y\) в точке \((0; c).\) На нашем графике это точка \((0; -1).\)
Продолжение — в статье «Построение графиков функций».