Построение графиков функций

Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она... мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, - линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.

Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».

Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».

Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».

Темы для повторения:

Понятие функции

Типы элементарных функций

Преобразования графиков функций

Производная функции

Асимптоты. Поведение функции в бесконечности

1. Построим график функции $y=\frac{x^2-1}{x+1}$

Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.

Упростим формулу функции:

$y=\frac{x^2-1}{x+1}=\frac{(x-1)(x+1)}{(x+1)}=x-1$ при $x\ne -1$

График функции — прямая $y=x-1$ с выколотой точкой $M (-1;-2).$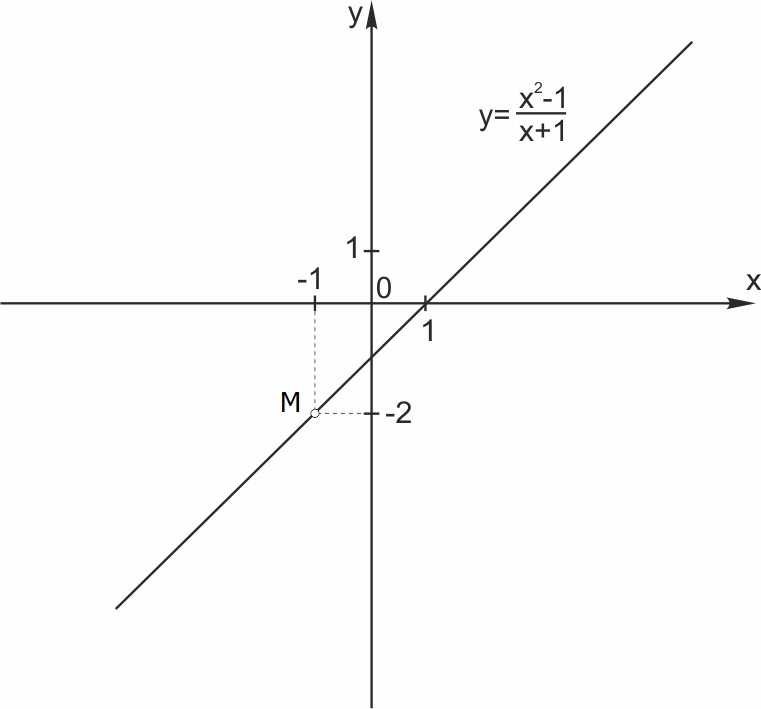

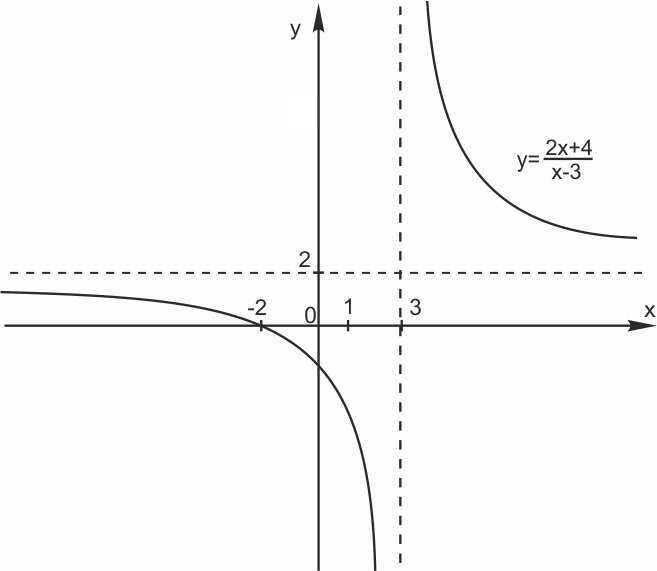
2. Построим график функции $y=\frac{2x+4}{x-3}$

Выделим в формуле функции целую часть:

$y=\frac{2x+4}{x-3}=\frac{2x-6+6+4}{x-3}=\frac{2(x-3)}{x-3}+\frac{10}{x-3}=2+\frac{10}{x-3}$

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции $y=\frac{1}{x}.$

Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.

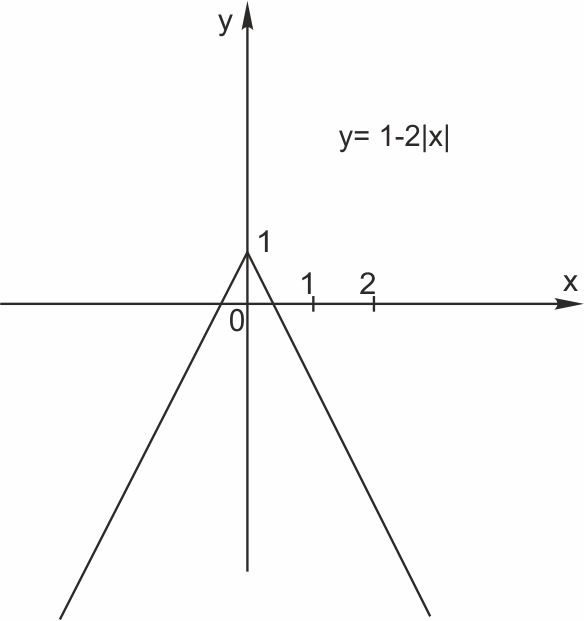
3. Построим график функции $y=1-2\left|x\right|$

Он получается из графика функции $y=|x|$ растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали

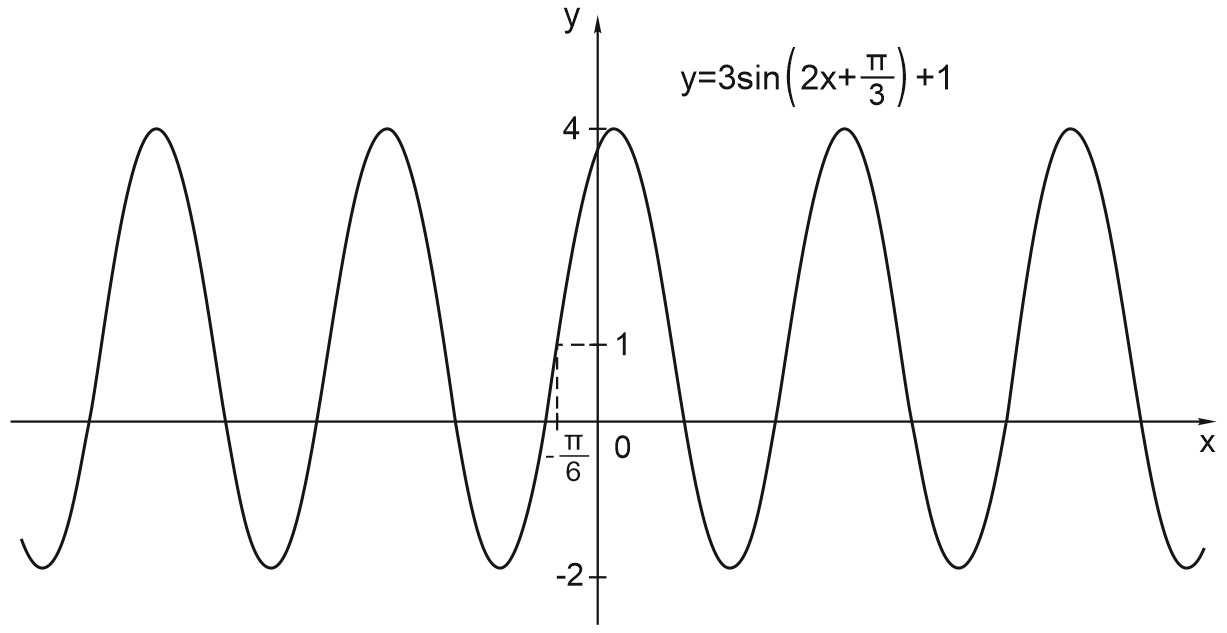
4. Построим график функции $y=3{sin \left(2x+\frac{ \pi }{3}\right)+}1$

Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:

$y=3{\sin 2\cdot \left(x+\frac{ \pi }{6}\right)+}1.$

Действуем по порядку:

1) График функции y=sinx сдвинем на $\frac{ \pi }{6}$ влево;

2) сожмем в 2 раза по горизонтали,

3) растянем в 3 раза по вертикали,

4) сдвинем на 1 вверх

Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».

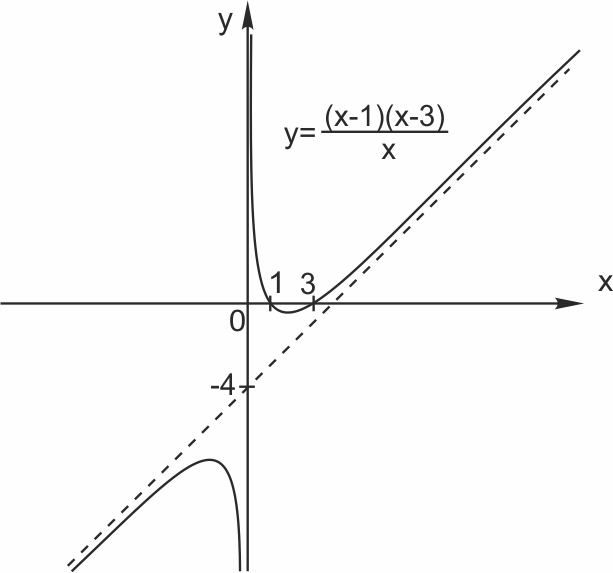
5. Построим график функции $y=\frac{(x-1)(x-3)}{x}$

Область определения функции: ${\rm x}\ne {\rm 0}$

Нули функции: $x = 1$ и $x = 3.$

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Прямая x = 0 (ось Y) — вертикальная асимптота функции. Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)

Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.

Раскроем скобки в формуле функции:

$y=\frac{(x-1)(x-3)}{x}=\frac{x^2-4x+3}{x}=x-4+\frac{3}{x}$

Если x стремится к бесконечности, то $\frac{3}{x}$ стремится к нулю. Прямая $y = x-4$ является наклонной асимптотой к графику функции.

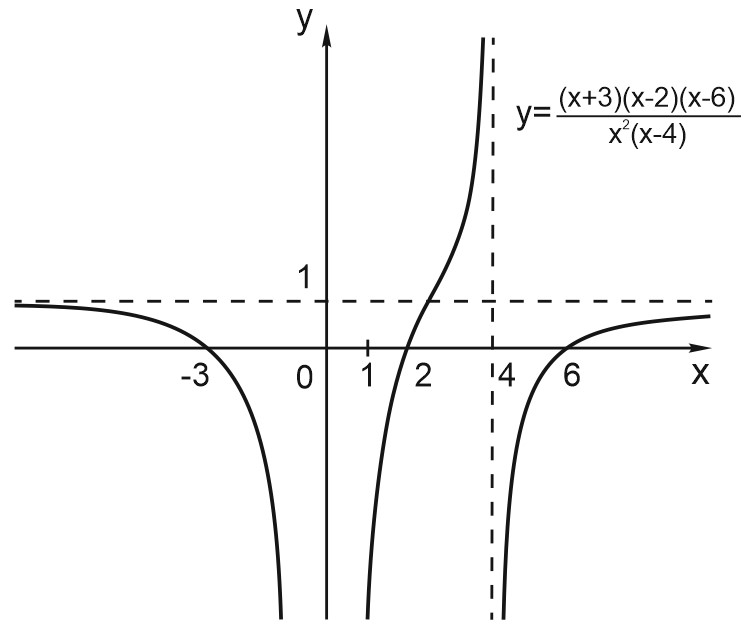
6. Построим график функции

$y=\frac{(x+3)(x-2)(x-6)}{x^2(x-4)}$

Это дробно-рациональная функция.

Область определения функции $D (y): {\rm x}\ne {\rm 4};{\rm x}\ne {\rm 0}.$

Нули функции: точки — 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: $x= 0, x = 4.$

Если x стремится к бесконечности, то у стремится к 1. Значит, $y = 1$ — горизонтальная асимптота.

Вот эскиз графика:

Еще один интересный прием — сложение графиков.

7. Построим график функции $y=x+\frac{1}{x}.$

Если x стремится к бесконечности, то $\frac{1}{x}$ стремится к нулю и график функции будет бесконечно близко подходить к наклонной асимптоте $y =x.$

Если x стремится к нулю, то функция ведет себя как $\frac{1}{x}.$ Это мы и видим на графике:

Вот мы и построили график суммы функций. Теперь график произведения!

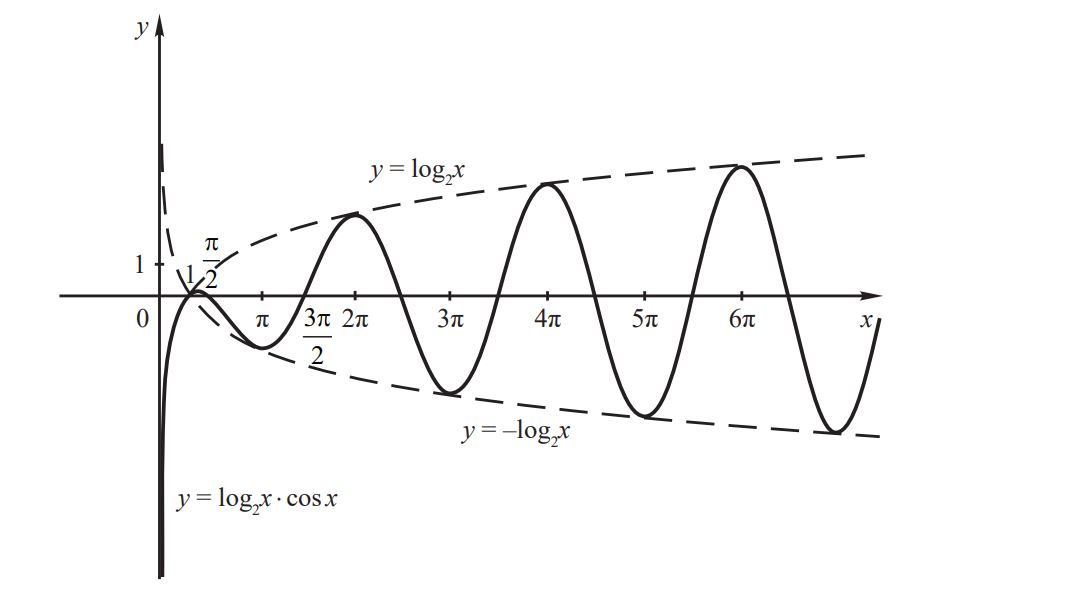
8. Построим график функции $y={{log}_2 x}{cos x} .$

Область определения этой функции — положительные числа, поскольку только для положительных x определен ${{log}_2 x}.$

Значения функции равны нулю при $x = 1$ (когда логарифм равен нулю), а также в точках, где ${cos x}=0,$ то есть при $x{\rm =}\frac{\pi }{{\rm 2}}{\rm +}\pi {\rm n}{\rm ,}$ ${\rm n}\in {\rm Z}.$

При $x{\rm =2}\pi {\rm n}{\rm ,}$ ${\rm n}\in {\rm Z},$ значение cos x равно единице. Значение функции в этих точках будет равно ${{log}_2 x},$ при $n\neq 0$

9. Построим график функции $y={\frac{sinx}{x} }.$

Функция определена при $x\ne 0.$ Она четная, поскольку является произведением двух нечетных функций $y=sin x$ и $y=\frac{1}{x}.$ График симметричен относительно оси ординат.

Нули функции — в точках, где ${sin x}=0,$ то есть при $x{\rm =}\pi {\rm n}{\rm ,}{\rm n}\in {\rm Z},$ при $n\neq 0.$

Если x стремится к бесконечности, $y=\frac{sinx}{x}$ стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное $\frac{sinx}{x}$ ?

Оказывается, что если x стремится к нулю, то ${\frac{sinx}{x} }$ стремится к единице. В математике это утверждение носит название «Первого замечательного предела».

А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.

10. Построим график функции $y=\frac{4x}{4+x^2}.$

Область определения функции — все действительные числа, поскольку $4+x^2 \textgreater 0.$

Функция нечетна. Ее график симметричен относительно начала координат.

При x=0 значение функции равно нулю. При $x \textgreater 0$ значения функции положительны, при $x \textless 0$ отрицательны.

Если x стремится к бесконечности, то $y=\frac{4x}{4+x^2}=\frac{4}{\frac{4}{x}+x}$ стремится к нулю.

Найдем производную функции $y=\frac{4x}{4+x^2}.$
По формуле производной частного, $\left(\frac{u}{v}\right)^{$

$y^{$

$y^{$ если $x=2$ или $x=-2.$

В точке $x=-2$ производная меняет знак с «минуса» на «плюс», $x=-2$ — точка минимума функции.

В точке $x=2$ производная меняет знак с «плюса» на «минус», $x=2$ — точка максимума функции.

Найдем значения функции при x=2 и при x=-2.

$y\left(2\right)=1, y\left(-2\right)=-y\left(2\right)=-{\rm 1.}$

Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?

Общая схема построения графика функции:

1. Область определения функции

2. Область значений функции

3. Четность — нечетность (если есть)

4. Периодичность (если есть)

5. Нули функции (точки, в которых график пересекает оси координат)

6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).

7. Асимптоты (если есть).

8. Поведение функции в бесконечности

9. Производная функции

10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.

Графики функций с модулями

Покажем полезные примеры построения графиков модулей функций. Такие графики с модулями встречаются на ЕГЭ в задачах с параметрами.

11. Построим графики функций:

а) $y=-x^2+6x-8$

б) $y=|-x^2+6x-8|$

в) $y=-x^2+6|x|-8$

Решение:
а) Первый график построить легко. Выделим полный квадрат в формуле функции $y=-x^2+6x-8.$

$y=-x^2+6x-8=-(x^2-6x+8)=-(x^2-6x+9-1)=-(x-3)^2+1.$

График – квадратичная парабола, сдвинутая на 3 влево и на 1 вверх и перевернутая ветвями вниз.

б) Чтобы построить график функции $y=|-x^2+6x-8|,$ зеркально отражаем относительно оси Х те части первого графика, которые лежали под ней. А та часть первого графика, которая лежала выше оси Х, остается на месте. Точки (2; 0) и (4; 0), в которых график пересекал ось Х, также остаются на месте.

в) Теперь график функции $y=-x^2+6|x|-8.$

Он тоже получается из графика первой функции, но преобразования другие. Часть первого графика, лежащая справа от оси Y, остается на месте. Действительно, модуль неотрицательного числа равен самому этому числу. Получили график функции для неотрицательных . И отражаем его зеркально относительно оси Y в левую полуплоскость.

12. Построим график функции $y=\left||x|-2\right|.$

Функция определена при всех действительных х.

Нули функции: $x=-2; x=2$

Функция получается из элементарной функции $y=|x|$ в результате следующих преобразований:

1) Сдвиг на 2 единицы вниз,
2) Отражение части графика, лежащей ниже оси ОХ, в верхнюю полуплоскость. Стандартный прием при построении графика модуля функции.

13. Построим график функции $\left|\frac{6}{x}-5\right|.$

Ее график получается из графика функции $y=\frac{6}{x}$ сдвигом на 5 единиц вниз вдоль оси ОУ и симметричным отображением части графика, лежащей ниже оси ОХ, в верхнюю полуплоскость.

$x=0$ – вертикальная асимптота графика, $y=5$ - горизонтальная асимптота.

Построение графиков функций

Графики функций с модулями

Это полезно