Найти все значения \(b,\) при каждом из которых уравнение
\( {(2x-x^2)}^2-4\sqrt{2x-x^2}=b \)
имеет хотя бы один корень.
Решение:
ОДЗ уравнения: \(2x-x^2\ge 0\). Это значит, что \(x\left(2-x\right)\ge 0\) и \(0\le x\le 2.\)
Сделаем замену: \( \sqrt{2x-x^2}=t. \)
Очевидно, что \(\ t\ge 0.\) Посмотрим, какие еще есть условия для \(t\).
Пусть \(\ z\left(x\right)=2x-x^2.\ \) Легко показать, что \(z_{max}\left(x\right)=z\left(1\right)=1\)
Значит, при \(0\le x\le 2\) функция \(z\left(x\right) \) принимает значения от 0 до 1, \(0\le z\left(x\right)\le 1,\) и тогда \(t\in \left[0; 1\right]\).
Переформулируем условие задачи для переменной t.
При каких значениях параметра b уравнение
\( t^4-4t=b \)
имеет хотя бы один корень на отрезке \(t\in \left[0; 1\right]?\)
Решим графически уравнение
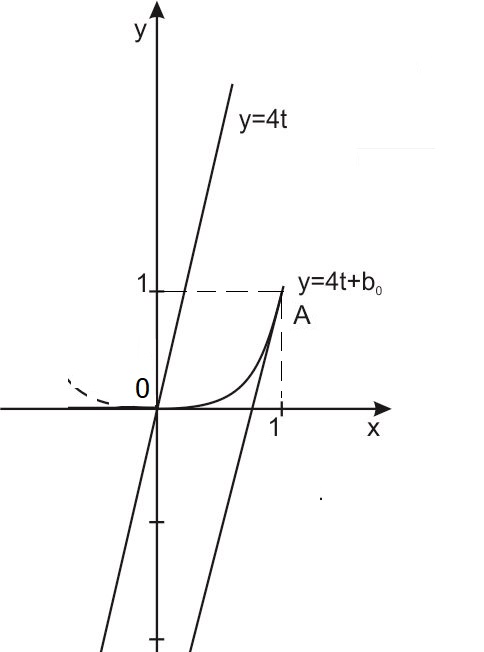
\(t^4=4t+b\). Левая часть уравнения - степенная функция. Правая часть - прямая с угловым коэффициентом равным 4, сдвинутая на b по оси Y.
Уравнение имеет хотя бы один корень на отрезке \(t\in \left[0;1\right],\ \)если графики функций \(y=t^4 \) и \( y=4t+b \) имеют на этом отрезке хотя бы одну общую точку.
Если \(b = 0,\) прямая \(y=4t \) проходит через начало координат, как и парабола \({y=t}^4.\)
Пусть А - точка касания графиков функций \({y=t}^4\) и \(y=4t+b.\)
Условия касания графика функции \(y=f(x)\) и прямой \(y=kx+b\) в точке \(x_0 \) записываются в виде системы уравнений:
\( \left\{\begin{matrix}
f\left(x_0\right)=kx+b\ \ \ \ \ \ \ \\
f' \left(x_0\right)=k \end{matrix}
\right. \)
В нашем случае условие касания:
Получим, что \(t=1\) - точка касания.
Если \( t=1, \) то \(b_0=-3.\)
Мы получили, что если \(-3\le b\le 0,\ \ \) то прямая \( y=4t+b\) имеет хотя бы одну общую точку с графиком функции \( y=t^4.\) Это значит, что исходное уравнение имеет хотя бы один корень.
Ответ: \(-3\leq b \leq 0.\)