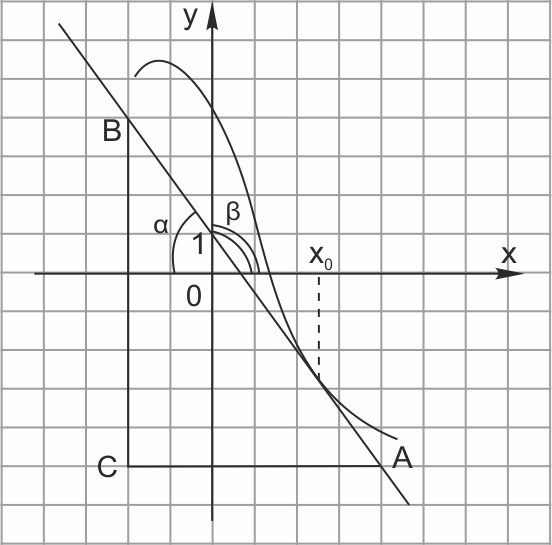
На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0.\) Найдите значение производной функции \(f(x)\) в точке \(x_0.\)
Решение:
Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке (и угловому коэффициенту касательной).
\(f'\left(x\right)=tg\beta=k.\)
В точке \(x_0\) функция \(y=f(x)\) убывает. Касательная, проведенная к ее графику в этой точке, образует тупой угол \(\beta \) с положительным направлением оси Х. Найдем тангенс острого угла \(\alpha \), смежного с углом \(\beta \), из прямоугольного треугольника АВС на рисунке.
\(\alpha+\beta=180{}^\circ\)
\(tg\beta=-tg\alpha=\ -1,5.\)
Ответ: - 1,5