Условие задачи
Дальность полета \(L\) мяча, брошенного под углом \(\alpha\) (\(0^{\circ}< \alpha < 90^{\circ}\)) к горизонту, зависит от начальной скорости \(v_{0}\) и угла \(\alpha\) по закону \(L=0,1v_{0}^{2}sin2\alpha \), где \(L\) измеряется в метрах, а \(v_{0}\) в метрах в секунду. Определить, при каком максимальном значении \(\alpha\) дальность полета будет не меньше 5 метров, если начальная скорость мяча составляет 10 метров в секунду. Ответ дать в градусах.
Решение
Подставив значения величин в формулу для дальности полета, получим неравенство: \(\sin 2\alpha \geq \displaystyle \frac{1}{2}.\)
Как решить такое неравенство? Ошибка, которую многие допускают, – «превращают» его в уравнение и получают неверный ответ \(\alpha =15^{\circ}. \)
Правильно будет воспользоваться тригонометрическим кругом (или же графиком функции \(y=\sin 2\alpha \)). Давайте нарисуем тригонометрический круг, обозначив \(2\alpha =t,\) и решим неравенство \(\sin t \geq \displaystyle \frac{1}{2}.\)
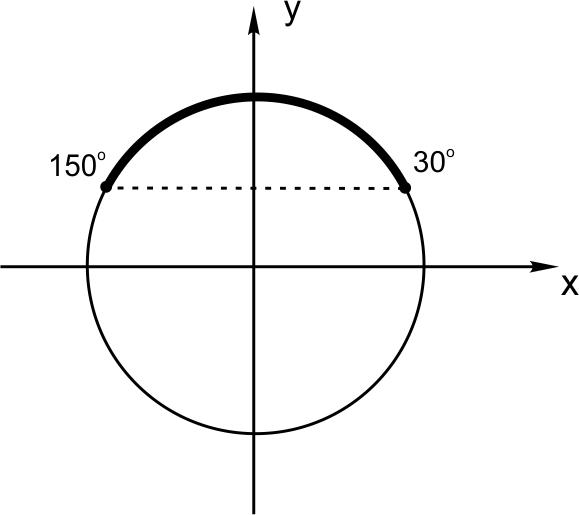
Отсюда с учетом возможного диапазона угла \(\alpha \) получаем \(30 ^{\circ}\leq2\alpha \leq 150^{\circ}.\) Значит, максимальное значение \(\alpha \) равно 75 градусов.
Ответ:
75.






























