Условие задачи
Имеется два сплава. Первый сплав содержит 5% меди, второй — 13% меди. Масса вторoго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение
Это классическая задача на сплавы.
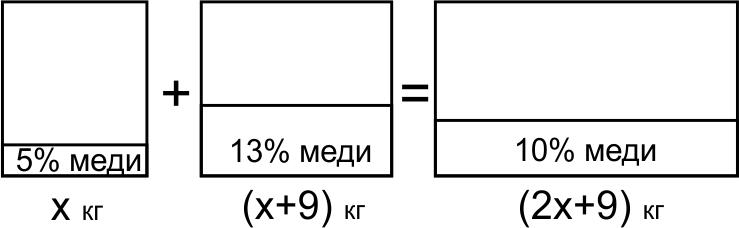
Обозначим массу первого сплава \(x.\) Тогда масса второго сплава \(x+9\), а масса третьего \(2x+9.\)
Масса меди в первом сплаве \(0,05x.\) Во втором сплаве \(0,13(x+9)\), а в третьем \(0,1(2x+9).\)
Составим уравнение для массы меди:
\(0,05x+0,13(x+9)=0,1(2x+9).\)
Заметим, что с целыми коэффициентами в уравнениях удобнее работать, чем с дробными. Умножим обе части уравнения на 100.
\(5x+13(x+9)=10(2x+9).\) Решая его, получим, что \(2x=27\) и \(2x+9=36.\) Это масса третьего сплава.
Ответ:
36.






























