Решение. Задание 13, Вариант 2

Условие задачи

Авторская задача
а) Решите уравнение $5(1-tg^{2}x)+(12sin x-7)(1+tg^{2}x)=0$

б) Найдите все его решения на отрезке $[-2\pi; 0 ]$

Решение

ОДЗ уравнения: $\cos x\neq 0$

Поделим обе части уравнения на $1+tg^{2} x$ . Это выражение положительно всегда, когда $\cos x\neq 0$ , и на него можно делить.

$5\cdot \displaystyle \frac{1-tg^{2}x}{1+tg^{2}x}+(12\sin x-7)=0$

Вспомним полезные формулы, которые носят название «Универсальная тригонометрическая замена»:

$\sin 2x= \displaystyle \frac{2\textup{tg}x}{1+tg^{2}x};$

$\cos 2x=\displaystyle \frac{1-tg^{2}x}{1+tg^{2}x}$

Получим:

$5\cos 2x+12\sin x-7=0$

Используем формулу

$cos2x=1-2 sin^{2}x$ :

$5-10\sin ^{2}x+12\sin x-7=0$

$5\sin ^{2}x-6\sin x+1=0$

$\left[ \begin{gathered} \sin x=1 \\ \sin x=\frac{1}{5} \end{gathered} \right.$

Серия решений,для которой $\sin x=1$ , не входит в ОДЗ. Ведь если $\sin x=1,$ то $\cos x=0.$ Остается серия решений $\sin x=\displaystyle \frac{1}{5}.$
Ответ в пункте (а): $x=(-1)^n\arcsin \frac{1}{5}+\pi n, n\in Z$

б) Отберем корни на отрезке $[-2\pi; 0 ]$

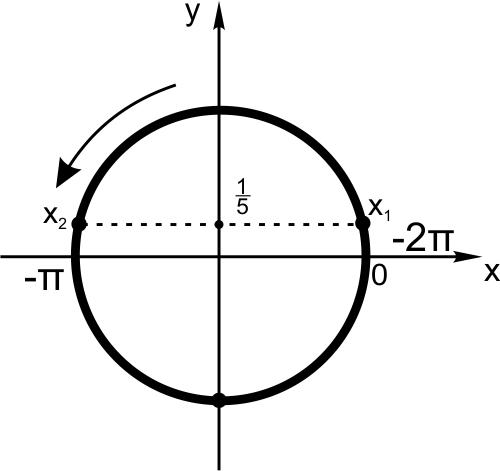
Отметим на тригонометрическом круге точки, для которых $\sin x=\displaystyle \frac{1}{5}.$ Это
$x_1=\arcsin \frac{1}{5}+2\pi n$ и $x_2=\pi -\arcsin \frac{1}{5}+2\pi n, n\in Z$
Наш отрезок начинается с точки $-2\pi.$ Значит, ему принадлежат точки
$x_1=\arcsin \displaystyle \frac{1}{5}-2\pi$ и $x_2=-\pi -\arcsin \displaystyle \frac{1}{5}.$

Ответ:

а) $x=(-1)^n\arcsin \frac{1}{5}+\pi n, \ n\in Z$

б) $x_1=\arcsin \frac{1}{5}-2\pi ;$

$x_2=-\pi -\arcsin \frac{1}{5}$

Интенсивная подготовка

Бесплатные пробные ЕГЭ

Расписание курсов

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)
+7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

Узнать больше