Условие задачи
а) Решите уравнение: \(16cos^4 x-24cos^2 x+9=0.\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([2π;3π].\)
Решение
Сделаем замену: \(cos^2 x=z; \ z\geq 0.\)
\(16z^2-24z+9=0.\)
Левая часть уравнения – полный квадрат.
\((4z-3)^2=0;\)
\(cos^{2}x=\displaystyle \frac{3}{4}\Leftrightarrow \left[\begin{matrix}
cosx=\displaystyle \frac{\sqrt{3}}{2}, \\cosx=-\displaystyle \frac{\sqrt{3}}{2}.
\end{matrix}\right.\)
Чтобы записать серии решений, отметим на тригонометрическом круге точки, где \(cosx=\pm \displaystyle \frac{\sqrt{3}}{2}.\)
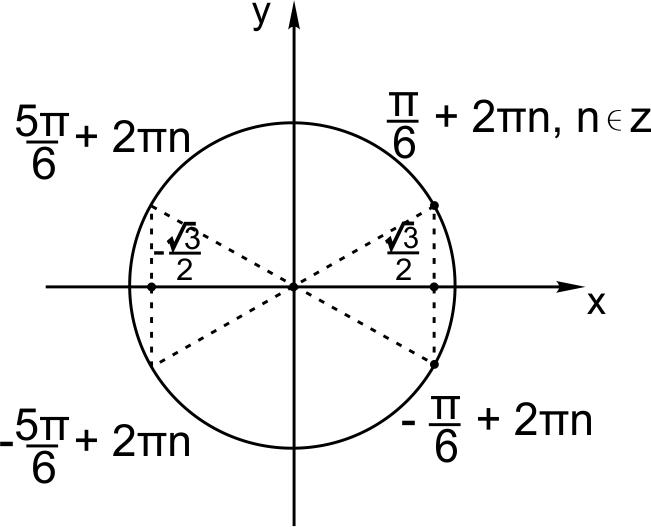
Видим, что ответ в пункте (а) можно записать в виде двух диаметральных пар:
\(\left[\begin{matrix}
x=-\displaystyle \frac{\pi }{6}+\pi n, \ n\in z,\\x=\displaystyle \frac{\pi }{6}+\pi n.
\end{matrix}\right. \)
б) Найдем решение на отрезке \([2π;3π].\)
Этот отрезок соответствует половине тригонометрического круга, которая начинается с точки \(2π.\)
Следовательно, на этом отрезке находятся точки \(x=\displaystyle \frac{\pi }{6}+2\pi =\frac{13\pi }{6}\) и \(x=\displaystyle \frac{5\pi }{6}+2\pi =\frac{17\pi }{6}\), принадлежащие нашим сериям решений.
Ответ:
a) \(x=\pm \displaystyle \frac{\pi }{6}+\pi n, \ n\in z. \)
б) \(\displaystyle \frac{13\pi }{6}; \ \frac{17\pi }{6}.\)




























