Условие задачи
В треугольнике \(ABC\) точки \(A_{1}, \ B_{1}\) и \(C_{1}\) — середины сторон \(BC, \ AC\) и \(AB\) соответственно, \(AH\) — высота, \(\angle BAC=60^{\circ}, \ \angle BCA=45^{\circ}.\)
а) Докажите, что точки \(A_{1}, \ B_{1}, \ C_{1}\) и \(H\) лежат на одной окружности.
б) Найдите \(A_{1}H\), если \(BC = 2\sqrt{ 3}.\)
Решение
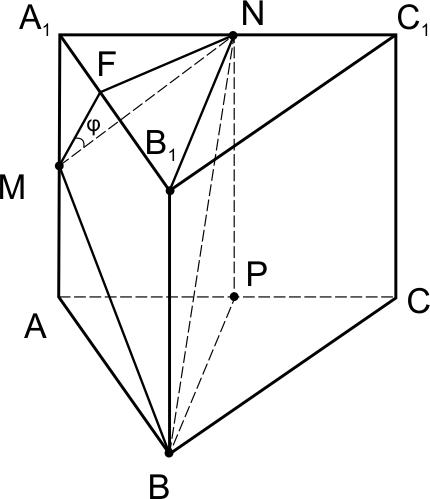
а) Покажем, что \(\angle BMN=90^{\circ}.\)
Пусть точка \(P\) – середина \(AC.\)
В плоскости \(BNP\) проведем отрезок \(BN.\)
Рассмотрим треугольник \(BMN\), из которого можно найти угол \(BMN.\)
Сначала найдём \(MN, \ BM\) и \(BN\) – стороны этого треугольника.
\(\triangle ABC\) правильный, \(BP\) – его высота, \(BP=\displaystyle \frac{6\sqrt{3}}{2}.\)
Из \(\Delta BPN: \ BN^2=BP^2+NP^2=\displaystyle \frac{36\cdot 3}{4}+36=36\cdot \displaystyle \frac{7}{4}=63.\)
Из \(\Delta A_{1}MN: \ MN^2=A_{1}M^2+A_{1}N^2=18,\) поскольку \(A_{1}M=NA_{1}=3.\)
Из \(\Delta ABM: \ BM^2=AB^2+AM^2=36+9=45.\)
Для треугольника \(BMN\) выполняется теорема Пифагора: \(BN^{2}= MN^{2}+BM^{2}.\) Значит, он прямоугольный.
б) Найдем угол \(\varphi\) между плоскостями \( BMN\) и \(ABB_{1}.\)
Угол между плоскостями – это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
Плоскости \(BMN\) и \(ABB_{1}\) пересекаются по прямой \(BM\), причем в пункте (а) мы доказали, что \(MN\perp BM.\) В плоскости \(ABB_{1}\) построим \(FM\perp BM.\)
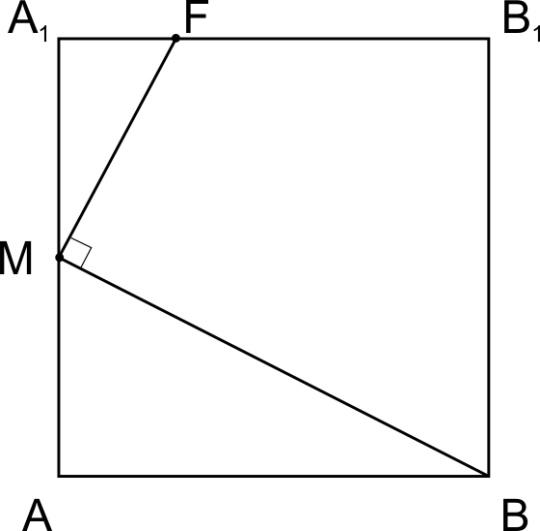
Заметим, что \(\Delta ABM\sim A_{1}MF, \; \displaystyle \frac{A_{1}F}{AM}=\displaystyle \frac{AM}{AB},\) значит, \( A_{1}F= \displaystyle \frac{1}{4} A_{1} B_{1}.\)
Отрезок \(NF\) равен половине высоты правильного треугольника \(A_{1}B_{1}C_{1}, \; NF=\displaystyle \frac{1}{2}\cdot \frac{6\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}.\)
\(NF\perp A_{1}B_{1}.\)
Кроме того, отрезок \(NF\) лежит в плоскости верхнего основания призмы, которая перпендикулярна боковому ребру \(AA_{1}.\)
Значит, \(NF\perp AA_{1}.\)
Поскольку \(NF\) перпендикулярен двум пересекающимся прямым \(AA_{1}\) и \(BA_{1}\), лежащим в плоскости \(AA_{1}B_{1}\), получим: \(NF\perp AA_{1}B_{1}.\)
Тогда \(NF\perp FM; \; \triangle NFM\) – прямоугольный,
\(sin\varphi =\displaystyle \frac{NF}{MN}=\displaystyle \frac{3\sqrt{3}}{2\cdot 3\sqrt{2}}=\displaystyle \frac{\sqrt{3}}{2\sqrt{2}}=\sqrt{\displaystyle \frac{3}{8}};\)
\(\varphi =\arcsin \sqrt{\displaystyle \frac{3}{8}}.\)
Ответ:
б) \(\displaystyle \varphi =\arcsin \sqrt{\frac{3}{8}}.
\)






























