Условие задачи
Решите неравенство: \(\displaystyle \frac{2}{7^x-7}\geq \displaystyle \frac{5}{7^x-4}.\)
Решение
\(\displaystyle \frac{2}{7^x-7}\geq \frac{5}{7^x-4}.\)
Сделаем замену переменной:
\(7^x=t,\ t>0.\)
\(\displaystyle \frac{2}{t-7}- \frac{5}{t-4}\geq 0;\)
\(\displaystyle \frac{2t-8-5t+35}{(t-7)(t-4)} \geq 0;\)
\(\displaystyle \frac{27-3t}{(t-7)(t-4)} \geq 0;\)
\(\displaystyle \frac{27-3t}{(t-7)(t-4)} \geq 0;\)
\(\displaystyle \frac{t-9}{(t-7)(t-4)} \leq 0.\)
Обратите внимание, что возвращаться к переменной \(x\) еще рано. Сначала решим неравенство с переменой \(t\) методом интервалов:
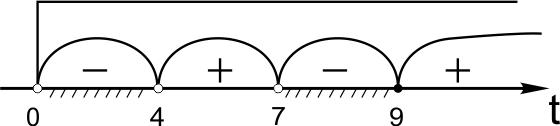
Поскольку \(t>0,\) получим:
\(\left[\begin{gathered}t<4,\\7<t\leq9.\\\end{gathered}\right.\)
Тогда \(\left[\begin{gathered}7^4<4,\\7<7^x\leq9;\\\end{gathered}\right. \; \left[\begin{gathered}7^4<7^{log_74},\\7^1<7^x\leq7^{log_79}.\\\end{gathered}\right.\)
Посмотрите, как мы представили 4 и 9 в виде степеней с основанием 7. Мы применили основное логарифмическое тождество.
\(\left[\begin{gathered}x<log_74,\\1<x\leq log_79.\\\end{gathered}\right.\)
Ответ:
\(x\in (-\infty ; \log_7{4}) \cup (1; \log_7{9}].\)






























