Условие задачи
(ЕГЭ-2017) На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.
а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6?
б) Может ли ровно одно число на доске оканчиваться на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?
Решение
а) Предположим, что из 30 чисел на доске 15 чисел оканчиваются на двойку, а другие 15 – на шестерку. Сумма 15 чисел, в каждом из которых последняя цифра – двойка, оканчивается на 0. Аналогично и с теми, что оканчиваются на шестерку – их сумма также оканчивается на ноль. Тогда сумма всех чисел на доске никак не может быть равна 2454. Получили противоречие! Ответ в пункте (а) – нет, не может.
б) Предположим, что на доске ровно одно число, которое оканчивается на 6.
Кроме него, на доске есть также 29 различных чисел, в которых последняя цифра – двойка. Какой может быть сумма этих 29 чисел?
Ясно, что она не меньше, чем сумма 29 чисел вида 2, 12, 22, 32… – то есть не меньше, чем сумма 29 членов арифметической прогрессии с разностью 10 и \(a_1= 2\).
Сумма 29 членов такой прогрессии \(S_{n} =\displaystyle \frac{1}{2}\cdot (2\cdot 2 + 10\cdot 28) \cdot 29 = 4118\). Значит, сумма 29 чисел, оканчивающихся на двойку, не меньше 4118, но это больше, чем сумма всех 30 чисел в условии задачи.
Мы снова пришли к противоречию. Получается, на доске не может быть ровно одного числа, оканчивающегося на 6.
в) Какое же наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?
Пусть на доске \(n\) чисел, в которых последняя цифра – шестерка (их сумма равна \(S_1\)), и \(30-n\) чисел, в которых последняя – двойка (их сумма равна \(S_2\) ). Ясно, что наименьшими \(S_1\) и \(S_2\) будут в случае, если это числа вида:
6, 16, 26, 36… и 2, 12, 22, 32…
Имеем: \(S_1 \geq \displaystyle \frac{1}{2}(6\cdot 2 + 10 (n-1)) \cdot n, \)
\(S_2 \geq \displaystyle \frac{1}{2} (2\cdot 2 + 10 (30-n-1 )) \cdot (30-n).\)
При этом \(S_1+ S_2 = 2454.\)
\(\displaystyle \frac{1}{2}(6\cdot 2+10(n-1))\cdot n+\frac{1}{2}(2\cdot 2+10(29-n))\cdot (30-n)\leq 2454;\)
\(n+5n^2+4410-297n+5n^2\leq 2454;\)
\(5n^2-148n+978\leq 0.\)
Рассмотрим уравнение \(5n^2-148n+978= 0:\)
\(D=148-4\cdot 5\cdot 978=4\cdot 586;\)
\(2\cdot \sqrt{576}< \sqrt{D}< 2\cdot \sqrt{625};\)
\(48< \sqrt{D}< 50.\)
Оценим наименьшее возможное \(n\) при условии, что \(n\) – целое.
Вспомним, как выглядят решения неравенства вида \(ax^2+bx+c\leq 0.\)
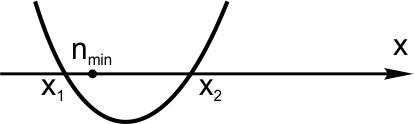
\(n_{min}\geq x_1; \) то есть
\(n_{min}\geq \displaystyle \frac{148-2\sqrt{586}}{10};\)
\(n_{min}\geq \displaystyle \frac{74-\sqrt{586}}{5}> \frac{74-\sqrt{625}}{5}, \) то есть \(n_{min}> \displaystyle \frac{74-25}{5}.\)
\(n_{min}> 9,8\) тогда \(n_{min}\geq10.\)
Но что будет, если \(n=10\)? Тогда на доске 10 чисел, которые оканчиваются на 6, и 20 чисел, которые оканчиваются на 2. Сумма всех тридцати чисел в этом случае оканчивается на ноль, и это противоречит условию. Значит, \(n\geq 11.\)
Мы оценили \(n\). Осталось привести пример, когда \(n=10\), то есть на доске 11 чисел, которые оканчиваются на 6, и 19 чисел, в которых последняя цифра – двойка.
Для того чтобы количество чисел, оканчивающихся на двойку, было максимальным, возьмем числа 2, 12, 22, 32… 182, и тогда сумма этих 19 чисел, образующих арифметическую прогрессию, равна 1748.
Значит, сумма чисел, которые оканчиваются на 6, равна \(2454 – 1748 = 706\).
Возьмем числа 6, 16, 26, 36… 106.
Сумма этих одиннадцати чисел равна 616. Добавим к последнему из них 90. Получим:
2, 12, 22, 32… 182, 6, 16, 26, 36… 196. Это пример.
Заметим, что когда мы в экзаменационной работе используем метод «Оценка плюс пример», мы не обязаны объяснять, как получили пример. Надо просто его привести.
Ответ:
а) Нет.
б) Нет.
в) 11 чисел, оканчивающихся на 6. Например 2, 12, 22, 32… 182, 6, 16, 26, 36… 96, 196.






























