Условие задачи
На рисунке изображен график производной некоторой функции \(y=f(x)\), определенной на интервале \((-6;6).\) В какой точке отрезка \([1; 3]\) функция \(y=f(x)\) принимает наименьшее значение?
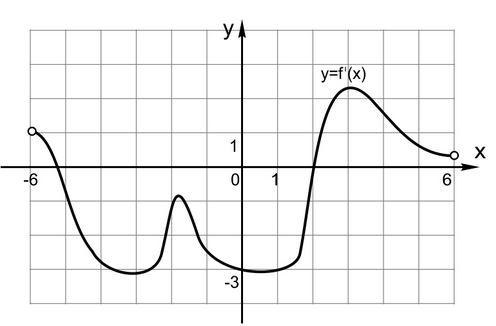
Решение
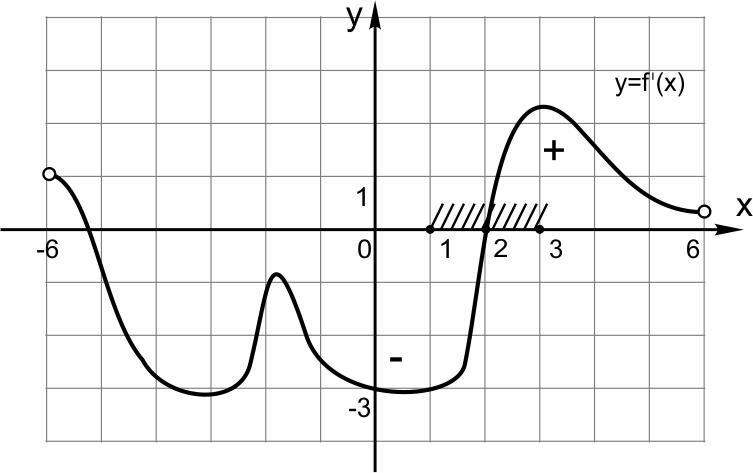
Типичная ловушка для невнимательных абитуриентов. На рисунке изображен график производной, а вопрос задан о наименьшем значении функции. В концах интервала функция не определена. Значит, наименьшее значение она может принимать только в точке минимума.
Мы знаем, что в точке минимума производная равна нулю и меняет знак с «минуса» на «плюс». С помощью рисунка находим эту точку: \(x=2.\)
Ответ:
2.






























