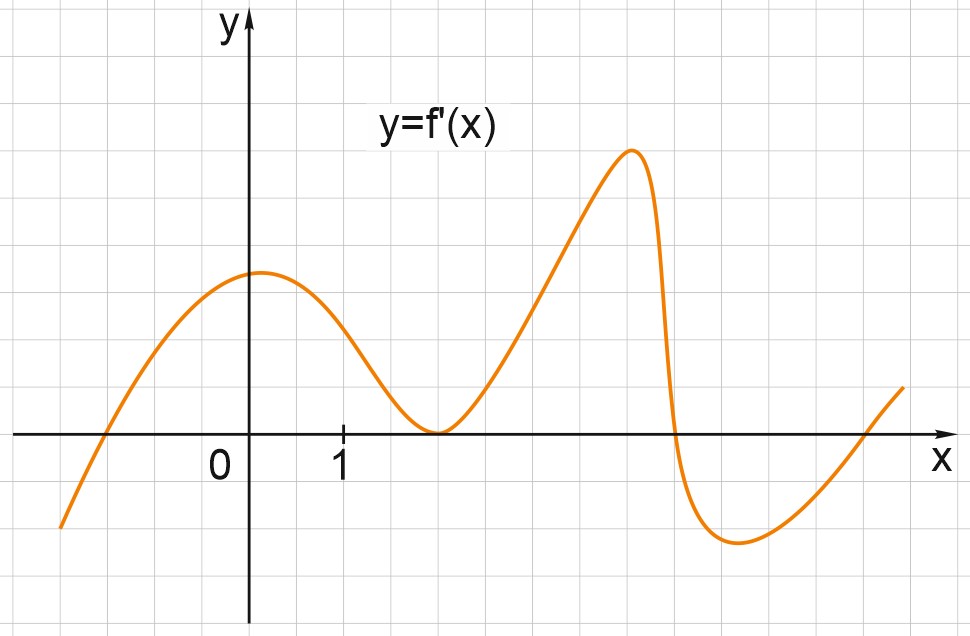Видеоразбор: https://www.youtube.com/watch?v=QUMfQwd_Rr0&t;t\&t=439s
и https://www.youtube.com/watch?v=tqjQ5SpT8rc;t\&t=1s
Часть 1. Задания с кратким ответом
1. В треугольнике \(ABC\) угол \(A\) равен 60°, угол \(B\) равен 82°. \(AD\), \(BE\) и \(CF\) — биссектрисы, пересекающиеся в точке \(O\). Найдите угол \(AOF\). Ответ дайте в градусах.
2. Даны векторы \( \overrightarrow{a}=(3; 1)\), \( \overrightarrow{b}=(2;-3)\) и \( \overrightarrow{c}=(-2; 1)\). Найдите значение выражения \((\overrightarrow{a}-\overrightarrow{b})\cdot\overrightarrow{c}\).
3. Анна Малкова
Диаметр апельсина равен 10 см. Диаметр апельсина без кожуры равен 8 см. Сколько процентов от объема апельсина занимает кожура? Апельсин (в кожуре и без нее) считать шарообразным.
4. Александра Антонова
В шкафу Деда Мороза вперемешку лежат все его 9 шапок, а также случайно оказавшаяся там шапочка Снегурочки. 31 декабря Дед Мороз, опаздывая на детский утренник, наугад надевает первую попавшуюся шапку. Найдите вероятность того, что он возьмет не свою шапку.
5. Анна Малкова
Студент Василий заметил, что если он в новогоднюю ночь загадывает желание, то оно сбывается с вероятностью 0,4. Маша сказала, что у нее загаданные в новогоднюю ночь желания сбываются с вероятностью 0,8.
Маша и Василий договорились в новогоднюю ночь загадать по 7 желаний.
Во сколько раз вероятность того, что у Маши исполнится ровно 6 желаний, больше вероятности того, что у Василия исполнится ровно 5 желаний? Ответ округлите до сотых.
6. Решите уравнение: \(|x^2-2x|=|x+4|\). Если корней несколько, в ответе запишите их сумму.
7. Вычислите: \(lg(\frac{8\cdot 100^{2,4}}{2^{5,8}\cdot 5^{2,8}})\).
8. Анна Малкова
На рисунке изображен график \(y=f'(x)\) - производной функции \(y=f(x)\). В какой точке отрезка [1;5] функция \(y=f(x)\) принимает наибольшее значение?
9. Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела \(P\), измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвертой степени температуры: \(P=\sigma ST^4\), где \(\sigma =5,7\cdot 10^{-8}\) — постоянная, площадь \(S\) измеряется в квадратных метрах, а температура \(T\) — в градусах Кельвина. Известно, что некоторая звезда имеет площадь \(S=\frac{1}{16}\cdot 10^{20}\) м², а излучаемая ею мощность \(P\) не менее \(9,12\cdot 10^{25}\) Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
10. Анна Малкова
В ожидании Нового Года Дед-Мороз и Санта Клаус затеяли гонки по круговой орбите вокруг Земли. Длина окружности, по которой они летают, составляет 33 тыс. км.
Первым стартует (на оленях) Санта Клаус. Через 30 часов из той же точки следом за ним вылетает (на тройке лошадей) Дед-Мороз. Через 10 часов после старта он в первый раз догоняет Санта Клауса, а еще через 44 часа догоняет во второй раз. Найдите скорость Деда Мороза. Ответ выразите в км/ч.
11. Анна Малкова
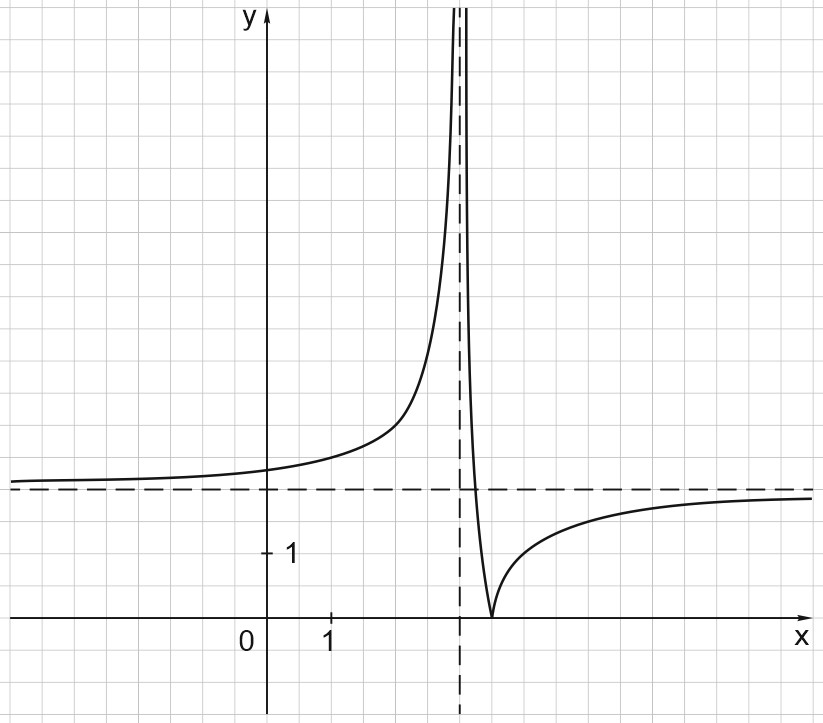
На рисунке изображен график функции \(y=|\frac{a-cx+bc}{x-b}|\), где \(a, b, c\) - целые, \(a>0\).
Найдите \(y(28)\).
12. Анна Малкова
Найдите наибольшее значение функции \(y=8-16 sin^2 \frac{x}{3}\) на отрезке \( [\frac{\pi}{2};\pi]. \)
Часть 2. Задания с развернутым ответом
13. Анна Малкова
а) Решите уравнение: \(\frac{2+cos 2x-3cos x}{\sqrt{9-25 cos^2 x}}=0\)
б) Найдите все корни уравнения на отрезке \([-\frac{3 \pi}{2};\frac{\pi}{3}].\)
14. В правильной четырёхугольной пирамиде \(SABCD\) боковое ребро \(SA\) равно \(\sqrt{5}\), а высота \(SH\) пирамиды равна \(\sqrt{3}\). Точки \(M\) и \(N\) — середины рёбер \(CD\) и \(AB\) соответственно, \(NT\) — перпендикуляр из точки \(N\) на плоскость \(SCD\).
а) Докажите, что точка \(T\) является серединой \(SM\).
б) Найдите расстояние между прямыми \(NT\) и \(SC\).
15. Кирилл Буйлов
Решите неравенство: \(log_2((x+5)(x^2-7x+6))+log_2(\frac{9-x}{x^2-7x+6})\leqslant log_2 x+3\).
16. Анна Малкова
1 сентября 2019 года в заповеднике обитало 256 криворогих оленей. Известно, что в течение года численность популяции криворогих оленей увеличивается в среднем на 25% (за счет естественного прироста). Кроме того, биологи собираются до 2 сентября 2023 года увеличить количество оленей в заповеднике не менее чем до 1000 и для этого 1 сентября 2020, 2021, 2022 и 2023 года будут завозить в заповедник одинаковое количество новых оленей. Какое наименьшее количество оленей им придется завозить в заповедник ежегодно?
17. В четырехугольнике \(ABCD\) противоположные стороны не параллельны. Диагонали четырехугольника \(ABCD\) пересекаются в точке \(O\) под прямым углом и образуют 4 подобных треугольника, у каждого из которых одна из вершин – точка \(O\).
а) Докажите, что вокруг четырехугольника \(ABCD\) можно описать окружность
б) Найдите радиус вписанной окружности, если \(AC = 10\), \(BD = 26\).
18. Найдите все значения параметра \(a\), при каждом из которых система уравнений имеет ровно 3 различных решения:
\(\left\{\begin{matrix}
(x-4)^2+(y-4)^2=9 \\
y=|x-a|+1\end{matrix}\right.\)
19. В некотором царстве было несколько (более двух) княжеств. Однажды некоторые из этих княжеств объявили себя царствами и разделились каждое на то же самое число княжеств, которое было в самом начале. Затем всё новые и новые княжества из числа прежних и вновь образующихся объявляли себя царствами и делились каждое на то же самое число княжеств, которое было в самом начале.
а) Могло ли сразу после одного из делений общее число княжеств стать равным 102?
б) Могло ли в какой‐то момент времени общее число княжеств стать равным 320, если известно, что сразу после одного из делений общее число княжеств было равно 162?
в) Сколько княжеств было в самом начале, если сразу после какого‐то из делений общее число княжеств стало ровно в 38 раз больше первоначального?
Посмотреть решения задач варианта 4.