Анна Малкова
Теорема Менелая
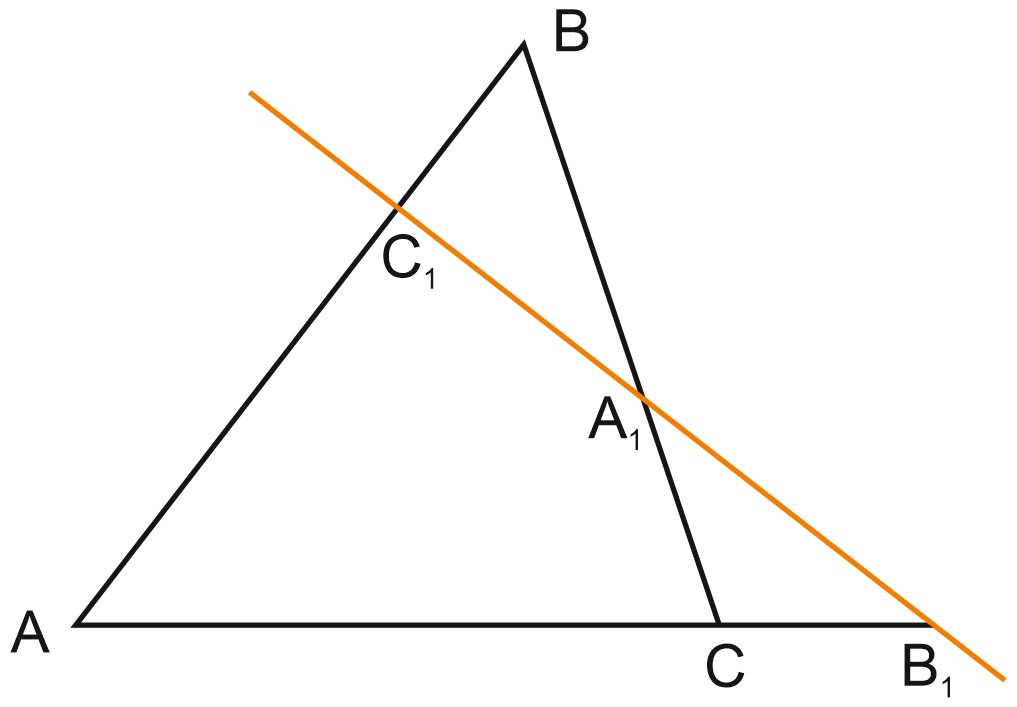
Пусть прямая пересекает произвольный треугольник \(ABC,\) причем \(C_1\) – точка ее пересечения со стороной \(AB,\) \(A_1\) – точка ее пересечения со стороной \(BC,\) и \(B_1\) – точка ее пересечения с продолжением стороны \(AC.\)
Тогда выполняется равенство: \(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A} = 1.\)
Как это запомнить? Сначала рисуем треугольник \(ABC.\) Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки \(C_1, A_1\) и \(B_1,\) причем на стороне \(AB\) должна лежать точка \(C_1,\) на стороне \(BC\) – точка \(A_1\) и на продолжении \(AC\) – точка \(B_1.\)
Затем записываем равенство так, как будто «обходим» весь треугольник \(ABC,\) от точки \(A\) к точкам \(B\) и \(C,\) и затем возвращаемся в точку \(A.\) Но по дороге нам встречаются точки \(C_1, A_1\) и \(B_1\) – их тоже включаем в формулу.
Один из учащихся нашей ЕГЭ-Студии предложил такое мнемоническое правило: пусть точки \(A, B\) и \(C\) – это города, а точки \(C_1, A_1\) и \(B_1\) – заправки, где можно пополнить запас бензина. Тогда правило звучит так: «Едем из города в город, заезжаем на заправку!» Возможно, вы придумаете свое правило : -)
В некоторых задачах полезна обратная теорема Менелая.
Пусть дан треугольник \(ABC.\) Предположим, что точка \(C_1\) лежит на стороне \(AB,\) точка \(A_1\) лежит на стороне \(BC,\) а точка \(B_1\) лежит на продолжении стороны \(AC,\) причём про эти точки известно, что
\(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A} = 1.\)
Тогда эти точки лежат на одной прямой.
Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек \(A, \, B\) и \(C\) выполняется равенство: \(AB + BC = AC\) – то это означает, что точка \(B\) лежит на отрезке \(AC.\) Или, если нам удается доказать, что угол \(ABC\) – развернутый, это и будет означать, что точки \(A, \, B\) и \(C\) лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае \(A_1, \, B_1\) и \(C_1\) – лежат на одной прямой.
Теорема Чевы
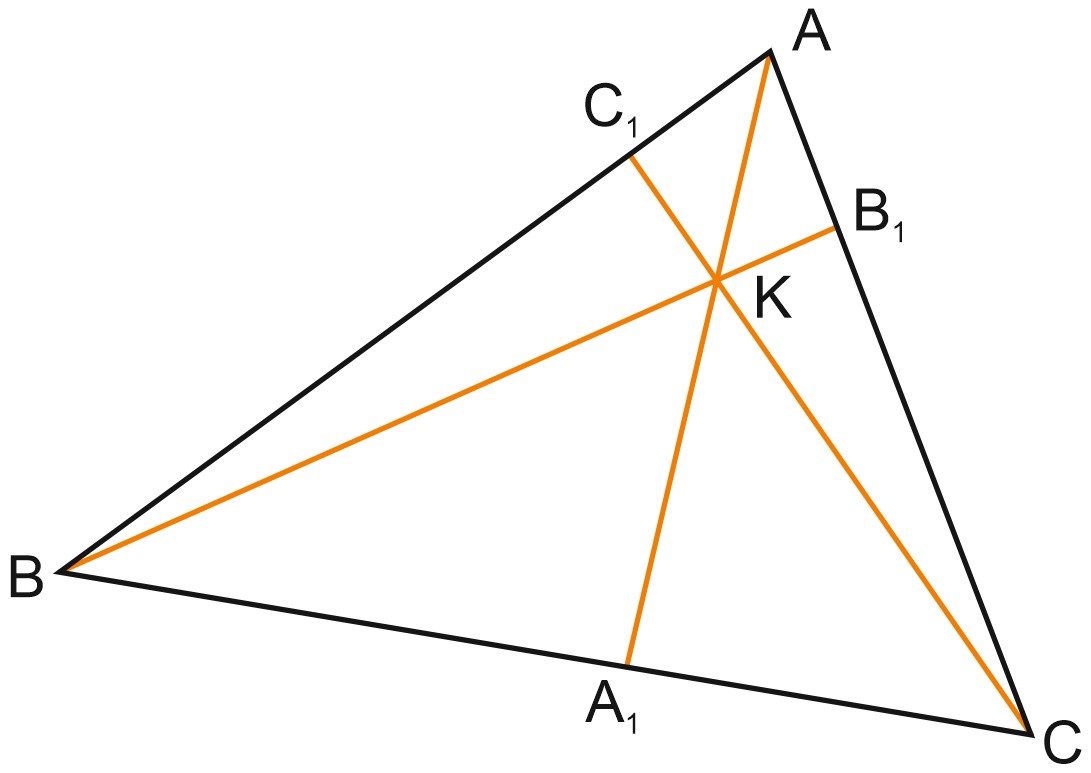
Пусть точки \(A_1, \, B_1\) и \(C_1\) лежат соответственно на сторонах \(BC, \, AC\) и \(AB\) треугольника \(ABC,\) причем отрезки \(AA_1, \, BB_1\) и \(CC_1\) пересекаются в одной точке. В этом случае выполняется равенство:
\(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A} = 1.\)
Пусть точки \(A_1, \; B_1, \; C_1\) лежат соответственно на сторонах \(BC, \; AC\) и \(AB\) треугольника \(ABC,\) причём
\(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A} = 1.\)
Тогда отрезки \(AA_1, \, BB_1\) и \(CC_1\) пересекаются в одной точке.
Как применяются теоремы Менелая и Чевы?
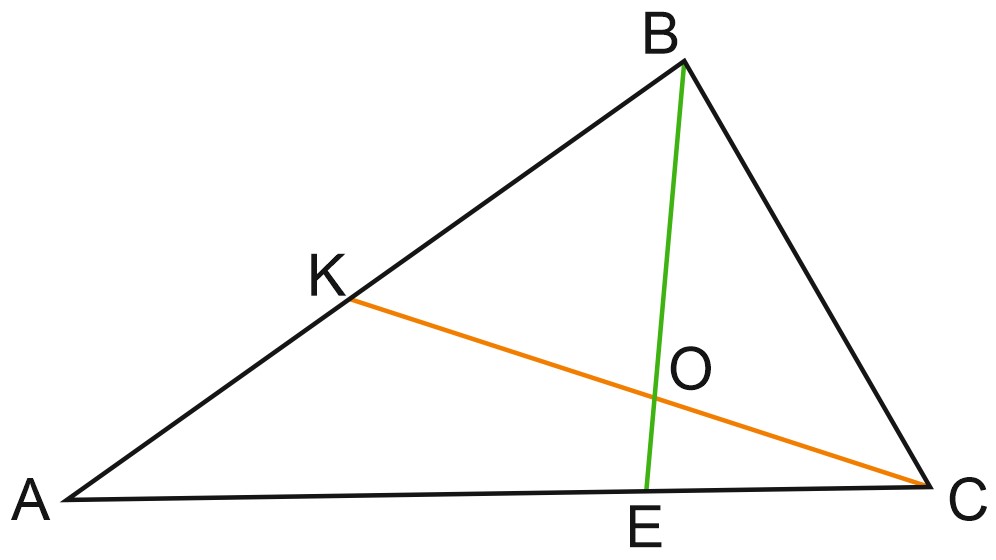
1. В треугольнике \(ABC\) на стороне \(AB\) расположена точка \(K\) так, что \(AK:KB=3:5\). На отрезке \(AC\) взята точка \(E\) так, что \(AE=2CE\). Известно, что прямые \(BE\) и \(CK\) пересекаются в точке \(O\). Найдите площадь треугольника \(ABC\), если площадь треугольника \(BOC\) равна \(20\).
Решение:
Запишем теорему Менелая для треугольника \(ABE\) и прямой \(KC\). Начинаем от вершины \(A\). Помните правило? «Едем из города в город, заезжаем на заправку».
\(\displaystyle \frac{AK}{KB}\cdot \displaystyle \frac{BO}{OE}\cdot\frac{CE}{AC} =1.\)
По условию, \(AE=2CE.\) Тогда \(CE:AC=1:3.\)
\(\displaystyle \frac{3}{5}\cdot \frac{BO}{OE}\cdot\frac{1}{3} =1.\)
Треугольники \(BOC\) и \(OEC\) имеют равную высоту, проведенную к основаниям \(BO\) и \(OE\). Значит, площадь треугольника \(BOC\) в \(5\) раз больше площади треугольника \(OEC\).
Тогда площадь треугольника \(OEC\) равна \(20:5=4\), и площадь треугольника \(BEC\) равна \(24\).
Площадь треугольника \(BEC\) в \(3\) раза меньше площади треугольника \(ABC\), так как \(EC=\displaystyle \frac{1}{3}AC.\)
Площадь треугольника \(ABC\) равна \(24\cdot 3 =72.\)
Ответ: 72.
Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.
2. На сторонах \(AB, \, BC\) и \(AC\) треугольника \(ABC\) отмечены точки \(C_1, \, A_1\) и \(B_1\) соответственно, причём \(AC_1 : C_1B = 8 : 3, \; BA_1 : A_1C = 1 : 2, \; CB_1 : B_1A = 3 : 1.\) Отрезки \(BB_1\) и \(CC1\) пересекаются в точке \(D.\)
а) Докажите, что \(ADA_1B_1\) — параллелограмм.
б) Найдите \(CD,\) если отрезки \(AD\) и \(BC\) перпендикулярны, \(AC = 28, \, BC = 18.\)
Докажем пункт (а) с помощью теорем Менелая и Чевы:

Пусть \((AD) \cap BC = A_2.\)
По теореме Чевы,
\(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BA_2}{A_2C} \cdot \frac{CB_1}{B_1A} = 1;\)
\(\displaystyle \frac{8}{3} \cdot \frac{BA_2}{A_2C} \cdot \frac{3}{1} = 1.\)
\(\displaystyle \frac{BA_2}{A_2C} = \frac{1}{8},\) тогда
\(\displaystyle BA_2 = \frac{1}{9}BC;\)
\(\displaystyle A_2A_1 = \left ( \frac{1}{3} - \frac{1}{9} \right ) BC = \frac{2}{9}BC.\)
\(\displaystyle A_1C = \frac{2}{3}BC,\) тогда \(\displaystyle A_2A_1 = \frac{1}{3}A_1C;\)
\(\displaystyle A_1C : A_2C = B_1C : AC = \frac{3}{4}.\)
Это значит, что \(\triangle A_1CB_1 \sim \triangle A_2CA\) по углу и двум сторонам, тогда \(AA_2 \parallel B_1A_1,\) то есть \(AD \parallel B_1A_1.\)
Рассмотрим треугольник \(ABB_1.\)
Прямая \(C_1C\) пересекает две его стороны и продолжение третьей стороны \(AB_1.\)
По теореме Менелая,
\(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BD}{DB_1} \cdot \frac{B_1C}{AC} = 1;\)
\(\displaystyle \frac{8}{3} \cdot \frac{BD}{DB_1} = \frac{3}{4} = 1;\)
\(\displaystyle \frac{BD}{DB_1} = \frac{1}{2} = \frac{BA_1}{A_1C};\)
тогда \(\displaystyle \frac{BD}{BB_1} = \frac{BA_1}{BC} = \frac{1}{3}.\)
\(\triangle BDA_1 \sim \triangle BB_1C\) по углу и двум сторонам, отсюда
\(\angle BDA_1 = \angle BB_1C, \; DA_1 \parallel B_1C.\)
Мы получили:
\(AD \parallel B_1A_1;\)
\(DA_1 \parallel AB_1, \, ADA_1B_1\) — параллелограмм по определению.
Мы доказали то, что требовалось в пункте (а).
Но что делать, если теоремы Менелая и Чевы вы не проходили в школе? Ничего страшного, докажем без теорем Менелая и Чевы. Их легко заменят подобные треугольники.
Обозначим
\(AC_1 = 8x, \, BC_1 = 3x,\)
\(BA_1 = y, \, A_1C = 2y,\)
\(AB_1 = z, \, B_1C = 3z.\)
Докажем, что \(ADA_1B_1\) — параллелограмм.
Пусть \(K\) — середина \(AC.\)
Тогда \(AK = KC = 2z, \, B_1K = z.\)
Тогда \(\triangle A_1CK \sim \triangle BCB_1\) по углу и двум пропорциональным сторонам,
\(A_1K \parallel BB_1. \)
Проведём \(AN \parallel BB_1.\)
По теореме Фалеса \(BN = y.\)
Пусть \(CC_1 \cap AN = P.\)
\(\triangle APC_1 \sim \triangle BDC_1\) по двум углам;
\(\displaystyle \frac{AP}{BD} = \frac{AC_1}{BC_1} = \frac{8}{3}.\)
Пусть \(AP = 8k,\)
\(BD = 3k.\)
\(\triangle B_1CD \sim \triangle ACP\) по 2 углам, \(\displaystyle \frac{AP}{B_1D} = \frac{AC}{B_1C} = \frac{4}{3},\)
тогда \(\displaystyle B_1D = \frac{3}{4}AP = 6k,\)
\(\displaystyle \frac{BD}{B_1D} = \frac{1}{2}.\)
Это значит, что \(\triangle BDA_1 \sim \triangle BB_1C\) по углу и двум сторонам и \(A_1D \parallel AC.\)
При этом \(\displaystyle A_1D = \frac{1}{3}B_1C = z = AB_1.\)
Получим, что в четырёхугольнике \(ADA_1B_1:\)
\(AB_1 \parallel A_1D;\)
\(AB_1 = A_1D.\)
Значит, \(ADA_1B_1\) — параллелограмм.
Как видим, эти решения примерно одного уровня сложности.
А вот в пункте (б) нет необходимости применять теоремы Чевы и Менелая. Он легко решается с помощью обычной школьной геометрии.
б) Найдём \(CD\), если \(AD \perp BC, \, AC = 28, \, BC=18.\)
Поскольку \(A_1B_1 \parallel AD, \) получим, что \(A_1B_1 \perp BC, \, \triangle A_1B_1C\) — прямоугольный.
Мы доказали в пункте (а), что \(B_1DA_1C\) — трапеция, причём \(B_1A \perp A_1C.\)
По условию, \(AC = 28.\)
Тогда \(\displaystyle A_1D = \frac{28}{4} = 7,\)
\(\displaystyle B_1C = \frac{28}{4} \cdot 3 = 21,\)
\(\displaystyle A_1C = \frac{2}{3}BC = \frac{2}{3} \cdot 18 = 12.\)
Пусть \(M \in B_1C, \, CM = 7, \, B_1M = 28.\)
Тогда \(A_1MCD\) — параллелограмм (по признаку параллелограмма).
\(A_1M = CD.\)
\(B_1M = 28,\) по теореме Пифагора из \(\triangle B_1A_1C:\)
\(\displaystyle B_1A_1 = \sqrt{21^2-12^2} = 3 \sqrt{7^2 - 4^2} = 3 \sqrt{33},\)
\(\displaystyle \cos \angle A_1B_1C = \cos \angle A_1B_1M = \frac{B_1A_1}{B_1C} = \frac{\sqrt{33}}{7}.\)
Найдём \(A_1M\) из \( \triangle A_1B_1M\) по теореме косинусов.
\(A_1M^2 = A_1B_1 \, ^2 + B_1M^2 - 2A_1B_1 \cdot B_1M \cdot \cos \angle A_1B_1M;\)
\(\displaystyle A_1M^2 = 9 \cdot 33 + 28^2 - \frac{2 \cdot 28 \cdot 3 \sqrt{33} \cdot \sqrt{33}}{7} = 28^2 - 15\cdot 33 = 784 - 495 = 289;\)
\(CD = A_1M = 17.\)
Ответ: 17.
Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.
3. На сторонах прямоугольного треугольника \(ABC\) с прямым углом \(C\) построены во внешнюю сторону квадраты \(ABB_1A_1, \, ACC_1A_2\) и \(BCC_2B_2.\) Докажите, что:
а) Прямые \(AB_2\) и \(A_2B\) отсекают от катетов треугольника \(ABC\) равные отрезки.
б) Прямые \(AB_2, \, A_2B\) и высота треугольника \(ABC,\) проведённая из вершины \(C,\) пересекаются в одной точке.
Пункт (а) доказывается легко.
а) Пусть \(AB_2 \cap BC=E,\)
\(BA_2 \cap AC=F.\)
Докажем, что \(CE=CF.\)
Обозначим \(BC=a, \, AC=b.\)
\(\triangle FBC \sim \triangle A_2BC_1\) по 2 углам,
\(\displaystyle \frac{FC}{A_2C_1}=\frac{BC}{BC_1}\), так как \(A_2C_1=AC=b,\)
\(BC_1=BC+CC_1=a+b,\) получим:
\(\displaystyle \frac{FC}{b}=\frac{a}{a+b}. \,\) (1)
\(\triangle ACE \sim \triangle AC_2B_2\) по 2 углам,
\(\displaystyle \frac{CE}{C_2B_2}=\frac{AC}{AC_2}; \, \, \frac{CE}{a}=\frac{b}{a+b}. \,\) (2)
\(\displaystyle \frac{FC \cdot a}{CE \cdot b} = \frac{a}{b}, \;\) отсюда \(FC=CE.\)
Решим пункт (б) с помощью теоремы Чевы:
Запишем, чему равны длины отрезков \(AH, \; HB, \; BE, \; CE, \; CF, \; AF.\) Для длин \(AH\) и \(HB\) воспользуемся тем, что в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
\(\displaystyle AH = \frac{b^2}{\sqrt{a^2 + b^2}};\)
\(\displaystyle HB = \frac{a^2}{\sqrt{a^2 + b^2}};\)
\(\displaystyle BE = a - \frac{ab}{a+b};\)
\(\displaystyle CE = \frac{ab}{a+b};\)
\(\displaystyle CF = \frac{ab}{a+b};\)
\(\displaystyle AF = b - \frac{ab}{a+b}.\)
Проверим выполнение равенства:
\(\displaystyle \frac{AH}{HB} \cdot \frac{BE}{CE} \cdot \frac{CF}{AF} = 1.\)
\(\displaystyle \frac{\frac{b^2}{\sqrt{a^2+b^2}}}{\frac{a^2}{\sqrt{a^2+b^2}}} \cdot \frac{a - \frac{ab}{a+b}}{\frac{ab}{a+b}} \cdot \frac{\frac{ab}{a+b}}{b - \frac{ab}{a+b}} = 1.\)
Равенство выполняется.
Согласно теореме Чевы, это значит, что \(AE, \, BF\) и \(CK\) пересекаются в одной точке.
А вот как решается эта задача без теоремы Чевы, с помощью векторов:
Смотрите решение: Задача на доказательство.
Математик Менелай Александрийский жил в I веке до нашей эры (Древний Рим).
Математик и инженер Джованни Чева – XVII век, Италия.
Как видим, теоремы Менелая и Чевы оказываются полезны в некоторых задачах. Очень хорошо, если вы знаете эти теоремы. Однако если они для вас непривычны, можно применить простой школьный прием – пары подобных треугольников.