Условие задачи
а) Решите уравнение \(\left(\sqrt{2}{{sin}^2 x}+{cos x}-\sqrt{2}\right)\sqrt{-6{sin x}}=0.\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[2\pi ;\displaystyle \frac{7\pi }{2}\right].\)
Решение
а) \(\left(\sqrt{2}{{sin}^2 x}+{cos x}-\sqrt{2}\right)\sqrt{-6{sin x}}=0.\)
\(\left(\sqrt{2}\left({{sin}^2 x}-1\right)+{cos x}\right)\sqrt{-6{sin x}}=0,\)
\(\left({cos x}-\sqrt{2}{{cos}^2 x}\right)\sqrt{-6{sin x}}=0,\)
\({cos x}\left(1-\sqrt{2}{cos x}\right)\sqrt{-6{sin x}}=0.\)
Уравнение преобразуется в равносильную систему
\(\left\{ \begin{array}{c}
{sin x}\leq 0, \\
\left[ \begin{array}{c}
{sin x}=0, \\
{cos x}=0, \\
1-\sqrt{2}{cos x}=0 \end{array}
\right. \end{array}
\right.\Leftrightarrow \left\{ \begin{array}{c}
{sin x}\leq 0, \\
\left[ \begin{array}{c}
{sin x}=0, \\
{cos x}=0, \\
{cos x}=\displaystyle \frac{\sqrt{2}}{2}. \end{array}
\right. \end{array}
\right.\)
Изобразим тригонометрический круг и на нём отметим точки, соответствующие найденным значениям синуса и косинусов.
С учётом ограничения \({sin x}\le 0\) получаем серии решений:
\(\displaystyle \left[ \begin{array}{c}
x=\pi n, \; n\in Z, \\
x=-\displaystyle \frac{\pi }{2}+2\pi k, \; k\in Z, \\
x=-\displaystyle \frac{\pi }{4}+2\pi m, \; m\in Z. \end{array}
\right.\)
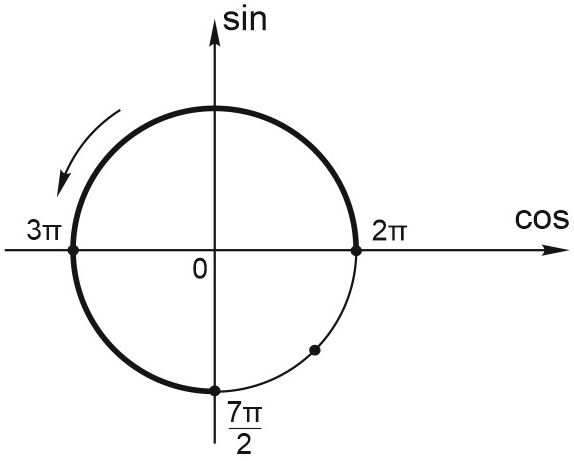
б) С помощью тригонометрического круга отберём корни, принадлежащие отрезку \(\displaystyle \left[2\pi ;\frac{7\pi }{2}\right].\) Получаем точки \(\displaystyle 2\pi ;3\pi ;\frac{7\pi }{2}.\)
Ответ:
а) \(\displaystyle x=\pi n, \; n\in Z;\;x=-\frac{\pi }{2}+2\pi k, \; k\in Z;\;x=-\frac{\pi }{4}+2\pi m,\; m\in Z;\)
б) \(\displaystyle 2\pi ; \; 3\pi ; \;\frac{7\pi }{2}.\)































