Условие задачи
В треугольнике \(ABC\) проведена биссектриса \(BK.\)
а) Докажите, что \(\displaystyle \frac{AK}{AB}=\frac{CK}{BC}.\)
б) Найдите площадь треугольника \(ABC\), если \(AB =13, \; BC = 7\) и \(\displaystyle BK=\frac{7\sqrt{13}}{4}.\)
Решение
а) Пусть \(\angle CBK=\angle ABK=\varphi ,\) а \(BK=l,\) тогда \(\displaystyle S_{\triangle CBK}=\frac{1}{2}BC\cdot l{sin \varphi }, \; S_{\triangle ABK}=\frac{1}{2}AB\cdot l{sin \varphi },\) и отношение \(\displaystyle \frac{S_{\triangle CBK}}{S_{\triangle ABK}}=\frac{BC}{AB}.\)
С другой стороны, у них общая высота \(BH\), поэтому \(\displaystyle S_{\triangle CBK}=\frac{1}{2}CK\cdot BH, \; S_{\triangle ABK}=\frac{1}{2}AK\cdot BH,\) и отношение \(\displaystyle \frac{S_{\triangle CBK}}{S_{\triangle ABK}}=\frac{CK}{AK}, \; \displaystyle \frac{BC}{AB}=\frac{CK}{AK}\) или \(\displaystyle \frac{AK}{AB}=\frac{CK}{BC},\) что и требовалось доказать.
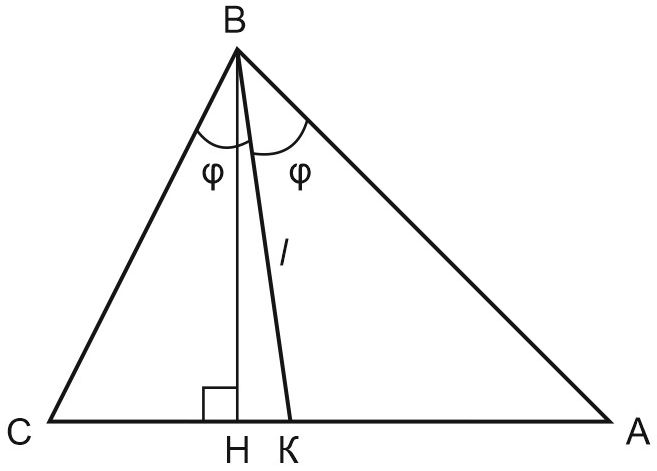
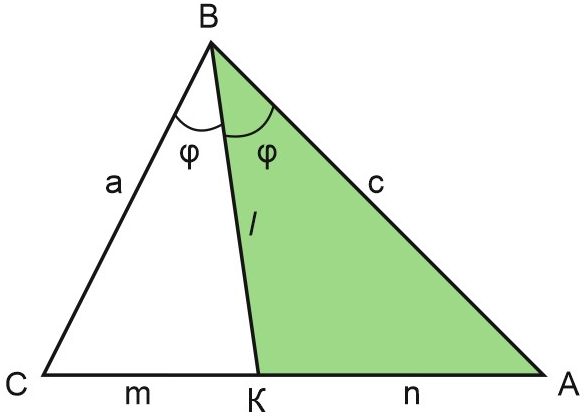
б) Выведем формулу для длины биссектрисы, используя свойство, доказанное в (а).
Пусть \(BC=a, \; AB=c, \; CK=m, \; AK=n.\)
По теореме косинусов для \(\triangle CBK\) получим \(m^2=a^2+l^2-2al{cos \varphi }.\)
А по теореме косинусов для \(\triangle ABK\) получим \(n^2=c^2+l^2-2cl{cos \varphi }.\)
Так как \(\displaystyle \frac{m^2}{n^2}=\frac{a^2}{c^2}\) (см. (а)), то \(\displaystyle \frac{a^2+l^2-2al{cos \varphi }}{c^2+l^2-2cl{cos \varphi }}=\frac{a^2}{c^2},\) откуда получаем
\(a^2c^2+a^2l^2-2a^2cl{cos \varphi }=a^2c^2+c^2l^2-2alc^2{cos \varphi }\) или
\(l^2\left(a^2-c^2\right)=2acl{cos \varphi }\left(a-c\right),\)
\(l^2\left(a+c\right)\left(a-c\right)=2acl{cos \varphi }\left(a-c\right).\)
Так как \(l\neq 0, \; a\neq c,\) то сокращая, получим \(l=\displaystyle \frac{2ac{cos \varphi }}{a+c}.\)
Подставляя данные задачи в формулу, получим \(\displaystyle \frac{7\sqrt{13}}{4}=\frac{2\cdot 7\cdot 13{cos \varphi }}{20},\) откуда \(\displaystyle {cos \varphi }=\frac{20\sqrt{13}}{4\cdot 2\cdot 13}=\frac{5}{2\sqrt{13}}=\frac{5}{\sqrt{52}}.\)
Так как угол \(\varphi \) острый, то \(\displaystyle {sin \varphi }=\sqrt{1-\frac{25}{52}}=\frac{\sqrt{27}}{2\sqrt{13}}=\frac{3\sqrt{3}}{2\sqrt{13}}.\)
Зная \({sin \varphi },\) найдём площадь \(\triangle ABK\).
\(\displaystyle S_{\triangle ABK}=\frac{1}{2}AB\cdot BK{sin \varphi }=\frac{1}{2}\cdot 13\cdot \frac{7\sqrt{13}}{4}\cdot \frac{3\sqrt{3}}{2\sqrt{13}}=\frac{39\cdot 7\sqrt{3}}{16}.\)
Площадь \(\triangle CBK\) найдём из отношения \(\displaystyle \frac{S_{\triangle CBK}}{S_{\triangle ABK}}=\frac{BC}{AB}=\frac{7}{13}, \; S_{\triangle CBK}=\frac{7}{13}\cdot S_{\triangle ABK}=\frac{49\cdot 3\sqrt{3}}{16}.\)
Тогда \(\displaystyle S_{\triangle ABC}=S_{\triangle ABK}+S_{\triangle CBK}=\frac{39\cdot 7\sqrt{3}}{16}+\frac{49\cdot 3\sqrt{3}}{16}=\frac{3\cdot 7\sqrt{3}\left(13+7\right)}{16}=\frac{105\sqrt{3}}{4}.\)
Ответ:
б) \(\displaystyle \frac{105\sqrt{3}}{4}.\)






























