Условие задачи
Решите неравенство: \(\displaystyle \frac{x^2-3x-2}{x^2-3x+2}+\frac{x^2-3x+16}{x^2-3x}\geq 0.\)
Решение
\(\displaystyle \frac{x^2-3x-2}{x^2-3x+2}+\frac{x^2-3x+16}{x^2-3x}\ge 0.\)
Делаем замену: \(t=x^2-3x,\)
\(\displaystyle \frac{t-2}{t+2}+\frac{t+16}{t}\ge 0,\) приводим к общему знаменателю \(\displaystyle \frac{2t^2+16t+32}{t\left(t+2\right)}\ge 0\) и делим на \(2>0.\)
Получаем неравенство \(\displaystyle \frac{t^2+8t+16}{t\left(t+2\right)}\geq 0 \ \Leftrightarrow \ \frac{{\left(t+4\right)}^2}{t\left(t+2\right)}\geq 0,\) которое решаем методом интервалов.
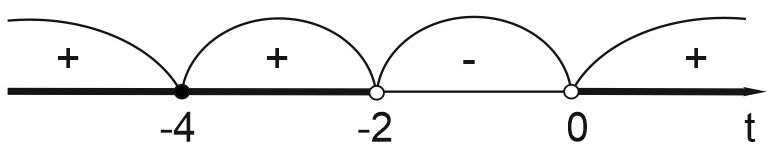
Выписываем решение \(t\in \left(-\infty ;-2\right)\cup \left(0;+\infty \right) \ \Leftrightarrow \ \left[ \begin{array}{c}
t< 2, \\
t> 0. \end{array}
\right.\)
Возвращаемся к переменной \(x\):
\(\left[ \begin{array}{c}
x^2-3x< -2, \\
x^2-3x> 0; \end{array}
\right. \ \Leftrightarrow \ \left[ \begin{array}{c}
x^2-3x+2< 0, \\
x\left(x-3\right)>0; \end{array}
\right. \ \Leftrightarrow \ \left[ \begin{array}{c}
\left(x-1\right)\left(x-2\right)< 0, \\
x\left(x-3\right)> 0. \end{array}
\right.\)
Изображаем решения неравенств на числовой оси
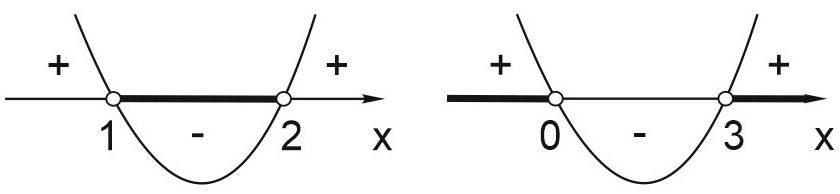
и объединяем полученные решения \(x\in \left(-\infty ;0\right)\cup \left(1;2\right)\cup \left(3;+\infty \right).\)
Ответ:
\(x\in \left(-\infty ;0\right)\cup \left(1;2\right)\cup \left(3;+\infty \right).\)






























