Условие задачи
Найдите все значения \(a\), при каждом из которых уравнение \(\displaystyle 4\left(ax-x^2\right)+\frac{1}{ax-x^2}+4=0\) имеет ровно 2 различных корня на промежутке \(\left[-1;1\right).\)
Решение
\(\displaystyle 4\left(ax-x^2\right)+\frac{1}{ax-x^2}+4=0.\)
Замена \(ax-x^2=t\) приводит к уравнению:
\(\displaystyle 4t+\frac{1}{t}+4=0 \ \Leftrightarrow \ \left\{ \begin{array}{c}
4t^2+4t+1=0, \\
t\neq 0; \end{array}
\right. \ \Leftrightarrow \ \left\{ \begin{array}{c}
{\left(2t+1\right)}^2=0, \\
t\neq 0; \end{array}
\right. \ \Leftrightarrow \ t=-\frac{1}{2}.\)
Возвращаемся к старой переменной:
\(\displaystyle ax-x^2=-\frac{1}{2} \ \Leftrightarrow \ 2ax-2x^2+1=0 \ \Leftrightarrow \ 2x^2-2ax-1=0.\)
\(D={\left(2a\right)}^2-4\cdot 2\cdot \left(-1\right)=4a^2+8>0,\) значит, уравнение имеет при любом \(a\) два различных корня.
Введём функцию \(f\left(x\right)=2x^2-2ax-1.\)
Её графиком является парабола с ветвями вверх, пересекающая ось \(Ox\) в двух различных точках, причём, \(f\left(0\right)=-1.\)
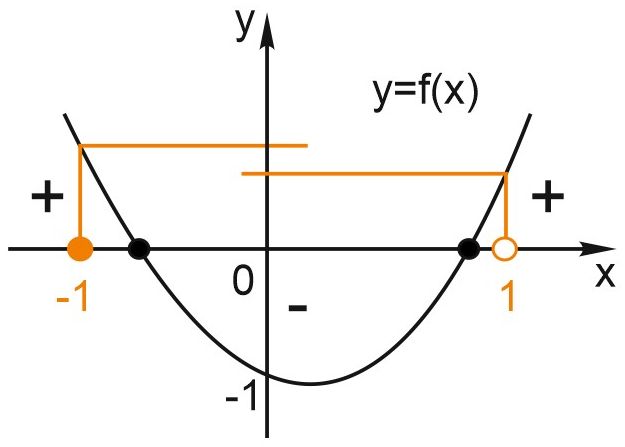
В этом случае для того, чтобы корни попадали в указанный промежуток, необходимо и достаточно, чтобы выполнялись условия:
\(\displaystyle \left\{ \begin{array}{c}
f\left(-1\right)\geq 0, \\
f\left(1\right)> 0; \end{array}
\right. \ \Leftrightarrow \ \left\{ \begin{array}{c}
2{\left(-1\right)}^2-2a\left(-1\right)-1\geq 0, \\
2-2a-1> 0; \end{array}
\right. \ \Leftrightarrow \ \left\{ \begin{array}{c}
1+2a\geq 0, \\
1-2a> 0; \end{array}
\right. \ \Leftrightarrow \ -\frac{1}{2}\leq a< \frac{1}{2}.\)
И это ответ \(a\in \left[-\displaystyle \frac{1}{2};\frac{1}{2}\right).\)
Ответ:
\(\displaystyle a\in \left[-\frac{1}{2};\frac{1}{2}\right).\)




























